¿Qué es la Distribución Muestral? (tipos, fórmulas y ejemplos)

En este artículo se explica qué es la distribución muestral en estadística y para qué sirve. Así pues, encontrarás el significado de una distribución muestral, un ejemplo resuelto de una distribución muestral y, además, las fórmulas de los tipos de distribuciones muestrales más frecuentes.

Índice

¿Qué es la distribución muestral?

La distribución muestral, o distribución de muestreo, es la distribución que resulta de considerar todas las muestras posibles de una población. Es decir, la distribución muestral es aquella distribución que se obtiene al calcular un parámetro muestral de todas las muestras posibles de una población.

Por ejemplo, si de una población estadística extraemos todas las muestras posibles y calculamos la media de cada muestra, el conjunto de medias muestrales forman una distribución muestral. En concreto, como el parámetro calculado es la media aritmética, se trata de la distribución muestral de la media.

En estadística, la distribución muestral sirve para calcular la probabilidad que se tiene de acercarse al valor del parámetro poblacional al estudiar una sola muestra. Asimismo, la distribución muestral permite estimar el error muestral para un tamaño de muestra dado.

Ejemplo de la distribución muestral

Ahora que ya sabemos la definición de la distribución muestral, vamos a ver un ejemplo simple para acabar de entender el concepto.

En una caja metemos tres bolas y cada una tiene escrito un número del uno al tres, de manera que una bola tiene el número 1, otra bola tiene el número 2 y la última bola tiene el número 3. Para un tamaño muestral n=2, calcula las probabilidades de la distribución muestral de la media si se seleccionan las muestras con reemplazo.

Las muestras se seleccionan con reemplazo, es decir, la bola que se coge para seleccionar el primer elemento de la muestra se vuelve a meter dentro de la caja y puede volver a ser seleccionada en la segunda extracción. Por lo tanto, todas las muestras posibles de la población son:

1,1   1,2   1,3
2,1   2,2   2,3
3,1   3,2   3,3

Así pues, calculamos la media aritmética de cada muestra posible:

$(1,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{11}=\cfrac{1+1}{2}=1$

$(1,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{12}=\cfrac{1+2}{2}=1,5$

$(1,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{13}=\cfrac{1+3}{2}=2$

$(2,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{21}=\cfrac{2+1}{2}=1,5$

$(2,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{22}=\cfrac{2+2}{2}=2$

$(2,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{23}=\cfrac{2+3}{2}=2,5$

$(3,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{31}=\cfrac{3+1}{2}=2$

$(3,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{32}=\cfrac{3+2}{2}=2,5$

$(3,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{33}=\cfrac{3+3}{2}=3$

Por lo tanto, las probabilidades de obtener cada valor de la media muestral al seleccionar una muestra aleatoria de la población son las siguientes:

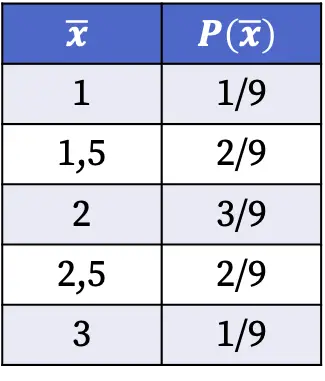
tabla del ejemplo de la distribución muestral

Las probabilidades de la distribución muestral que se muestran en la tabla anterior se han calculado dividiendo el número de muestras que tienen dicho valor de la media entre el número total de casos posibles. Por ejemplo: la media muestral vale 1,5 en dos casos de los nueve posibles, por lo tanto, P(1,5)=2/9.

Tipos de distribuciones muestrales

Las distribuciones muestrales (o distribuciones de muestreo) se pueden clasificar según el parámetro muestral a partir del cual se han obtenido. Así pues, los tipos de distribuciones más usuales son los siguientes:

Distribución muestral de la media: es la distribución muestral que resulta de calcular la media aritmética de cada muestra.
Distribución muestral de la proporción: es la distribución muestral que se obtiene al calcular la proporción de todas las muestras.

Distribución muestral de la varianza: es la distribución muestral que forman el conjunto de todas las varianzas muestrales.
Distribución muestral de la diferencia de medias: es la distribución muestral que resulta de calcular la diferencia entre las medias de todas las muestras posibles de dos poblaciones diferentes.
Distribución muestral de la diferencia de proporciones: es la distribución muestral que se consigue al restar todas las proporciones muestrales posibles de dos poblaciones.

A continuación se explica cada tipo de distribución muestral más detalladamente.

Distribución muestral de la media

Dada una población que sigue una distribución de probabilidad normal de media $\mu$ y desviación estándar $\sigma$ y se extraen de ella muestras de tamaño $n$ , la distribución muestral de la media también estará definida por una distribución normal con las siguientes características:

$\begin{array}{c}\mu_{\overline{x}}=\mu \qquad \sigma_{\overline{x}}=\cfrac{\sigma}{\sqrt{n}}\\[4ex]\displaystyle N_{\overline{x}}\left(\mu, \frac{\sigma}{\sqrt{n}}\right) \end{array}$

Donde $\mu_{\overline{x}}$ es la media de la distribución muestral de la media y $\sigma_{\overline{x}}$ es su desviación típica. Asimismo, $\cfrac{\sigma}{\sqrt{n}}$ es el error estándar de la distribución muestral.

Nota: si la población no sigue una distribución normal pero el tamaño muestral es grande (n>30), la distribución muestral de la media también se puede aproximar a la distribución normal anterior por el teorema central del límite.

Por lo tanto, como la distribución muestral de la media sigue una distribución normal, la fórmula para calcular cualquier probabilidad relacionada con la media de una muestra es la siguiente:

$Z=\cfrac{\overline{x}-\mu}{\displaystyle\frac{\sigma}{\sqrt{n}}}$

Donde:

$\overline{x}$ es la media de la muestra.

$\mu$ es la media de la población.
$s$ es la desviación típica de la población.
$n$ es el tamaño de la muestra.

$Z$ es una variable definida por la distribución normal estándar N(0,1).

➤ Ver: Ejercicio resuelto de la distribución muestral de la media

Distribución muestral de la proporción

En realidad, al estudiar una proporción de una muestra estamos analizando los casos de éxito, por lo tanto, la variable aleatoria del estudio sigue una distribución de probabilidad binomial.

Según el teorema central del límite, para tamaños grandes (n>30) podemos aproximar una distribución binomial a una distribución normal. Por lo tanto, la distribución muestral de la proporción se aproxima a una distribución normal con los siguientes parámetros:

$\begin{array}{c}\displaystyle\mu_{p}=p \qquad \sigma_{p}=\sqrt{\frac{pq}{n}}\\[4ex]\displaystyle N_{p}\left(p, \sqrt{\frac{pq}{n}}\right) \end{array}$

Donde $p$ es la probabilidad de éxito y $q$ es la probabilidad de fracaso $q=1-p$ .

Nota: una distribución binomial solo se puede aproximar a una distribución normal si $n>30$ , $np\ge 5$ y $nq\ge 5$ .

Por lo tanto, como se puede aproximar la distribución muestral de la proporción a una distribución normal, la fórmula para calcular cualquier probabilidad relacionada con la proporción de una muestra es la siguiente:

$Z=\cfrac{\widehat{p}-p}{\displaystyle\sqrt{\frac{pq}{n}}}$

Donde:

$\widehat{p}$ es la proporción de la muestra.
$p$ es la proporción de la población.

$q$ es la probabilidad de fracaso de la población, $q=1-p$ .
$n$ es el tamaño de la muestra.
$Z$ es una variable definida por la distribución normal estándar N(0,1).

➤ Ver: Ejercicio resuelto de la distribución muestral de la proporción

Distribución muestral de la varianza

La distribución muestral de la varianza está definida por la distribución de probabilidad chi-cuadrado. Por lo tanto, la fórmula del estadístico de la distribución muestral de la varianza es la siguiente:

$\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

Donde:

$\chi^2$ es el estadístico de la distribución muestral de la varianza, el cual sigue una distribución chi-cuadrado.
$n$ es el tamaño muestral.

$s^2$ es la varianza de la muestra.
$\sigma^2$ es la varianza de la población.

➤ Ver: Ejercicio resuelto de la distribución muestral de la varianza

Distribución muestral de la diferencia de medias

Si el tamaño muestral es suficientemente grande (n₁≥30 y n₂≥30), la distribución muestral de la diferencia de medias sigue una distribución normal. En concreto, los parámetros de dicha distribución se calculan de la siguiente manera:

$\begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}$

Nota: si las dos poblaciones son distribuciones normales, entonces la distribución muestral de la diferencia de medias sigue una distribución normal independientemente de los tamaños muestrales.

Por lo tanto, como la distribución muestral de la diferencia de medias está definida por una distribución normal, la fórmula para calcular el estadístico de la distribución muestral de la diferencia de medias es la siguiente:

$Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

Donde:

$\overline{x_i}$ es la media de la muestra i.
$\mu_i$ es la media de la población i.
$\sigma_i$ es la desviación estándar de la población i.

$n_i$ es el tamaño de la muestra i.
$Z$ es una variable definida por la distribución normal estándar N(0,1).

Fíjate que las muestras de las poblaciones diferentes pueden tener un tamaño muestral distinto.

➤ Ver: Ejercicio resuelto de la distribución muestral de la diferencia de medias

Distribución muestral de la diferencia de proporciones

Las muestras que se seleccionan para la distribución muestral de la diferencia de proporciones están definidas por distribuciones binomiales, ya que a efectos prácticos una proporción es una relación de los casos de éxito respecto al número total de observaciones.

No obstante, debido al teorema del límite central, las distribuciones binomiales se pueden aproximar a distribuciones de probabilidad normales. En consecuencia, la distribución muestral de la diferencia de proporciones se puede aproximar a una distribución normal con las siguientes características:

$\begin{array}{c}\displaystyle\mu_{\widehat{p_1}-\widehat{p_2}}=p_1-p_2 \qquad \sigma_{\widehat{p_1}-\widehat{p_2}}=\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\\[6ex]\displaystyle N_{p}\left(p_1-p_2, \sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\right) \end{array}$

Nota: la distribución muestral de la diferencia de proporciones solo se puede aproximar a una distribución normal si $n_1\geq30$ , $n_2\geq 30$ , $n_1p_1\geq5$ , $n_2p_2\geq5$ , $n_1q_1\geq5$ y $n_2q_2\geq5$ .

Por lo tanto, como se puede aproximar la distribución muestral de la diferencia de proporciones a una distribución normal, la fórmula para calcular el estadístico de la distribución muestral de la diferencia de proporciones es la siguiente:

$Z=\cfrac{(\widehat{p_1}-\widehat{p_2})-(p_1-p_2)}{\displaystyle\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}}$

Donde:

$\widehat{p_i}$ es la proporción de la muestra i.

$p_i$ es la proporción de la población i.
$q_i$ es la probabilidad de fracaso de la población i, $q_i=1-p_i$ .
$n_i$ es el tamaño de la muestra i.

$Z$ es una variable definida por la distribución normal estándar N(0,1).

➤ Ver: Ejercicio resuelto de la distribución muestral de la diferencia de proporciones

6 comentarios en “Distribución muestral”

Ma-link
15/08/2023 a las 22:34

Excelente exposición. Precisa y concisa

Responder
1. Probabilidad y Estadística
  20/08/2023 a las 11:28
  
  ¡Muchas gracias!
Miriam Ruiz
07/10/2023 a las 16:40

Amo esta página, explica todo muy bien y conciso. Sirve para consultar en todo momento.

Responder
1. Probabilidad y Estadística
  14/10/2023 a las 11:40
  
  ¡Muchas gracias Miriam! ¡Me alegro de que te resulte útil!
Gustavo Vallenilla
27/11/2023 a las 17:27

Excelentísimo, trabajo, soy licenciado en estadística y hacen algo muy bueno para los estudiantes.

Responder
1. Probabilidad y Estadística
  05/12/2023 a las 20:06
  
  ¡Gracias Gustavo! ¡Me alegra que te guste!