Frecuencia relativa acumulada

En este post se explica en qué consiste la frecuencia relativa acumulada en estadística. Así pues, encontrarás la definición de frecuencia relativa acumulada, cómo sacar la frecuencia relativa acumulada y dos ejercicios resueltos paso a paso.

¿Qué es la frecuencia relativa acumulada?

En estadística, la frecuencia relativa acumulada es la suma acumulativa de las frecuencias relativas. Es decir, la frecuencia relativa acumulada de un valor es igual a la frecuencia relativa de dicho valor más las frecuencias relativas de todos los valores menores que él.

El símbolo de la frecuencia relativa acumulada es H_i. Sin embargo, en estadística aún no existe un consenso completo respecto al símbolo de este tipo de frecuencia, por lo que puede que también la encuentres expresada utilizando otro símbolo.

Evidentemente, para entender el significado de frecuencia relativa acumulada primero debes tener claro el concepto de frecuencia relativa, por eso te recomiendo visitar el siguiente enlace antes de seguir con la explicación:

Cómo calcular la frecuencia relativa acumulada

Para calcular la frecuencia relativa acumulada se deben seguir los siguientes pasos:

1. Construir una tabla de frecuencias con todos los valores diferentes de la muestra estadística.
2. Calcular la frecuencia absoluta de cada valor.
3. A partir de las frecuencias absolutas, determinar la frecuencia relativa de cada valor.
4. Hallar la frecuencia relativa acumulada de cada valor, que se calcula sumando la frecuencia relativa del propio valor más las frecuencias relativas de todos los valores menores.

Ten en cuenta que si quieres calcular la frecuencia relativa acumulada porcentual, es decir, la frecuencia relativa acumulada expresada en forma de porcentaje, simplemente tienes que seguir los mismos pasos y multiplicar los resultados por 100.

Ejemplos de frecuencia relativa acumulada

Para que puedas ver cómo se calcula la frecuencia relativa acumulada, seguidamente se presentan dos ejemplos resueltos paso a paso. En el primer ejemplo se halla la frecuencia relativa acumulada de una variable discreta y en el segundo ejemplo de una variable continua, pues el proceso varia ligeramente.

Ejemplo 1: variable discreta

• Las notas obtenidas en la asignatura de estadística en una clase de 30 alumnos son las siguientes. ¿Cuál es la frecuencia relativa acumulada de cada nota?

En este caso la variable es discreta, pues no puede tomar un valor decimal. De manera que no es necesario agrupar los datos en intervalos, sino que podemos hacer los cálculos directamente.

Así pues, hacemos una tabla de frecuencias y determinamos la frecuencia absoluta de cada valor diferente:

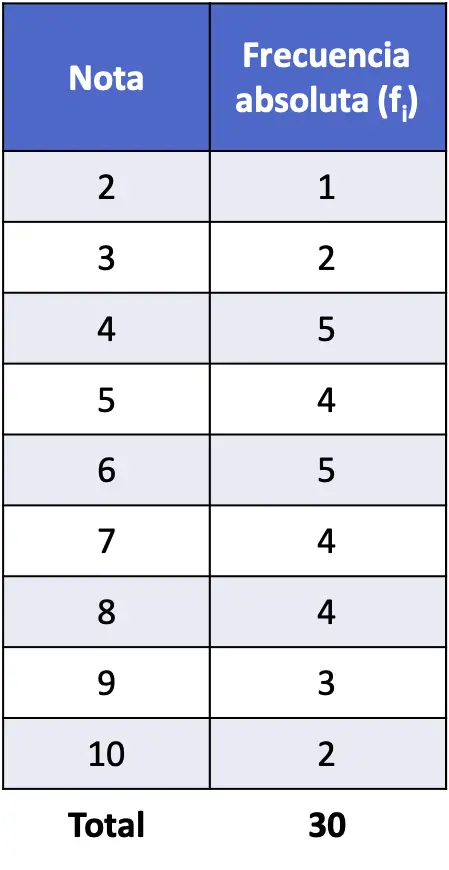
Luego, calculamos la frecuencia relativa de cada valor (puedes ver cómo se hace en el enlace del principio del post).

Y una vez hemos calculado la frecuencia absoluta y la frecuencia relativa del conjunto de datos, podemos sacar la frecuencia relativa acumulada. Para ello, tenemos que sumar la frecuencia relativa del valor en cuestión más todas las frecuencias relativas anteriores o, lo que es lo mismo, la frecuencia relativa acumulada anterior:

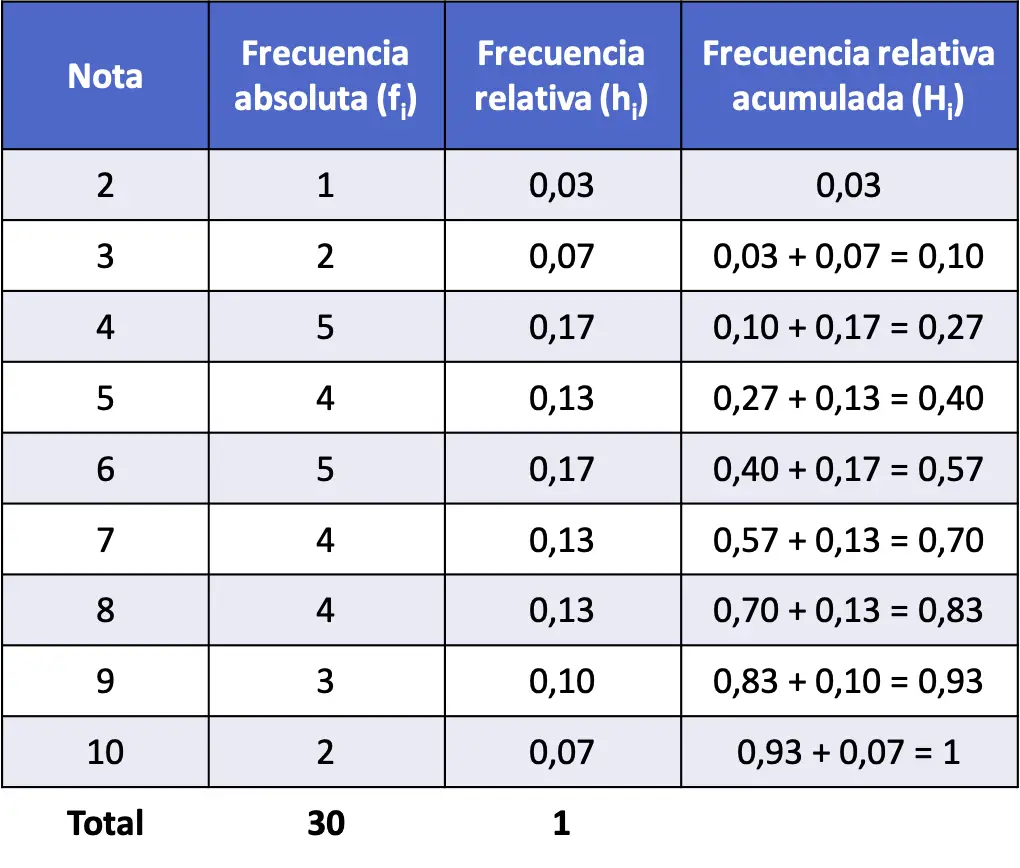
En definitiva, la tabla de frecuencias con la frecuencia absoluta, la frecuencia relativa y la frecuencia relativa acumulada es la siguiente:

Ten presente que el último valor de la frecuencia relativa acumulada siempre debe ser 1. Si obtienes cualquier otro número, significa que has cometido algún error en los cálculos.

Ejemplo 2: variable continua

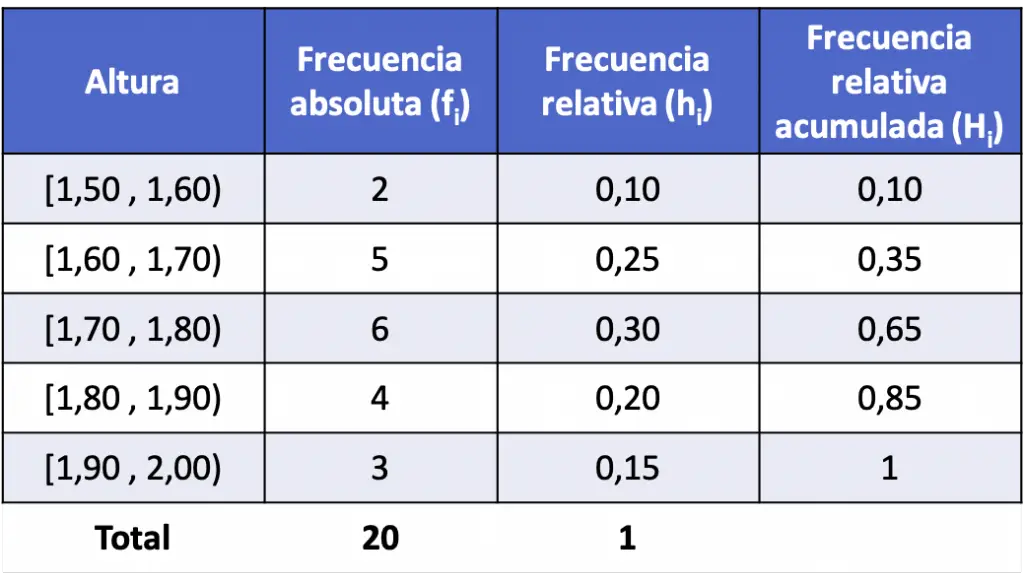
• Se ha medido la altura a 20 personas y se han obtenido los resultados anotados abajo. Separa los datos en intervalos y halla la frecuencia relativa acumulada de cada intervalo.

Este caso es diferente al problema anterior ya que los números son decimales, lo que significa que la variable puede tomar cualquier valor y, por tanto, es continua. De modo que haremos la tabla de frecuencias agrupando los datos en intervalos.

Así pues, construimos la tabla y sacamos la frecuencia absoluta de cada intervalo:

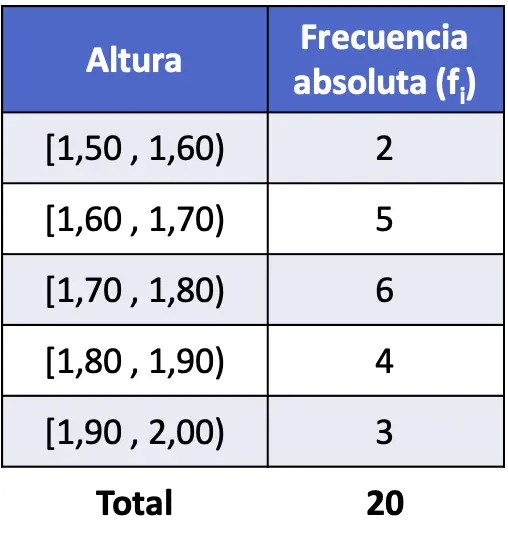
Ahora calculamos las frecuencias relativas dividiendo la frecuencia absoluta de cada intervalo entre el número total de datos:

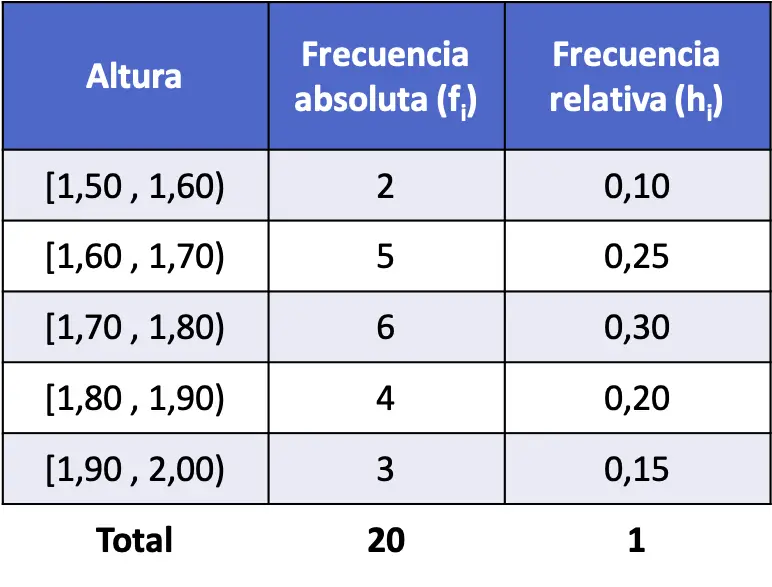
Y, finalmente, hallamos las frecuencias relativas acumuladas de todos los intervalos. Igual que antes, para determinar una frecuencia relativa acumulada de un intervalo tenemos que sumar la frecuencia relativa de dicho intervalo más las frecuencias relativas anteriores:

Frecuencia relativa acumulada y frecuencia absoluta acumulada

Acabamos de ver cómo se saca la frecuencia relativa acumulada a partir de la frecuencia relativa. Sin embargo, este tipo de frecuencia también se puede hallar utilizando la frecuencia absoluta acumulada.

La frecuencia relativa acumulada se puede calcular dividiendo la frecuencia absoluta acumulada entre el número total de datos de la muestra.

Por lo tanto, la fórmula de la frecuencia relativa acumulada es la siguiente:

Donde:

• es la frecuencia relativa acumulada.
• es la frecuencia absoluta acumulada.
• es el número total de datos.

Siguiendo el primer ejemplo resuelto arriba, a continuación se muestra cómo se halla la frecuencia relativa acumulada a partir de la frecuencia absoluta acumulada:

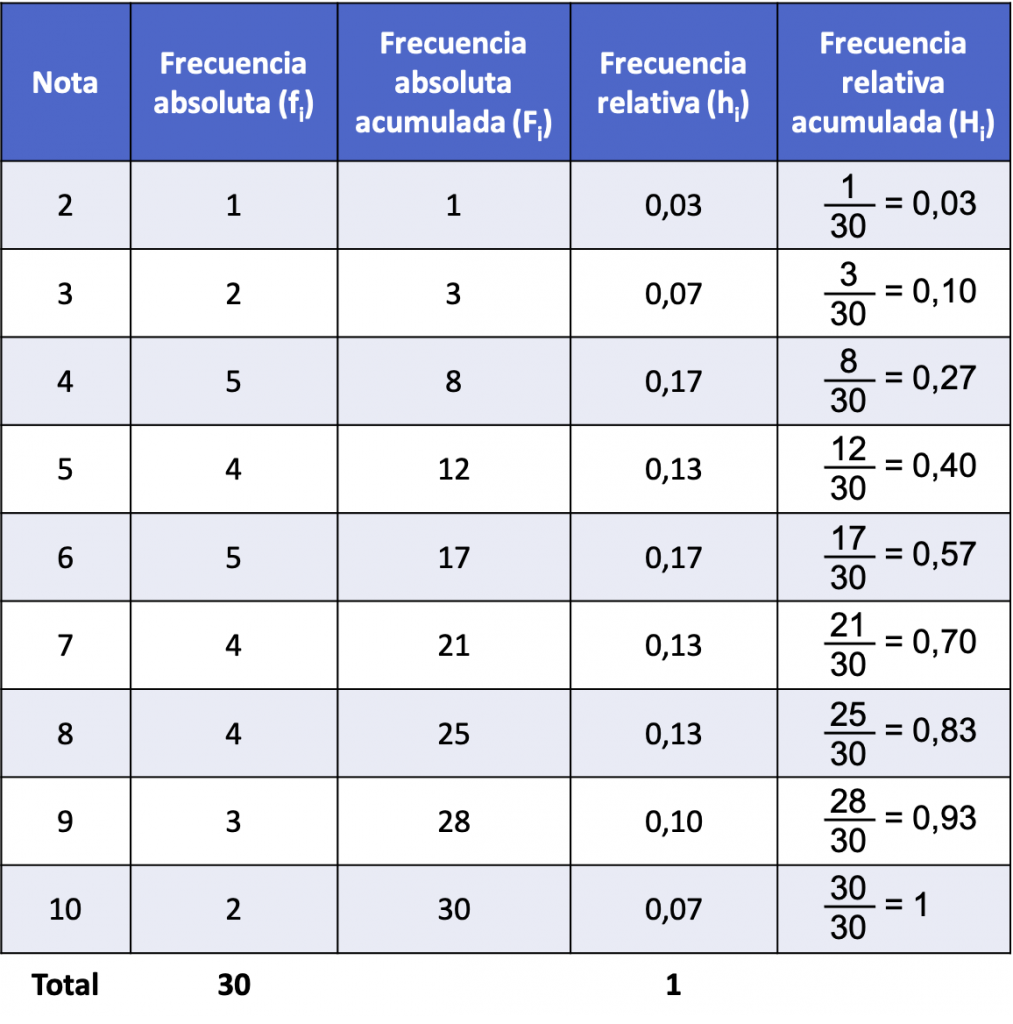
La tabla anteriore como contiene todos los tipos de frecuencias estadísticas, se llama tabla de frecuencias. Haz clic aquí para saber más al respecto: