En este artículo se explica en qué consiste un diagrama de árbol y cómo se hace. Así pues, encontrarás ejemplos de diagramas de árbol, las ventajas de este tipo de diagrama y, además, un ejercicio resuelto paso a paso.
Índice
¿Qué es un diagrama de árbol?
Un diagrama de árbol, también conocido como árbol de probabilidad, es una representación gráfica de todos los posibles resultados de un experimento junto con sus probabilidades.
De modo que un diagrama de árbol sirve para representar gráficamente todos los posibles resultados de un espacio muestral y calcular sus probabilidades.
Un diagrama de árbol se hace de manera que cada resultado (nudo) se ramifica en nuevos posibles resultados (ramas) hasta llegar a los resultados finales.
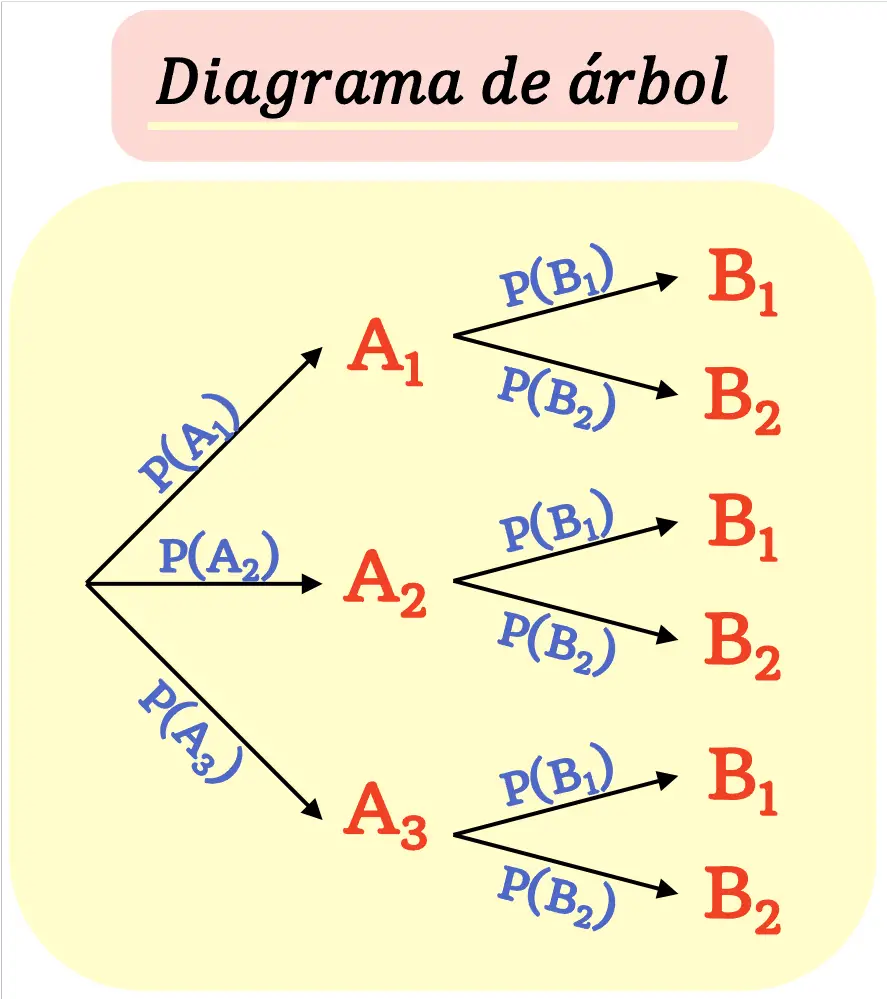
Debes tener en cuenta que la suma de las probabilidades de todas las ramas que salen de un nudo debe ser igual a 1.
Cómo hacer un diagrama de árbol
Para hacer un diagrama de árbol debes seguir los siguientes pasos:
- El primer paso para hacer un diagrama de árbol es dibujar una rama por cada resultado posible. Estas serán las ramas de primera generación.
- Luego se añade la probabilidad asociada a cada evento a su rama correspondiente.
- El final de cada rama de primera generación es un nudo del cual se deben representar las ramas de los siguientes posibles sucesos.
- Al igual que en las primeras ramas, se deben agregar las probabilidades de los sucesos representados.
- Repetir los pasos 3 y 4 hasta llegar a los nudos finales, es decir, a los posibles finales del experimento.
Cabe destacar que el número de ramas de un nivel no tiene por qué ser igual al número de ramas de un nivel diferente. Asimismo, el número de ramas que salen de un posible resultado puede variar incluso dentro de un mismo nivel.
Ejemplo de diagrama de árbol
Ahora que ya sabemos la definición y la teoría sobre cómo se hace un diagrama de árbol, vamos a ver un ejemplo resuelto paso a a paso para entender mejor el concepto.
- Construye el diagrama de árbol de probabilidades del lanzamiento de tres monedas independientes. Luego calcula la probabilidad de obtener cara en los tres lanzamientos.
En el lanzamiento de una moneda solo hay dos posibles resultados, podemos obtener cara o cruz. Por lo tanto, la probabilidad de obtener cara o cruz al lanzar una moneda es:
![]()
![]()
Una vez conocemos las probabilidades de los posibles resultados, procedemos a representar el diagrama de árbol.
Como los lanzamientos de las monedas son independientes, la probabilidad de sacar cara o cruz siempre será la misma en cada lanzamiento. Por lo tanto, para construir el diagrama de árbol se deben representar dos ramas (cara y cruz) con la misma probabilidad por cada lanzamiento que se realiza.

Y una vez hemos hecho el diagrama de árbol solo nos queda determinar la probabilidad de sacar cara en los tres lanzamientos de monedas.
Para calcular la probabilidad de un posible resultado de un diagrama de árbol se deben multiplicar las probabilidades de todas las ramas contiguas.
Por lo tanto, en este caso debemos multiplicar todas las probabilidades de obtener cara, ya que son las probabilidades del camino que nos lleva a nuestro resultado deseado.
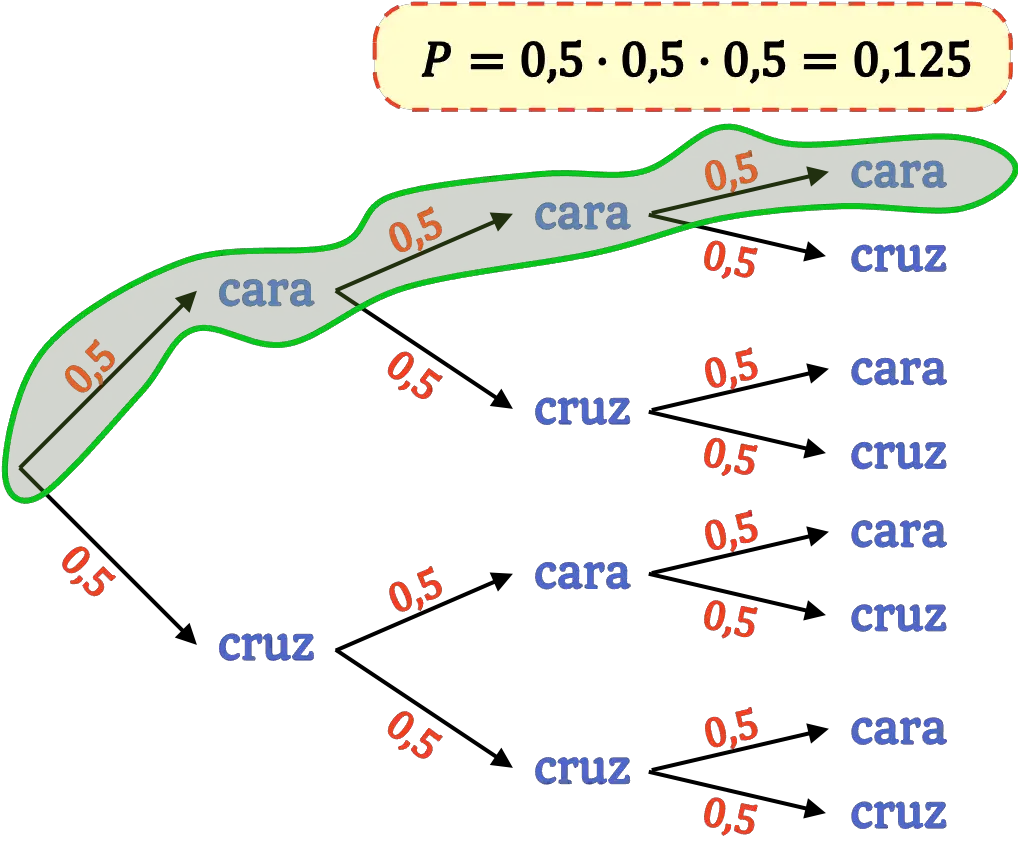
Así que la probabilidad de obtener cara en los tres lanzamientos de moneda se calcula de la siguiente manera:
![]()
En definitiva, la probabilidad de conseguir tres veces cara de manera consecutiva es del 12,5%.
Ejercicio resuelto de diagrama de árbol
En un pueblo solo hay 3 guarderías: en la guardería A van el 60% de los niños, en la guardería B el 30% y en la guardería C el 10%. Además, en las tres guarderías el 55% de las personas son chicas. Construye el diagrama de árbol y calcula las siguientes probabilidades:
- Probabilidad de que al seleccionar al azar un niño sea una chica de la guardería B.
- Probabilidad de que al seleccionar al azar un niño de cualquier guardería sea un chico.
Ten cuenta que si la proporción de chicas en todas las guarderías es del 55%, el porcentaje de chicos se calcula simplemente restando 1 menos 0,55:
![]()
Ahora que ya conocemos todas las probabilidades, podemos hacer el diagrama de árbol con las probabilidades con todas las posibilidades:
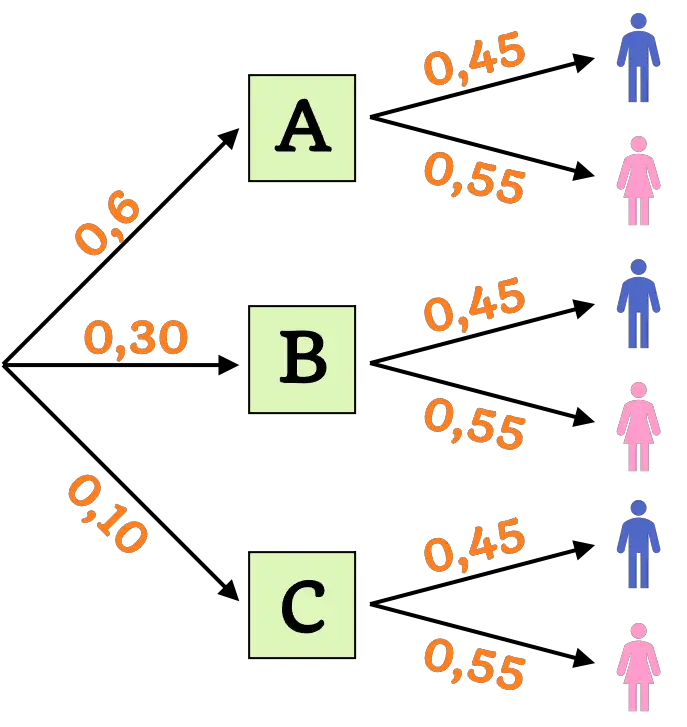
Por lo tanto, la probabilidad de seleccionar aleatoriamente una chica de la guardería B se calcula de la siguiente manera:
![]()
Por otro lado, para determinar la probabilidad de seleccionar un chico de cualquier guardería primero debemos hallar la probabilidad de escoger un chico para cada guardería y luego sumarlas:
![]()
![]()
![]()
![]()
Ventajas del diagrama de árbol
Debido a las características del diagrama de árbol, las ventajas de este tipo de gráfico estadístico son las siguientes:
- Los diagramas de árboles son muy útiles para tomar decisiones.
- Se puede representar la relación entre todos los posibles resultados de manera gráfica.
- Resulta muy práctico para encontrar la causa principal de un problema.
- Facilita la resolución de problemas de probabilidad y estadística.
- Un diagrama de árbol ayuda a organizar las ideas y a hacer un análisis de la situación.

Creo que esto es incorrecto:
Por lo tanto, la probabilidad de seleccionar aleatoriamente una chica de la guardería B se calcula de la siguiente manera:
Porque multiplican la probabilidad de B pero en el problema ya se da por supuesto que se elige alguien al azar de B.
Hola Guillermo,
Tú te refieres al cálculo de la probabilidad condicionada de que sea chica si se elige alguien de la guardería B y, efectivamente, en tal caso el cálculo de la probabilidad sería diferente (te recomiendo ver nuestro artículo de la probabilidad condicionada). Pero, aunque entiendo que puede dar a confusión, el enunciado del problema pide determinar la probabilidad de escoger una chica de la guardería B.
Gracias por ayudarme en mi tarea
¡Un placer Abraham!
gracias
tengo que exponer este tema, ¡esto fue de mucha ayuda!