En este artículo se explica qué es la distribución t de Student y para qué sirve. Además, se muestra la gráfica de la distribución t de Student y cuáles son las características de este tipo de distribución de probabilidad.
Índice
¿Qué es la distribución t de Student?
La distribución t de Student es una distribución de probabilidad muy utilizada en estadística. En concreto, la distribución t de Student se usa en la prueba t de Student para determinar la diferencia entre dos medias muestrales y para hacer intervalos de confianza.
La distribución t de Student fue desarrollada por el estadístico William Sealy Gosset en el año 1908 bajo el pseudónimo «Student».
La distribución t de Student queda definida con su número de grados de libertad, que se obtiene restando una unidad al número total de observaciones. Por lo tanto, la fórmula para determinar los grados de libertad de una distribución t de Student es ν=n-1.
![\begin{array}{c}\nu=n-1\\[2ex]X\sim t_\nu\end{array}](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-7299638a075cc6b6e1059a4e8d12a821_l3.svg "Rendered by QuickLaTeX.com")
Gráfica de la distribución t de Student
Ahora que ya sabemos la definición de la distribución t de Student, vamos a ver cuál es su gráfica. Así pues, a continuación puedes ver representadas gráficamente varios ejemplos de distribuciones t de Student con diferentes grados de libertad.
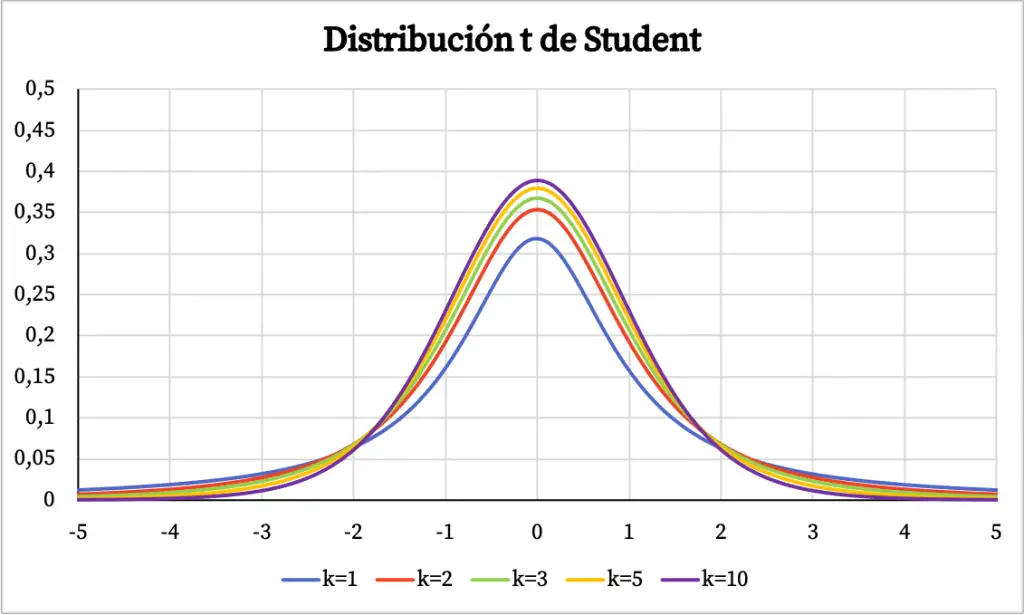
De la gráfica de la distribución t de Student se pueden deducir las siguientes propiedades:
- La distribución t de Student es simétrica centrada en el 0 y tiene forma de campana.
- La distribución t de Student es más dispersa que la distribución normal, es decir, la curva de la distribución t de Student es más ancha.
- Cuantos más grados de libertad tiene la distribución t de Student, menor es su dispersión.
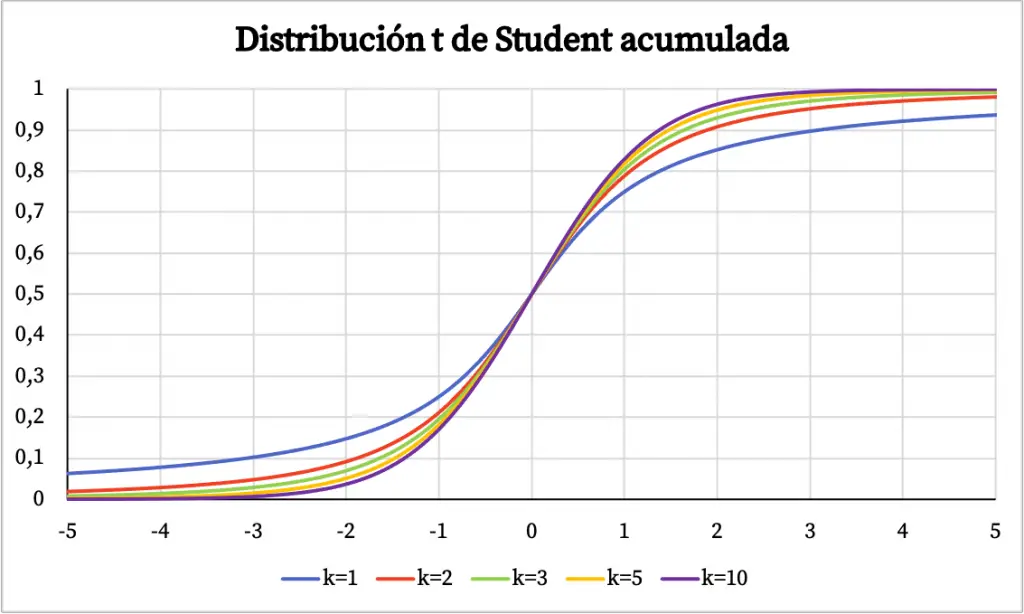
En el gráfico de arriba se ha representado la función de densidad de la distribución t de Student según sus grados de libertad. Sin embargo, abajo puedes cómo varia la función de probabilidad acumulada de la distribución t de Student:
Características de la distribución t de Student
A continuación, se muestran las características más importantes de la distribución t de Student.
- El dominio de la distribución t de Student son todos los números reales.
- Para distribuciones t de Student con más de un grado de libertad, la media de la distribución es igual a 0.
![\begin{array}{c}X\sim t_\nu\\[2ex] E[X]=0 \qquad \text{para }\nu>1\end{array}](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-d23254821795e65dcc8005d9b8f522f8_l3.svg "Rendered by QuickLaTeX.com")
- La varianza de una distribución t de Student se puede calcular mediante la siguiente expresión:
![\begin{array}{c}X\sim t_\nu\\[2ex] Var(X)=\cfrac{\nu}{\nu-2} \qquad \text{para }\nu>2\end{array}](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-dacf3b35350386e3c173030813ae68c9_l3.svg "Rendered by QuickLaTeX.com")
- La mediana y la moda de la distribución t de Student, independientemente del número de grados de libertad, siempre es 0.
![\begin{array}{c}Me=0\\[2ex]Mo=0\end{array}](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-1c51a37a1a29d5f39977c4172a4c4586_l3.svg "Rendered by QuickLaTeX.com")
- La función de densidad de la distribución t de Student queda definida mediante la siguiente fórmula:
![\displaystyle P[X=x]=\frac{\Gamma((\nu+1)/2)} {\sqrt{\nu\pi}\,\Gamma(\nu/2)} (1+x^2/\nu)^{-(\nu+1)/2}](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-6442a4ffd8a266e77a593e2f56497353_l3.svg "Rendered by QuickLaTeX.com")
- La función de distribución de probabilidad acumulada de la distribución t de Student se define con la siguiente fórmula:
![\displaystyle P[X\leq x]=\frac{1}{2} + x \Gamma \left( \frac{\nu+1}{2} \right) \cdot\frac{\,_2F_1 \left ( \frac{1}{2},\frac{\nu+1}{2};\frac{3}{2};-\frac{x^2}{\nu} \right)}{\sqrt{\pi\nu}\,\Gamma \left(\frac{\nu}{2}\right)}](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-2ebf2f785fa537a5c92e573f4dfe47a7_l3.svg "Rendered by QuickLaTeX.com")
- Para distribuciones t de Student con grados de libertad mayor que 3, el coeficiente de asimetría es nulo porque se trata de una distribución simétrica.
- Si los grados de libertad de la distribución t de Student son más que cuatro, la curtosis se puede calcular dividiendo seis entre los grados de libertad menos cuatro.
Aplicaciones de la distribución t de Student
La distribución t de Student es una distribución de probabilidad muy utilizada en estadística. De hecho, incluso existe la prueba de t de Student, la cual sirve para hacer contrastes de hipótesis e intervalos de confianza.
Así pues, la distribución t de Student permite analizar la diferencia entre dos medias muestrales, en concreto, se usa para determinar si dos muestras tienen medias significativamente distintas. Asimismo, se utiliza la prueba de la t de Student para averiguar si la recta obtenida de un análisis de regresión lineal tiene pendiente o no.
En definitiva, las aplicaciones de la distribución t de Student se basan en analizar conjuntos de datos que en teoría siguen una distribución normal pero que el número total de observaciones es demasiado pequeño como para utilizar este tipo de distribución.
MUY BUENA INFORMACIÓN
¡Muchas gracias Juan!
Buenos día. Muy buena información. Esta distribución también sirve para revisar si un proceso está o no, dentro de los parámetros establecidos, empleando diferentes niveles de confianza. Saludos