▷ Distribución Normal

En este artículo se explica qué es la distribución normal en estadística. Así pues, encontrarás la definición de la distribución normal, ejemplos de distribuciones normales y cuáles son las propiedades de la distribución normal.

Índice

¿Qué es la distribución normal?

La distribución normal es una distribución de probabilidad continua cuya gráfica tiene forma de campana y es simétrica respecto a su media. En estadística, la distribución normal sirve para modelizar fenómenos de características muy diferentes, por eso es tan importante esta distribución.

De hecho, en estadística la distribución normal se considera, por mucho, la distribución más importante de todas las distribuciones de probabilidad, ya que no solo permite modelizar un gran número de fenómenos reales, sino que además la distribución normal se puede usar para aproximar otros tipos de distribuciones bajo ciertas condiciones.

El símbolo de la distribución normal es la letra mayúscula N. Así pues, para indicar que una variable sigue una distribución normal se indica con la letra N y se añade entre paréntesis los valores de su media aritmética y su desviación estándar.

$X\sim N(\mu,\sigma)$

La distribución normal recibe muchos nombres diferentes, entre ellos destacan distribución de Gauss, distribución gaussiana y distribución de Laplace-Gauss.

Ejemplos de distribuciones normales

Normalmente, los conjuntos de datos que siguen una distribución normal tienen un gran número de observaciones y tratan de temas muy generales. A continuación puedes ver varios ejemplos de muestras estadísticas que típicamente se pueden modelar con una distribución normal.

Ejemplos de la distribución de normal:

La estatura de los alumnos de un curso.
El coeficiente intelectual de los trabajadores de una empresa.
El número de piezas defectuosas producidas en una fábrica durante un día.
Las notas obtenidas en un examen por los alumnos de un curso.
La rentabilidad de las acciones de las empresas que cotizan en bolsa.

Gráfica de la distribución normal

Una vez hemos visto en qué consiste la distribución normal y varios ejemplos de este tipo de distribución de probabilidad, vamos a ver cómo es su gráfica para entender mejor el concepto.

En el siguiente gráfico puedes ver cómo varia la función de densidad de la distribución normal dependiendo de los valores de su media aritmética y de su desviación típica.

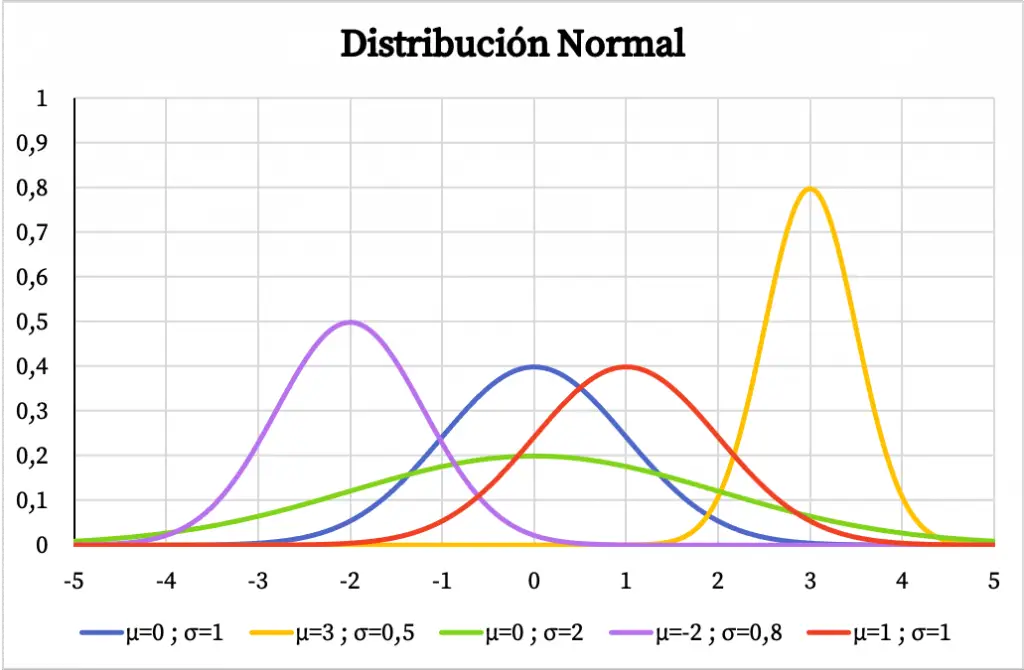
Al tener forma de campana centrada en la media aritmética, si una variable tiene una distribución normal significa que el valor más repetido es la media y que los valores alrededor de la media se repiten con más frecuencia que los valores de los extremos. Asimismo, cuanto mayor sea la desviación típica de la distribución normal, más aplastada es la forma de su representación gráfica.

Por otro lado, la gráfica de la función de probabilidad acumulada de la distribución normal también depende de los valores de su media aritmética y su desviación típica, tal y como puedes ver en la siguiente imagen:

La función de densidad y la función de distribución de la distribución normal permiten calcular probabilidades relacionadas con esta distribución. No obstante, en lugar de utilizar sus fórmulas, puedes usar directamente las tablas de la distribución normal ya que es más rápido. Puedes ver estas tablas en el siguiente enlace:

➤ Ver: Tabla de la distribución normal

Características de la distribución normal

La distribución normal tiene las siguientes características:

La distribución normal depende de dos parámetros característicos que son su media aritmética (μ) y su desviación típica (σ).

$X\sim N(\mu,\sigma)$

La distribución normal puede tomar tanto valores positivos como negativos, por lo tanto, el dominio de la distribución normal son todos los números reales.

$x\in \mathbb{R}$

La mediana y la moda de la distribución normal son iguales a la media aritmética de la distribución.

$Me=Mo=\mu$

El coeficiente de asimetría y el coeficiente de curtosis de la distribución normal son nulos.

$\begin{array}{c}A=0\\[2ex]C=0\end{array}$

La fórmula de la función de densidad de la distribución normal es la siguiente:

$\displaystyle P[X=x]=\frac1{\sigma\sqrt{2\pi}}\; e^{ - \frac{(x-\mu)^2}{2\sigma^2}}$

Asimismo, la fórmula de la función de probabilidad acumulada de la distribución normal es la siguiente:

$\displaystyle P[X\leq x]=\frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^x e^{-\frac{(x - \mu)^2}{2\sigma^2}}\, dx ,\quad x\in\mathbb{R}$

Una aplicación del teorema del límite central es que una distribución de Poisson se puede aproximar a una distribución normal cuando el valor de λ es suficientemente grande.

$\text{Poisson}(\lambda)\ \color{orange}\bm{\longrightarrow}\color{black} \ N\left(\lambda, \sqrt{\lambda}\right)$

Otra aplicación del teorema del límite central es que una distribución binomial se puede aproximar a una distribución normal para conjuntos de datos con un gran número de observaciones.

$\text{Bin}(n,p)\ \color{orange}\bm{\longrightarrow}\color{black} \ N\left(n\cdot p, \sqrt{n\cdot p \cdot (1-p)}\right)$

Distribución normal estándar

La distribución normal estándar, también llamada distribución normal unitaria, es el caso más simple de una distribución normal. En concreto, la distribución normal estándar es una distribución normal con valores de media y desviación estándar iguales a 0 y 1 respectivamente.

$\displaystyle N(0,1) \ \color{orange}\bm{\longrightarrow}\color{black}\begin{cases} \mu=0\\[2ex]\sigma=1\end{cases}$

Cabe destacar que cualquier distribución normal se puede transformar en una distribución normal estándar aplicando un proceso llamado tipificación que consiste en restar a cada uno de los valores su media aritmética y después dividir por su desviación típica.

Además, la distribución normal estándar se usa para determinar cualquier probabilidad de cualquier distribución normal mediante su tabla de probabilidades. De manera que para hallar una probabilidad de una distribución normal primero se tipifica la variable para convertirla en una distribución normal estándar y, posteriormente, se mira en la tabla cuál es el valor de la probabilidad correspondiente. Para saber más al respecto, haz clic en el siguiente enlace:

➤ Ver: Distribución normal estándar

La distribución normal y la regla empírica

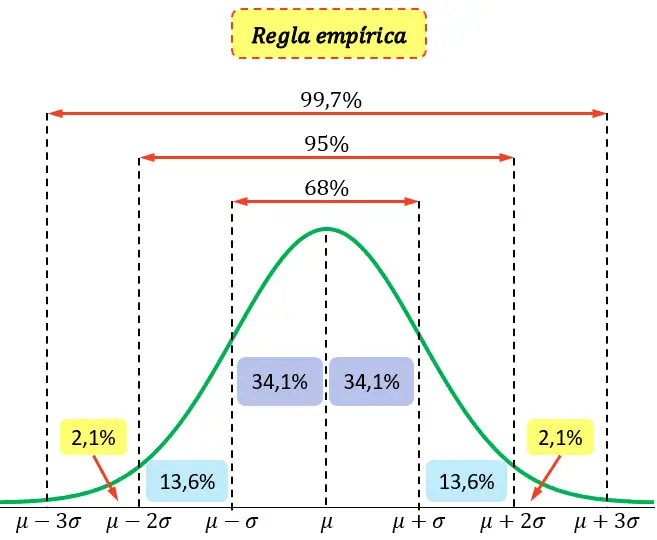
En estadística, la regla empírica, también llamada regla 68-95-99,7, es una regla que define el porcentaje de valores de una distribución normal que se encuentran a tres desviaciones estándar de la media.

En concreto, la regla empírica establece lo siguiente:

El 68% de los valores de una distribución normal se encuentran a una desviación estándar de la media.
El 95% de los valores de una distribución normal se encuentran a dos desviaciones estándar de la media.
El 99,7% de los valores de una distribución normal se encuentran a tres desviaciones estándar de la media.