En este artículo se explica qué es la distribución muestral de la diferencia de proporciones y para qué sirve en estadística. También se muestra la fórmula de la distribución muestral de la diferencia de proporciones y un ejercicio resuelto paso a paso.
Índice
¿Qué es la distribución muestral de la diferencia de proporciones?
La distribución muestral de la diferencia de proporciones es la distribución que resulta de calcular las diferencias entre las proporciones muestrales de todas las muestras posibles de dos poblaciones diferentes.
Es decir, el proceso para obtener la distribución muestral de la diferencia de proporciones consiste en, primero, extraer todas las muestras posibles de dos poblaciones diferentes, en segundo lugar, se determina la proporción de cada muestra extraída y, por último, se calcula la diferencia entre todas las proporciones de las dos poblaciones. De manera que el conjunto de resultados obtenidos después de hacer estas operaciones forman la distribución muestral de la diferencia de proporciones.
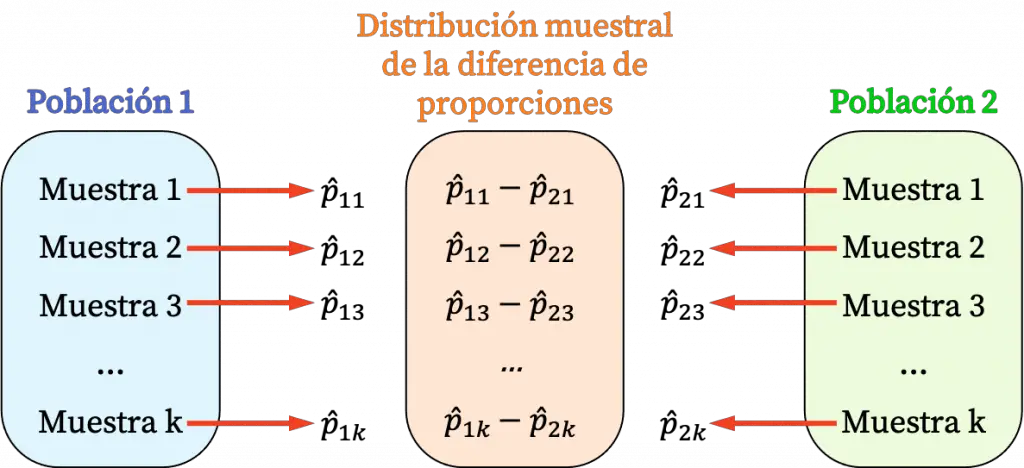
En estadística, la distribución muestral de la diferencia de proporciones sirve para calcular la probabilidad de que la diferencia entre las proporciones muestrales de dos muestras seleccionadas aleatoriamente se acerque a la diferencia de las proporciones poblacionales.
Fórmula de la distribución muestral de la diferencia de proporciones
Las muestras que se seleccionan para la distribución muestral de la diferencia de proporciones están definidas por distribuciones binomiales, ya que a efectos prácticos una proporción es una relación de los casos de éxito respecto al número total de observaciones.
No obstante, debido al teorema del límite central, las distribuciones binomiales se pueden aproximar a distribuciones de probabilidad normales. En consecuencia, la distribución muestral de la diferencia de proporciones se puede aproximar a una distribución normal con las siguientes características:
![\begin{array}{c}\displaystyle\mu_{\widehat{p_1}-\widehat{p_2}}=p_1-p_2 \qquad \sigma_{\widehat{p_1}-\widehat{p_2}}=\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\\[6ex]\displaystyle N_{p}\left(p_1-p_2, \sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\right) \end{array}](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-63f7c1b0409c12beae3015490187e9f1_l3.svg "Rendered by QuickLaTeX.com")
Nota: la distribución muestral de la diferencia de proporciones solo se puede aproximar a una distribución normal si 
, 
, 
, 
, 
y 
.
Por lo tanto, como se puede aproximar la distribución muestral de la diferencia de proporciones a una distribución normal, la fórmula para calcular el estadístico de la distribución muestral de la diferencia de proporciones es la siguiente:
Donde:
es la proporción de la muestra i.- es la proporción de la población i.
- es la probabilidad de fracaso de la población i, .
- es el tamaño de la muestra i.
- es una variable definida por la distribución normal estándar N(0,1).
es la proporción de la muestra i.
es la proporción de la población i.
es la probabilidad de fracaso de la población i, 
.
es el tamaño de la muestra i.
es una variable definida por la distribución normal estándar N(0,1).Esta fórmula es parecida a la fórmula de la prueba de hipótesis para la diferencia de proporciones.
Ejemplo resuelto de la distribución muestral de la diferencia de proporciones
Después de ver la definición de la distribución muestral de la diferencia de proporciones y cuál es su fórmula, a continuación puedes ver un ejemplo resuelto paso a paso para acabar de entender el concepto.
- Se quiere analizar la precisión de dos plantas de producción, una planta produce de manera que tan solo el 5% de las piezas producidas tienen defectos, mientras que el porcentaje de piezas defectuosas de otra planta es del 8%. Si tomamos una muestra de 200 piezas de la primera planta y otra muestra de 280 piezas de la segunda planta, ¿cuál es la probabilidad de que el porcentaje de defectos de la primera planta de producción sea mayor que el porcentaje de defectos de la segunda planta de producción?
Para acabar de conocer todos los datos del problema, primero calcularemos las proporción de piezas bien producidas de cada planta:
![\begin{array}{c}q_1=1-p_1=1-0,05=0,95\\[2ex]q_2=1-p_2=1-0,08=0,92\end{array}](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-c72bf6fc5b5f6dd26bf3a2d79aaa9143_l3.svg "Rendered by QuickLaTeX.com")
Si la proporción de defectos de la primera planta fuera más grande que la proporción de defectos de la segunda planta, significa que se cumpliría la siguiente ecuación:
Así pues, para determinar la probabilidad de la distribución muestral de la diferencia de proporciones tenemos que aplicar la fórmula explicada en el apartado de arriba:
De modo que la probabilidad de que la proporción de defectos de la primera planta sea mayor que la proporción de defectos de la segunda planta es equivalente a la probabilidad de que la variable Z sea mayor que 1,34:
![P[(\widehat{p_1}-\widehat{p_2})>0]=P[Z>1,34]](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-6daa240f3c985db4bd64b5246df3a6a7_l3.svg "Rendered by QuickLaTeX.com")
Por último, solo nos que buscar la probabilidad correspondiente en la tabla de la distribución normal y ya habremos resuelto el problema:
![P[(\widehat{p_1}-\widehat{p_2})>0]=P[Z>1,34]=0,0901](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-f5a1d35e69fe946ed56af45399cfbf0e_l3.svg "Rendered by QuickLaTeX.com")
En definitiva, la probabilidad de que la proporción de defectos de la primera planta sea mayor que la proporción de defectos de la segunda planta es del 9,01%.
