Diagrama de caja y bigotes (boxplot)

En este artículo se explica qué es un diagrama de caja y bigotes, también conocido como boxplot (o box plot). Encontrarás cómo se hacen este tipo de diagramas estadísticos y un ejercicio resuelto de un diagrama de caja y bigotes junto con su interpretación.

¿Qué es un diagrama de caja y bigotes?

El diagrama de caja y bigotes, también llamado diagrama de caja o boxplot, es un gráfico que representa un conjunto de datos estadísticos de manera visual utilizando los cuartiles.

La principal característica del diagrama de caja y bigotes es que permite visualizar rápidamente la dispersión de una serie de datos, ya que indica los cuartiles, la mediana, los valores extremos y los valores atípicos de los datos.

Así pues, este tipo de diagrama está formado por un caja rectangular y unas líneas (o bigotes) de los cuales destacan los siguientes valores:

• Los límites de la caja indican el primer y el tercer cuartil (Q₁ y Q₃). Y la línea vertical dentro de la caja es la mediana (equivalente al segundo cuartil Q₂).
• Los límites de los bigotes (o brazos) son los valores extremos, es decir, el valor mínimo y el valor máximo de la serie de datos.
• Los puntos fuera de los bigotes son los valores atípicos (outliers), o dicho con otras palabras, datos que probablemente se han medido mal y por tanto no deberían tenerse en cuenta en el estudio estadístico.

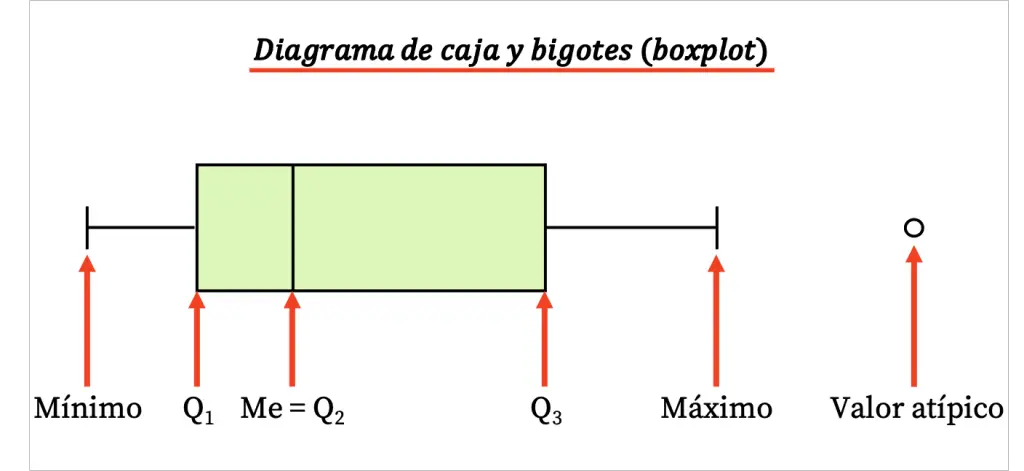
Fíjate que la diferencia entre el tercer y el primer cuartil es el rango intercuartílico (o rango intercuartil), otra medida de dispersión estadística.

Los diagramas de cajas y bigotes son muy útiles para comparar variables numéricas. Sin embargo, no es adecuado para representar variables categóricas.

Cómo hacer un diagrama de caja y bigotes

Para hacer un diagrama de caja y bigotes (o boxplot) a partir de una serie de datos, se deben hacer los siguientes pasos:

1. Ordenar los datos de la muestra estadística.
2. Calcular los cuartiles (Q₁, Q₂ y Q₃) y representarlos como la caja del diagrama. El primer y el tercer cuartil corresponden a los límites de la caja, y para representar la mediana (el segundo cuartil) se debe dibujar una línea dentro de la caja donde se encuentre su valor.
3. Calcular el rango intercuartílico, que es igual al tercer cuartil menos el primer cuartil.

   

4. Calcular los valores admisibles LI y LS, cuyas fórmulas son:

   

   

5. Identificar los valores atípicos de la muestra, que son aquellos valores menores que LI o mayores que LS. Representar dichos valores fuera del alcance de los bigotes con puntos.
6. Identificar y representar los valores extremos, que és el valor más pequeño y el valor más grande dentro del intervalo formado por LI y LS. Estos valores son el final de los dos bigotes del diagrama.

Ejemplo de diagrama de caja y bigotes

Vista la definición y la teoría del diagrama de caja y bigotes (o boxplot), a continuación tienes un ejemplo resuelto para entender mejor el concepto y ver cómo se hace este tipo de diagrama estadístico.

• Realiza el diagrama de caja y bigotes (o boxplot) del siguiente conjunto de datos estadísticos.

En este caso los datos ya están ordenados de menor a mayor, por lo que no hace falta hacer ninguna modificación. De lo contrario, primero tendríamos que ordenar los datos de la muestra.

En segundo lugar, sacamos los cuartiles de la muestra:

Una vez hemos calculado los tres cuartiles, hallamos el rango intercuartílico restando el cuartil 3 menos el cuartil 1:

Ahora calculamos los límites LI y LS, que son los valores a partir de los cuales se considera que un dato es atípico. Para ello, debemos utilizar las siguientes fórmulas:

De modo que en este caso tenemos dos valores atípicos, porque 3,02 es menor que 3,16 y 5,71 es mayor que 5,56.

Por último, faltan por identificar los valores extremos, que son el mínimo y el máximo de todos los datos que están dentro del intervalo [LI,LS]. Por lo tanto, en nuestro ejemplo el valor mínimo es 3,70 y el valor máximo es 4,81.

Así pues, una vez ya hemos identificado todos los valores del diagrama de caja y bigotes, solo nos queda hacer la representación gráfica:

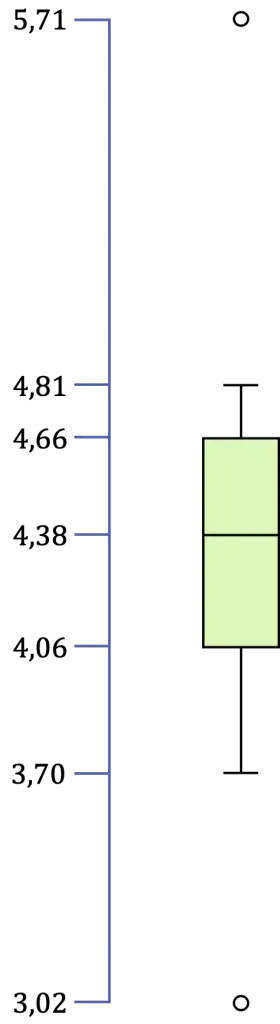
Para qué sirve un diagrama de caja y bigotes

Para terminar, vamos a ver para qué sirve y cómo interpretar el diagrama de caja y bigotes (o boxplot).

Evidentemente, el diagrama de caja y bigotes es muy útil para saber los cuartiles, el rango intercuartil, la mediana, los valores extremos y los valores atípicos de una serie de datos de manera rápida, ya que se pueden identificar todas estas medidas estadísticas a simple vista.

Además, el diagrama de caja y bigotes sirve para analizar la simetría de la muestra estadística, pues representa todo el conjunto de datos de manera visual. Si la mediana no está en el centro de la caja, significa que la muestra no es simétrica.

Asimismo, los boxplots se utilizan mucho en la bolsa para representar la variación del precio de una acción durante un periodo de tiempo, ya que permite ver el valor máximo, el valor mínimo y los valores intermedios en poco tiempo y así tomar decisiones más rápidas.