En este post se explica qué es la distribución uniforme continua y para qué sirve. También encontrarás la gráfica de la distribución uniforme continua y las propiedades de este tipo de distribución.
Índice
¿Qué es la distribución uniforme continua?
La distribución uniforme continua es un tipo de distribución de probabilidad en la cual todos los valores tienen la misma probabilidad de ocurrencia. Es decir, la distribución uniforme continua es una distribución en la que la probabilidad se distribuye uniformemente a lo largo de un intervalo.
La distribución uniforme continua se utiliza para describir variables continuas que tienen una probabilidad constante. Asimismo, la distribución uniforme continua se usa para definir procesos aleatorios, ya que si todos los resultados tienen la misma probabilidad significa que existe aleatoriedad en el resultado.
La distribución uniforme continua tiene dos parámetros característicos, a y b, que definen el intervalo de equiprobabilidad. Así pues, el símbolo de la distribución uniforme continua es U(a,b), donde a y b son los valores característicos de la distribución.
Por ejemplo, si el resultado de un experimento aleatorio puede tomar cualquier valor entre 5 y 9 y todos los posibles resultados tienen la misma probabilidad de ocurrir, el experimento se puede simular con una distribución uniforme continua U(5,9).
La distribución uniforme continua también se llama distribución rectangular.
Fórmula de la distribución uniforme continua
La función de densidad que define la probabilidad de la distribución uniforme es uno partido por la diferencia entre b y a. Por lo tanto, la fórmula de la distribución uniforme continua es la siguiente:
![\begin{array}{c}X\sim U(a,b)\\[2ex]f(x)=\cfrac{1}{b-a}\\[4ex]x\in [a,b]\end{array}](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-6fcae133b3e510f05c22c0890dcd739b_l3.svg "Rendered by QuickLaTeX.com")
Por otro lado, la función de probabilidad acumulada de la distribución uniforme continua se define mediante la siguiente expresión:
![\displaystyle F(x)=\left\{\begin{array}{ll}0&\text{si }x<a\\ \cfrac{x-a}{b-a}&\text{si }a\leq x<b\\[2ex]1&\text{si }x\geq b\end{array}\right.](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-faa8f23b6ed4e6284c640227adc8bef3_l3.svg "Rendered by QuickLaTeX.com")
Gráfica de la distribución uniforme continua
Como en una distribución uniforme continua la probabilidad es constante, su representación gráfica es simplemente una función con un valor constante definida en el mismo intervalo que la distribución uniforme.
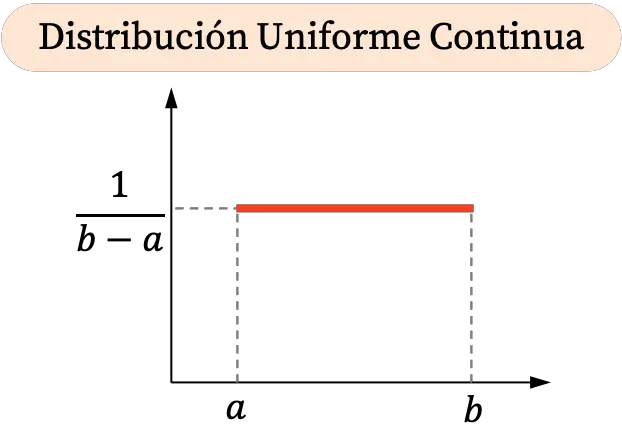
Por otro lado, la gráfica de la probabilidad acumulada de la distribución uniforme continua es la siguiente:
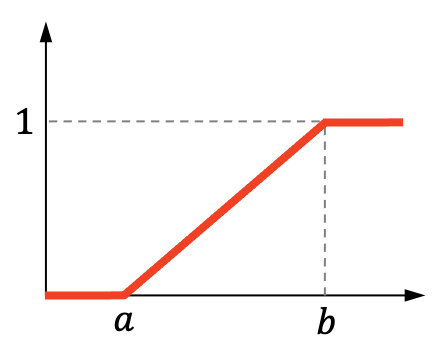
Características de la distribución uniforme continua
La distribución uniforme continua tiene las siguientes características:
- La distribución uniforme continua queda definida por dos parámetros reales, a y b, que establecen los límites dentro de los cuales la probabilidad es constante.
- La distribución uniforme continua solo puede tomar valores que se encuentren dentro del intervalo formado por a y b, ambos incluidos.
![x\in [a,b]](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-2067b31aff8c9be7d21cbcb549a54332_l3.svg "Rendered by QuickLaTeX.com")
- La media de una distribución uniforme continua es igual a la suma de sus dos parámetros característicos partido por dos.
![E[X]=\cfrac{a+b}{2}](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-7c230ec8a572104bf91fa425fa603df3_l3.svg "Rendered by QuickLaTeX.com")
- La varianza de una distribución uniforme continua es equivalente al cuadrado de la diferencia entre b y a dividido por doce.
- La mediana de una distribución uniforme continua coincide con su media, por lo que se calcula utilizando la misma fórmula:
- La distribución uniforme continua es simétrica, por lo tanto, el coeficiente de asimetría de este tipo de distribución es nulo.
- La curtosis de una distribución uniforme continua no depende de sus parámetros, siempre vale -6 partido por 5.
- La distribución uniforme estándar es aquella distribución uniforme continua cuyos parámetros a y b valen 0 y 1 respectivamente.
Distribución uniforme continua y distribución uniforme discreta
Por último, veremos cuál es la diferencia entre la distribución uniforme continua y la distribución uniforme discreta, ya que son dos distribuciones de probabilidad que pueden confundirse pero representan conceptos totalmente distintos.
La principal diferencia entre una distribución uniforme continua y una distribución uniforme discreta son los valores que pueden tomar. Una distribución uniforme continua está definida en un espacio muestral continuo, en cambio, una distribución uniforme discreta está definida en un espacio muestral discreto.
Por lo tanto, la distribución uniforme discreta solo puede tomar algunos valores dentro de un intervalo, generalmente números enteros, mientras que una distribución uniforme continua puede tomar cualquier valor dentro de un intervalo, incluyendo números decimales.