▷ Distribución F de Snedecor

En este post se explica qué es la distribución F de Snedecor y para qué sirve. Además, podrás ver la gráfica de la distribución F de Snedecor y cuáles son sus propiedades estadísticas.

Índice

¿Qué es la distribución F de Snedecor?

La distribución F de Snedecor, también llamada distribución F de Fisher-Snedecor o simplemente distribución F, es una distribución de probabilidad continua que se usa en la inferencia estadística, especialmente en el análisis de la varianza.

Una de las propiedades de la distribución F de Snedecor es que queda definida por el valor de dos parámetros reales, m y n, que indican sus grados de libertad. Así pues, el símbolo de la distribución F de Snedecor es F_m,n, donde m y n son los parámetros que definen la distribución.

$F_{m,n}\qquad m,n>0$

Matemáticamente, la distribución F de Snedecor es igual al cociente entre una distribución chi-cuadrado y sus grados de libertad partido por el cociente entre otra distribución chi-cuadrado y sus grados de libertad. De modo que la fórmula que define la distribución F de Snedecor es la siguiente:

$\left.\begin{array}{c} X\sim \chi_m^2\\[2ex] Y\sim \chi_n^2\end{array}\right\}\color{orange}\bm{\longrightarrow}\color{black}\ F_{m,n}= \cfrac{X/m}{Y/n}$

➤ Ver: ¿Qué es la distribución chi-cuadrado?

La distribución F de Fisher-Snedecor recibe este nombre en honor al estadístico inglés Ronald Fisher y al estadístico estadounidense George Snedecor.

En estadística, la distribución F de Fisher-Snedecor tiene diferentes aplicaciones. Por ejemplo, la distribución F de Fisher-Snedecor se usa para comparar diferentes modelos de regresión lineal, asimismo, esta distribución de probabilidad se utiliza en el análisis de la varianza (ANOVA).

Gráfica de la distribución F de Snedecor

Una vez vista la definición de la distribución F de Snedecor, a continuación se muestra la gráfica de su función de densidad y la gráfica de su probabilidad acumulada.

En el gráfico de abajo puedes ver representados varios ejemplos de distribuciones F de Snedecor con diferentes grados de libertad.

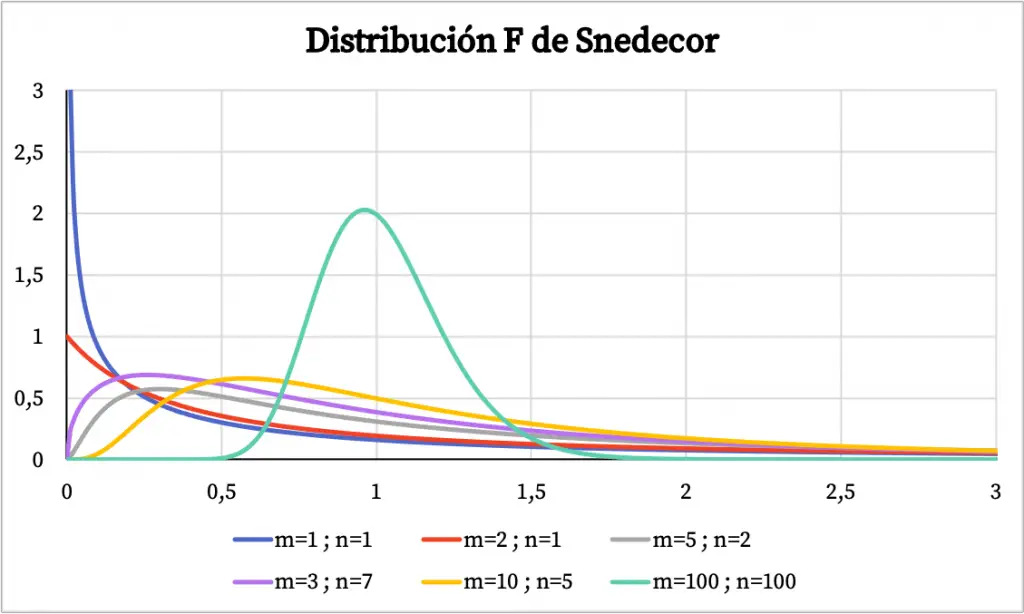
gráfica de la distribución F de Snedecor

Por otro lado, en el gráfico de abajo puedes ver cómo varia la gráfica de la función de probabilidad acumulada de la distribución F de Snedecor según sus valores característicos.

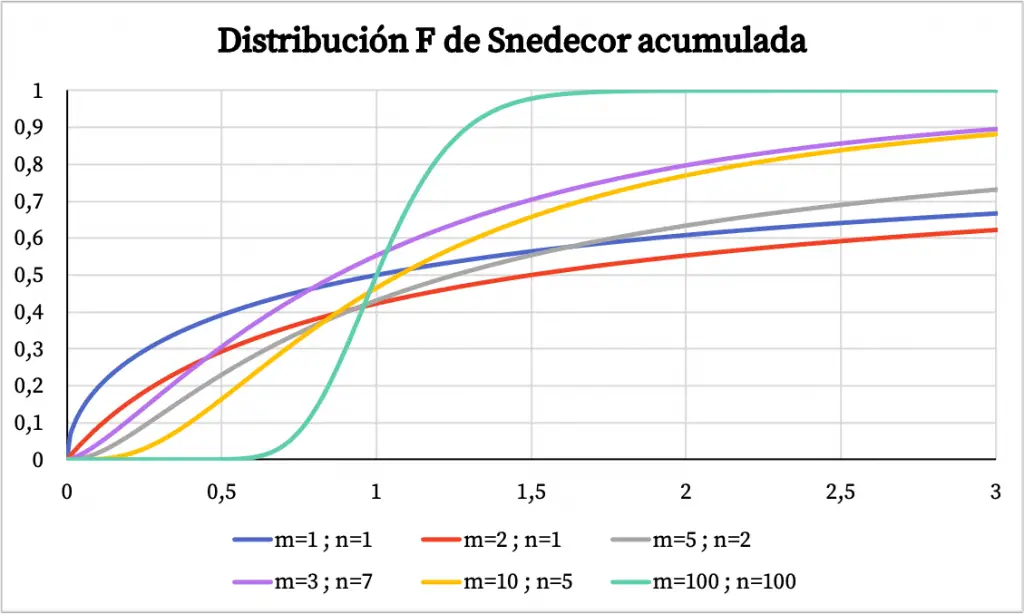
Características de la distribución F de Snedecor

Por último, en este apartado se muestran las características más importantes de la distribución F de Snedecor.

Los grados de libertad de la distribución F de Snedecor, m y n, son dos parámetros que definen la forma de la distribución. Estos valores característicos de la distribución F de Snedecor son números enteros y positivos.

$\begin{array}{c}m,n \in \mathbb{Z}\\[2ex] m,n>0\end{array}$

El dominio de la distribución F de Snedecor son todos los números reales mayores o igual que cero.

$x\in [0,+\infty)$

Para valores de n más grandes que 2, la media de la distribución F de Snedecor es igual a n partido por la resta de n menos 2.

$\begin{array}{c}X\sim F_{m,n}\\[2ex] E[X]=\cfrac{n}{n-2} \qquad \text{para }n>2\end{array}$

Cuando el parámetro n es mayor que 2, se puede calcular la varianza de la distribución F de Snedecor aplicando la siguiente fórmula:

$\begin{array}{c}X\sim F_{m,n}\\[2ex] Var(X)=\cfrac{2n^2\cdot (m+n-2)}{m\cdot (n-2)^2\cdot (n-4)} \qquad \text{para }n>4\end{array}$

Si el parámetro m es mayor que 2, la moda de la distribución F de Snedecor se puede calcular con la siguiente expresión:

$Mo=\cfrac{m-2}{m}\cdot \cfrac{n}{n+2}\qquad \text{para }m>2$

La fórmula de la función de densidad de la distribución F de Snedecor es la siguiente:

$\displaystyle P[X=x]=\frac{\Gamma\left(\frac{m+n}{2}\right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\left(\frac{m}{n}\right)^{\frac{m}{2}}\cdot\frac{x^{\frac{m-2}{2}}}{\left(1+\frac{mx}{n}\right)^{\frac{m+n}{2}}}$

Si una variable sigue una distribución F de Snedecor con grados de libertad m y n, entonces la inversa de dicha variable sigue una distribución F de Snedecor con los mismos grados de libertad pero cambiando el orden de sus valores.

$X\sim F_{m,n} \ \color{orange}\bm{\longrightarrow}\color{\black} \ X^{-1}\sim F_{n,m}$