Intervalo de confianza

En este artículo se explica qué es un intervalo de confianza en estadística y para qué sirve. Asimismo, encontrarás los factores que influyen en los intervalos de confianza y cómo se calcula un intervalo de confianza.

¿Qué es un intervalo de confianza?

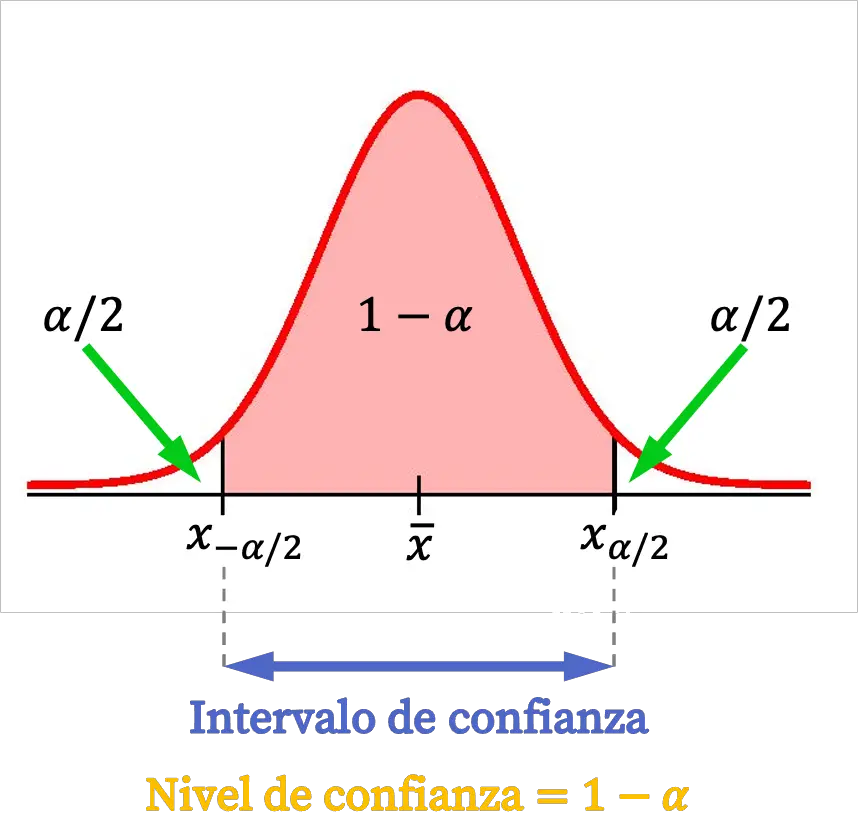
En estadística, el intervalo de confianza es un intervalo que da una aproximación de los valores entre los cuales se encuentra el valor de un parámetro poblacional con un determinado nivel de confianza. Los intervalos de confianza más habituales tienen un nivel de confianza del 95% o del 99%.

Por ejemplo, si el intervalo de confianza para la media de una población con un nivel de confianza del 95% es (3,7), significa que la media de la población estudiada estará entre 3 y 7 con una probabilidad del 95%.

Por lo tanto, el intervalo de confianza sirve para estimar dos valores entre los cuales se encuentra un parámetro de la población. Generalmente, los valores de los parámetros poblaciones se desconocen, así que se calcula un intervalo de confianza a partir de los datos de una muestra para tener una estimación de los parámetros poblacionales.

Factores que influyen en el intervalo de confianza

Una vez hemos visto la definición de intervalo de confianza, vamos a ver cuáles son los factores de los que dependen los intervalos de confianza para entender mejor el concepto.

  • Tamaño muestral: el número de observaciones estudiadas influye en la precisión del intervalo de confianza, ya que cuantos más datos se tengan mejor se puede estimar un valor. En general, cuanto más grande sea el tamaño de la muestra, menor será la amplitud del intervalo de confianza.
  • Margen de error: cuanto mayor sea el error permitido, más grande será el intervalo de confianza y, por tanto, más probable es de que el valor real del parámetro esté dentro del intervalo de confianza. No obstante, el margen de error disminuye la precisión del intervalo de confianza.
  • Nivel de confianza: es la probabilidad de que la estimación del parámetro estadístico de la población se encuentre dentro del intervalo de confianza. Normalmente, el nivel de confianza de un intervalo se indica por 1-α y se expresa en forma de porcentaje. Un nivel de confianza alto aumenta la probabilidad de que el valor real se encuentre entre los límites del intervalo, pero también aumenta la amplitud del intervalo.
  • El parámetro estimado: el intervalo de confianza depende del parámetro que se quiera aproximar. De hecho, la fórmula que se debe utilizar para calcular el intervalo de confianza depende del parámetro aproximado.

Cómo calcular el intervalo de confianza

A continuación se muestra la fórmula que se debe aplicar para calcular cada tipo de intervalo de confianza, ya que según si se quiere determinar el intervalo de confianza para la media, la varianza o la proporción, la fórmula que se debe emplear es diferente.

Intervalo de confianza para la media

Partiendo de que el proceso de tipificación de una variable se hace de la siguiente manera:

Z=\cfrac{X-\mu}{\displaystyle\frac{\sigma}{\sqrt{n}}} \sim N(0,1)

El intervalo de confianza para la media se calcula sumando y restando a la media muestral el valor de Zα/2 multiplicado por la desviación típica (σ) y dividido por la raíz cuadrada del tamaño de la muestra (n). Por lo tanto, la fórmula para calcular el intervalo de confianza para la media es la siguiente:

\displaystyle \left(\overline{x}-z_{\alpha/2}\cdot \frac{\sigma}{\sqrt{n}} \ , \ \overline{x}+z_{\alpha/2}\cdot \frac{\sigma}{\sqrt{n}} \right)

Para tamaños muestrales grandes y un nivel de confianza del 95% el valor crítico es Zα/2=1,96 y para un nivel de confianza del 99% el valor crítico es Zα/2=2,576.

La fórmula anterior se utiliza cuando la varianza de la población es conocida. No obstante, si la varianza de la población es desconocida, que es el caso más frecuente, el intervalo de confianza para la media se calcula con la siguiente fórmula:

\displaystyle \left(\overline{x}-t_{\alpha/2}\cdot \frac{s}{\sqrt{n}} \ , \ \overline{x}+t_{\alpha/2}\cdot \frac{s}{\sqrt{n}} \right)

Donde:

  • \overline{x}es la media de la muestra.
  • t_{\alpha/2}es el valor de la distribución t de Student de n-1 grados de libertad con una probabilidad de α/2.
  • ses la desviación típica de la muestra.
  • nes el tamaño de la muestra.
intervalo de confianza

Intervalo de confianza para la varianza

Para calcular el intervalo de confianza para la varianza de una población se utiliza la distribución chi-cuadrado. En concreto, la fórmula para calcular el intervalo de confianza para la varianza es la siguiente:

\displaystyle \left( (n-1)\frac{s^2}{\chi_{n-1;\alpha/2}} \ , \ (n-1)\frac{s^2}{\chi_{n-1;1-\alpha/2}}\right)

Donde:

  • nes el tamaño de la muestra.
  • ses la desviación típica de la muestra.
  • \chi_{n-1;\alpha/2}es el valor de la distribución chi-cuadrado con n-1 grados de libertad para una probabilidad inferior a α/2.
  • \chi_{n-1;1-\alpha/2}es el valor de la distribución chi-cuadrado con n-1 grados de libertad para una probabilidad superior a 1-α/2.

Intervalo de confianza para la proporción

El intervalo de confianza para la proporción se calcula sumando y restando a la proporción de la muestra el valor de Zα/2 multiplicado por la raíz cuadrada de la proporción muestral (p) multiplicado por 1-p y divido por el tamaño de la muestra (n). Por lo tanto, la fórmula para calcular el intervalo de confianza para la proporción es la siguiente:

\displaystyle \left(p-Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\ , \ p+Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\right)

Donde:

  • pes la proporción de la muestra.
  • nes el tamaño de la muestra.
  • Z_{\alpha/2}es el cuantil de la distribución normal estándar correspondiente a una probabilidad de α/2. Para tamaños muestrales grandes y un nivel de confianza del 95% se suele aproximar a 1,96 y para una confianza del 99% se suele aproximar a 2,576.

4 comentarios en “Intervalo de confianza”

  1. Irma Nieto

    ¡Excelente trabajo!, muy resumido y claro, su página es una consulta confiable para mis clases. ¡Muchas gracias por su esfuerzo!

    Responder
    1. Probabilidad y Estadística

      ¡Muchísimas gracias Irma! ¡Me alegro de que te guste la página! Cualquier duda sobre las clases puedes preguntarnos e intentaremos ayudarte.

  2. Laura Medina

    Super completas todas las entradas y la información proporcionada, es muy útil y claras. Muchas gracias por tan buen trabajo y esfuerzo que contribuye al conocimiento y la agilidad para todos nosotros.

    Responder
    1. Probabilidad y Estadística

      ¡Muchísimas gracias Laura! ¡Me alegro de que te resulte útil la página web!

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Scroll al inicio