Diagrama de dispersión

En este artículo se explica qué son los diagramas de dispersión. De modo que encontrarás para qué sirve un diagrama de dispersión, cómo se hace un diagrama de dispersión, cómo se interpreta y ejemplos de diagramas de dispersión.

¿Qué es un diagrama de dispersión?

El diagrama de dispersión, o gráfico de dispersión, es un tipo de diagrama estadístico en el que se representa gráficamente un conjunto de datos de dos variables en dos ejes de coordenadas cartesianas.

Por lo tanto, los diagramas de dispersión sirven para analizar la relación entre dos variables estadísticas.

Los diagramas de dispersión reciben varios nombres diferentes, tales como diagrama de correlación o nube de puntos.

Cabe destacar que el diagrama de dispersión se considera como una de las herramientas básicas de control de calidad, junto con el diagrama de Pareto, el diagrama de causa-efecto, el diagrama de flujo, etc.

Cómo hacer un diagrama de dispersión

Para hacer un diagrama de dispersión debes seguir los siguientes pasos:

1. Recolectar los datos estadísticos de la muestra que se quiere analizar. Ten en cuenta que para poder hacer un diagrama de dispersión deben haber como mínimo dos variables cuantitativas.
2. Representar los dos ejes del gráfico de dispersión.
3. Determinar las dos variables estadísticas que se representarán gráficamente.
4. Calibrar la escala de cada eje de la gráfica. Para ello, se recomienda encontrar primero el mínimo y el máximo de cada variable y, a partir de estos valores, graduar cada eje.
5. Representar cada pareja de datos en el diagrama de dispersión con un punto.
6. Analizar e interpretar el diagrama de dispersión obtenido.

Ejemplo de diagrama de dispersión

Después de ver la definición de diagrama de dispersión y la teoría sobre cómo se hace, en este apartado se representa un diagrama de este tipo a modo de ejemplo.

• En la siguiente tabla de frecuencia, se han recogido como datos las notas de matemáticas y estadística de una muestra de 20 alumnos. Representa el conjunto de datos en un diagrama de dispersión y analízalo.

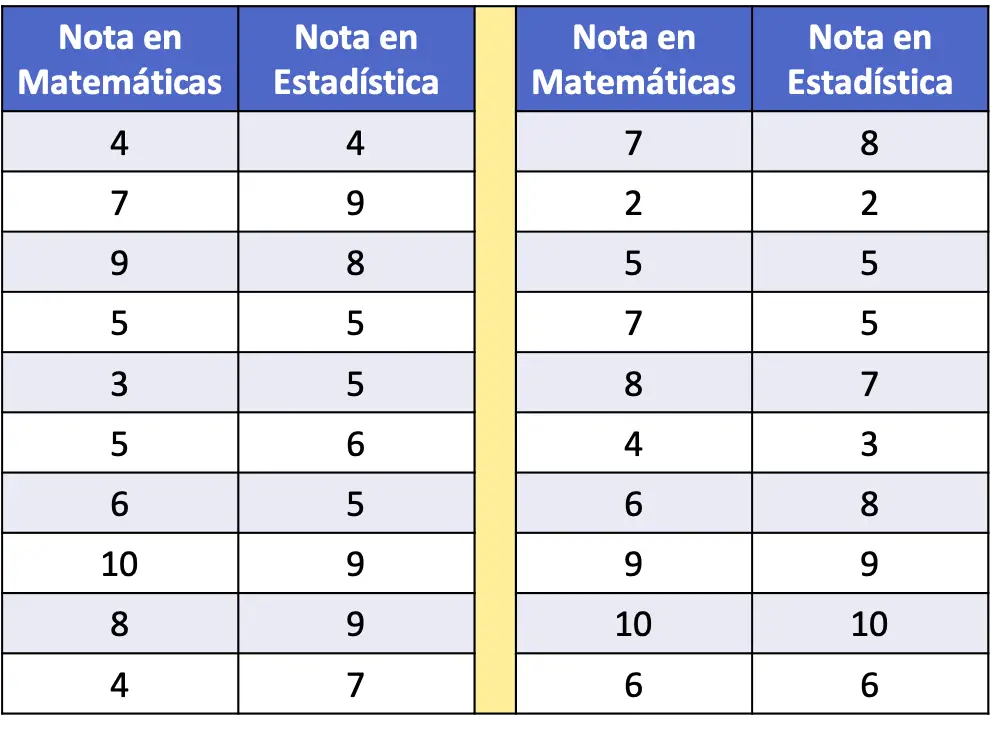
Para representar la serie de datos en un diagrama de dispersión simplemente debemos dibujar dos ejes, calibrarlos y representar un punto en la gráfica para cada pareja de datos. Recuerda que un punto en una gráfica se pone donde se cortan las rectas imaginarias correspondientes a cada uno de sus valores.

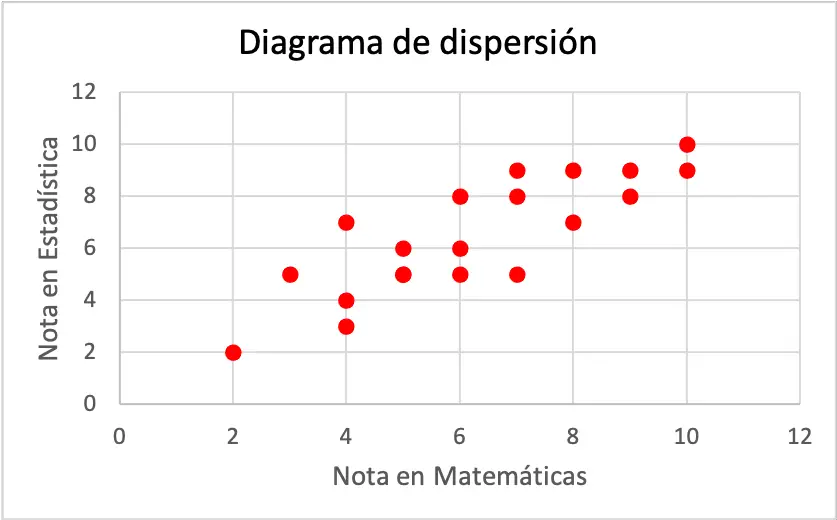
Cada eje del diagrama de dispersión representa una variable. En concreto, el eje horizontal pertenece a la nota conseguida en matemáticas y, por otro lado, el eje vertical corresponde a la nota obtenida en estadística.

Como puedes ver en el gráfico de dispersión, las dos variables tienen una correlación positiva, ya que una variable aumenta a medida que la otra variable también aumenta. Por lo tanto, se concluye que si un alumno consigue mejor nota en matemáticas es más probable que también saque mejor nota en estadística, y al revés.

Sin embargo, la conclusión anterior no significa que una variable sea la causa de la otra, ya que obtener una buena nota en matemáticas no te garantiza automáticamente conseguir una buena nota en estadística sin hacer nada, sino que se deben estudiar las dos asignaturas. En el siguiente apartado entraremos más en detalle en este concepto.

El diagrama de dispersión y la correlación

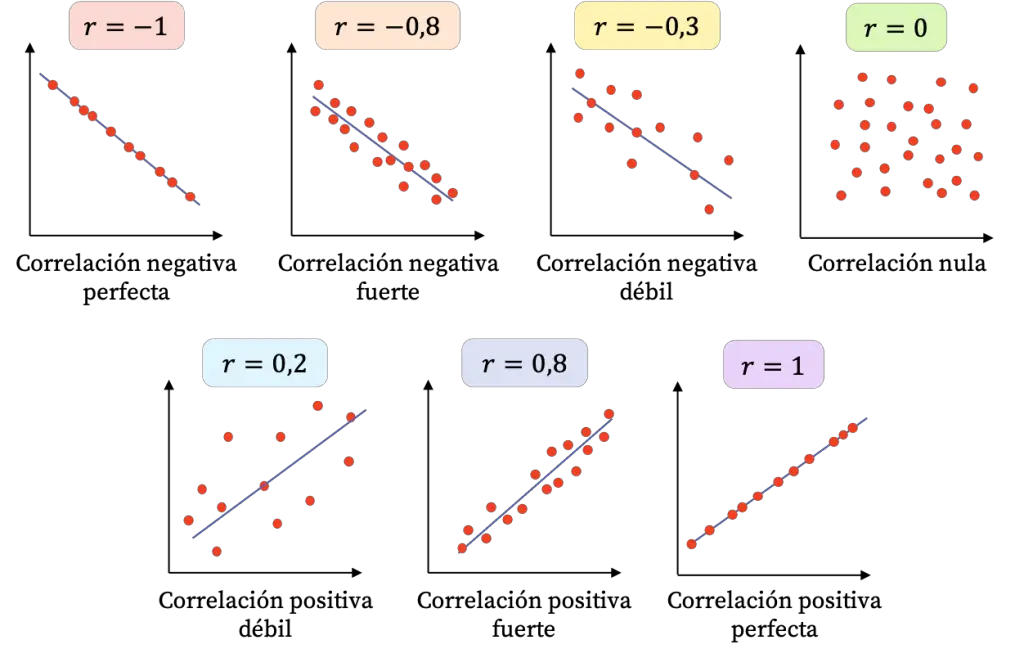
A partir de un diagrama de dispersión se puede identificar qué tipo de correlación tienen dos variables:

• Correlación directa (o correlación positiva): una variable aumenta cuando la otra también aumenta.
• Correlación inversa (o correlación negativa): cuando una variable aumenta la otra disminuye, y al revés, si una variable disminuye la otra aumenta.
• Correlación nula (sin correlación): no existe ninguna relación entre las dos variables.

Asimismo, independientemente de si la correlación entre las dos variables es directa o inversa, la correlación también se puede clasificar en función de cuanto de fuerte o débil es la relación entre ambas variables.

• Correlación fuerte: las dos variables están muy relacionadas. Los puntos están muy juntos entre sí en el diagrama de dispersión. En consecuencia, resulta más fácil identificar la relación entre las variables.
• Correlación débil: existe una relación entre las dos variables, pero resulta difícil de identificar. Los puntos están muy separados en el diagrama de dispersión.

Por otro lado, la correlación también se puede calcular numéricamente mediante una fórmula, así se puede saber matemáticamente cuánto de relacionadas están dos variables diferentes. Para ver cómo se hace, haz clic en el siguiente enlace:

Ten presente que aunque haya correlación entre dos variables esto no significa que exista causalidad entre ellas, es decir, la correlación entre dos variables no significa que el cambio en una variable sea la causa del cambio en la otra variable.

Así pues, siguiendo el ejemplo del gráfico de dispersión del apartado anterior, aunque existe una correlación positiva entre la nota de matemáticas y la de estadística, conseguir una buena nota en matemáticas no implica sacar una buena nota en estadística, pues si solo estudias matemáticas seguramente suspenderás estadística. Por lo tanto, las dos variables están relacionadas pero no son causa y efecto.

Para saber más al respecto, puedes seguir con el siguiente post:

Ventajas y desventajas del diagrama de dispersión

Debido a las características del diagrama de dispersión, este tipo de gráficos estadísticos tienen sus ventajas y sus desventajas.

Ventajas:

• Resulta bastante fácil representar una serie de datos en un diagrama de dispersión.
• El diagrama de dispersión permite analizar de manera visual la relación entre dos variables, lo que facilita extraer conclusiones.
• Los gráficos de dispersión también pueden utilizarse en un estudio estadístico exhaustivo como una exploración previa de los datos.

Desventajas:

• Este tipo de diagramas no son útiles para representar variables cualitativas.
• La interpretación de un diagrama de dispersión puede llevar a una conclusión errónea de causa-efecto entre dos variables.
• Los diagramas de dispersión no permiten analizar la relación entre más de dos variables.