▷ Distribución Exponencial

En este post se explica qué es la distribución exponencial en estadística y para qué sirve. Asimismo, encontrarás cuáles son las propiedades de la distribución exponencial junto con sus fórmulas, su gráfica y un ejercicio resuelto. Además, podrás calcular cualquier probabilidad con una calculadora online de la distribución exponencial.

Índice

¿Qué es la distribución exponencial?

La distribución exponencial es una distribución de probabilidad continua que sirve para modelizar el tiempo de espera para la ocurrencia de un fenómeno aleatorio.

En concreto, la distribución exponencial permite describir el tiempo de espera entre dos fenómenos que siguen una distribución de Poisson. Por lo tanto, la distribución exponencial está estrechamente relacionada con la distribución de Poisson.

➤ Ver: ¿Qué es la distribución de Poisson?

La distribución exponencial tiene un parámetro característico, que se representa con la letra griega λ e indica el número de veces que se espera que ocurra el evento estudiado durante un periodo de tiempo determinado.

$X\sim \text{Exp}(\lambda)$

Asimismo, la distribución exponencial también se usa para modelizar el tiempo que transcurre hasta que se produce un fallo. De modo que la distribución exponencial tiene varias aplicaciones en fiabilidad y en la teoría de la supervivencia.

Ejemplos de distribuciones exponenciales

Ahora que ya sabemos la definición de la distribución exponencial, vamos a ver varios ejemplos de este tipo de distribución para entender mejor el concepto.

Ejemplos de la distribución exponencial:

El tiempo transcurrido entre dos llamadas en un centro de atención de llamadas.
El tiempo que debe esperar una persona hasta que pasa un taxi libre por una calle concreta.
El tiempo de espera hasta que entra un nuevo cliente en una tienda.
El tiempo que transcurre entre la entrada de dos usuarios diferentes en una página web.
El tiempo que transcurre en un aeropuerto desde que despega un avión hasta que sale otro.

Fórmula de la distribución exponencial

La fórmula de la función de densidad que define el cálculo de una probabilidad de la distribución exponencial es igual a λ multiplicado por el número e elevado a menos λ por x.

Es decir, la fórmula para calcular una probabilidad de la distribución exponencial es la siguiente:

👉 Puedes usar la calculadora que hay más abajo para calcular la probabilidad de una variable que sigue la distribución exponencial.

Por otro lado, la fórmula para calcular una probabilidad acumulada de la distribución exponencial es la siguiente:

$P[X\leq x]=1-e^{-\lambda x}$

Gráfica de la distribución exponencial

En este apartado puedes ver la representación gráfica de la función de densidad y de la función de distribución de la distribución exponencial.

A continuación puedes ver cómo varia la gráfica de la función de densidad de la distribución exponencial según el valor del parámetro λ.

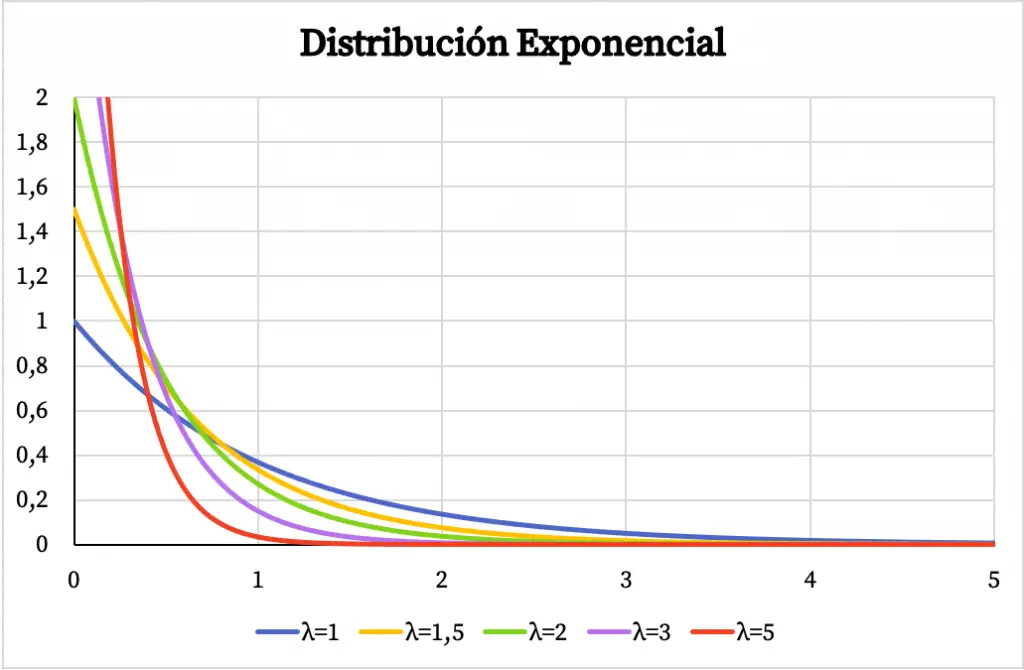
Asimismo, la función de probabilidad acumulada de la distribución exponencial también depende del valor del parámetro λ, tal y como puedes ver en el siguiente gráfico:

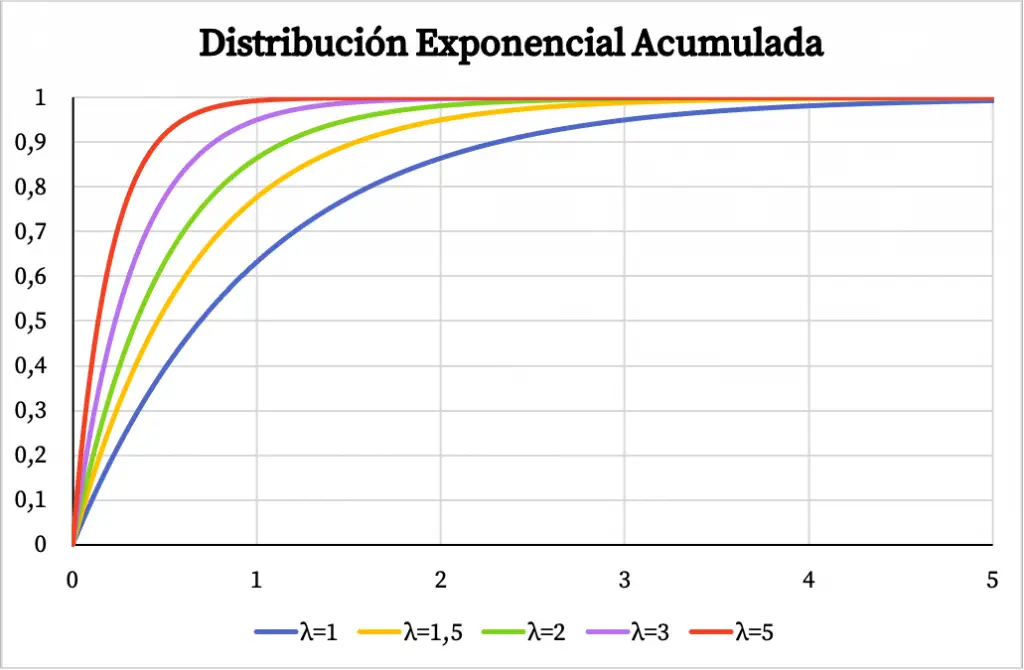
gráfica de probabilidad acumulada de la distribución exponencial

Ejercicio resuelto de la distribución exponencial

En una página web concreta entran una media de λ=1 usuarios/min. ¿Cuál es la probabilidad de que el tiempo que transcurre entre la entrada de dos usuarios sea de 3 minutos? ¿Y la probabilidad de que sea igual o menos de 2 minutos?

La distribución que define la variable aleatoria de este problema es una distribución exponencial, ya que estamos estudiando el tiempo que pasa desde que sucede un evento (la entrada de un usuario a la página web) hasta que vuelve a suceder ese mismo evento.

$X\sim \text{Exp}(1)$

Por lo tanto, para calcular la probabilidad de que el tiempo transcurrido entre la entrada de dos usuarios diferentes sea de tres minutos tenemos que aplicar la fórmula de la función densidad (vista más arriba):

$\begin{aligned}P[X=x]&=\lambda e^{-\lambda x}\\[2ex]P[X=3]&=1\cdot e^{-1\cdot 3}\\[2ex]P[X=3]&=0,05\end{aligned}$

Por otro lado, para determinar una probabilidad acumulada tenemos que utilizar la fórmula de la función de distribución de la distribución exponencial:

$\begin{aligned}P[X\leq x]&=1- e^{-\lambda x}\\[2ex]P[X\leq 2]&=1-e^{-1\cdot 2}\\[2ex]P[X\leq 2]&=0,86\end{aligned}$

Características de la distribución exponencial

La distribución exponencial cumple con las siguientes características:

La distribución exponencial tiene un parámetro característico, λ, que indica el número de veces que se espera que ocurra el fenómeno estudiado durante un periodo de tiempo determinado.

$X\sim \text{Exp}(\lambda)$

La distribución exponencial no puede tomar un valor negativo, por lo que el dominio de la distribución exponencial son todos los números reales mayores o igual que cero.

$x\in [0,+\infty)$

La media de la distribución exponencial es igual a uno partido por el parámetro característico λ.

$E[X]=\cfrac{1}{\lambda}$

La varianza de la distribución exponencial es el cuadrado de su media, por lo tanto, la varianza de la distribución exponencial es equivalente a uno partido por el coeficiente λ al cuadrado.

$Var(X)=\cfrac{1}{\lambda^2 }$

Independientemente del valor de λ, el coeficiente de asimetría de la distribución exponencial siempre es igual a 2.

$A=2$

Asimismo, el coeficiente de curtosis de cualquier distribución exponencial siempre es equivalente a 9.

$C=9$

La fórmula de la función de densidad de la distribución exponencial es la siguiente:

$P[X=x]=\lambda e^{-\lambda x}$

Mientras que la fórmula de la función de probabilidad acumulada de la distribución exponencial es la siguiente:

$P[X\leq x]=1-e^{-\lambda x}$

La distribución exponencial es una de las pocas distribuciones de probabilidad que tienen la propiedad de falta de memoria. Esta propiedad significa que la ocurrencia de un evento anterior no afecta a la probabilidad de que suceda ese evento en el futuro. Por ejemplo, en una distribución exponencial la probabilidad de que un nuevo usuario entre en una página web en menos de un minuto no depende de si justo acaba de entrar un usuario o si hace más de diez minutos que no entra ningún usuario.

$P[X>x+y|X>y]=P[X>x]$

Calculadora de la distribución exponencial

Introduce el valor del parámetro λ y el valor de x en la siguiente calculadora para calcular la probabilidad. Debes seleccionar la probabilidad que quieres calcular e introducir los números utilizando el punto como separador decimal, por ejemplo, 0.50.