Regla de la multiplicación

En este post se explica qué es la regla de la multiplicación, también llamada regla del producto, en la teoría de la probabilidad. Así pues, encontrarás cuál es la fórmula de la regla de multiplicación, ejemplos de cómo calcular una probabilidad utilizando la regla de la multiplicación y, además, varios ejercicios resueltos para practicar.

La regla de la multiplicación depende de si los eventos son independientes o dependientes, por lo que primero veremos cómo es la regla para eventos independientes y posteriormente para eventos dependientes.

Regla de la multiplicación para eventos independientes

Recuerda que los los eventos independientes son aquellos resultados de un experimento estadístico cuya probabilidad de ocurrencia no dependen entre sí. Es decir, dos eventos A y B son independientes si la probabilidad de que suceda el evento A no depende de que ocurra el evento B y viceversa.

Fórmula de la regla de la multiplicación para eventos independientes

Cuando dos eventos son independientes, la regla de la multiplicación dice que la probabilidad conjunta de que ocurran los dos eventos es igual al producto entre la probabilidad de ocurrencia de cada evento.

Por lo tanto, la fórmula de la regla de la multiplicación para eventos independientes es la siguiente:

P(A\cap B)=P(A)\cdot P(B)

Donde:

  • A y B son dos eventos independientes.
  • P(A\cap B) es la probabilidad conjunta de que ocurra el evento A y el evento B.
  • P(A) es la probabilidad de que ocurra el evento A.
  • P(B) es la probabilidad de que ocurra el evento B.

Ejemplo de la regla de la multiplicación para eventos independientes

  • Se procede a hacer el lanzamiento de una moneda tres veces seguidas. Calcula la probabilidad de obtener cara en los tres lanzamientos.

En este caso, los eventos de los cuales queremos calcular la probabilidad conjunta son independientes, ya que el resultado del lanzamiento de una moneda no depende del resultado obtenido en el lanzamiento anterior. Por lo tanto, para determinar la probabilidad conjunta de obtener tres veces consecutivas cara debemos utilizar la fórmula de la regla de la multiplicación para eventos independientes:

P(A\cap B)=P(A)\cdot P(B)

En el lanzamiento de una moneda solo hay dos posibles resultados, podemos obtener cara o cruz. Por lo tanto, la probabilidad de obtener cara o cruz al lanzar una moneda es:

P(\text{cara})=\cfrac{1}{2}=0,5

P(\text{cruz})=\cfrac{1}{2}=0,5

Así pues, para hallar la probabilidad de obtener cara en los tres lanzamientos de moneda tenemos que multiplicar tres veces la probabilidad de sacar cara por sí misma:

P(\text{cara}\cap \text{cara}\cap \text{cara})=0,5\cdot 0,5\cdot 0,5=0,125

En definitiva, la probabilidad de conseguir tres veces cara de manera consecutiva es del 12,5%.

A continuación tienes representados todos los eventos posibles junto con sus probabilidades en un diagrama de árbol, de esta forma podrás ver mejor el proceso que hemos seguido para sacar la probabilidad conjunta:

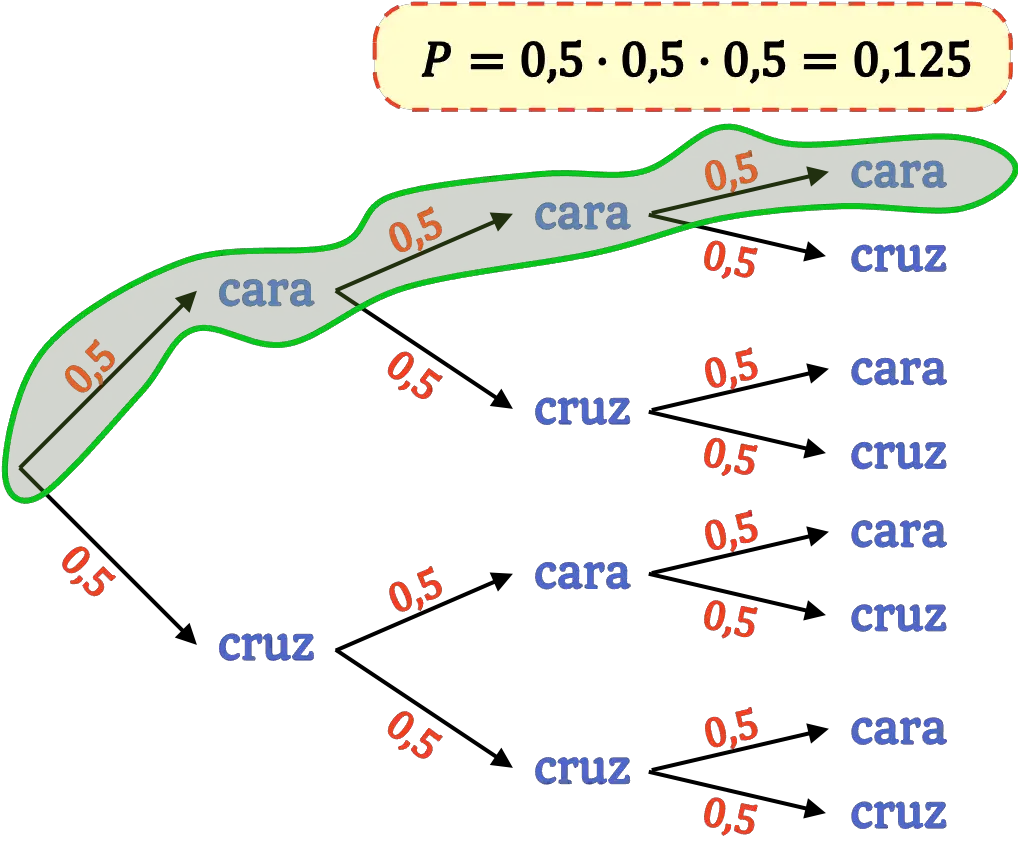
Regla de la multiplicación para eventos dependientes

Ahora que ya hemos visto cuál es la regla de la multiplicación para eventos independientes, vamos a ver cómo es esta ley para eventos dependientes ya que la fórmula varia un poco.

Recuerda que los eventos dependientes son aquellos resultados de un experimento aleatorio cuya probabilidad de ocurrencia dependen entre sí. Es decir, dos eventos son dependientes si la probabilidad de que suceda un evento afecta a la probabilidad de ocurrencia del otro evento.

Fórmula de la regla de la multiplicación para eventos dependientes

Cuando dos eventos son dependientes, la regla de la multiplicación dice que la probabilidad conjunta de que ocurran los dos eventos es igual al producto de la probabilidad de ocurrencia de un evento por la probabilidad condicional del otro evento dado el primer evento.

Así pues, la fórmula de la regla de la multiplicación para eventos dependientes es la siguiente:

P(A\cap B)=P(A)\cdot P(B|A)

Donde:

  • A y B son dos eventos dependientes.
  • P(A\cap B) es la probabilidad de que ocurra el evento A y el evento B.
  • P(A) es la probabilidad de que ocurra el evento A.
  • P(B|A) es la probabilidad condicional de que ocurra el evento B dado el evento A.

Ejemplo de la regla de la multiplicación para eventos dependientes

  • En una caja vacía ponemos 8 bolas azules, 4 bolas naranjas y 2 bolas verdes. Si sacamos primero una bola y después otra bola sin volver a poner la primera bola extraída dentro de la caja, ¿cuál es la probabilidad de que la primera bola sea azul y la segunda bola sea naranja?

En este caso los eventos son dependientes, porque la probabilidad de coger una bola naranja en la segunda extracción depende de qué color sea la bola sacada en la primera extracción. Por lo tanto, para calcular la probabilidad conjunta debemos usar la fórmula de la regla de la multiplicación para eventos dependientes:

P(A\cap B)=P(A)\cdot P(B|A)

La probabilidad de obtener una bola azul en la primera extracción es fácil de determinar, basta con dividir el número de bolas azules por el número total de bolas:

P(\text{bola azul})=\cfrac{8}{8+4+2}=\cfrac{8}{14}=0,57

Por otro lado, la probabilidad de sacar una bola naranja tras haber cogido una bola azul se calcula diferente porque el número de bolas naranjas es distinto y, además, ahora hay una bola menos dentro de la caja:

P(\text{bola naranja}|\text{bola azul})=\cfrac{4}{7+4+2}=\cfrac{4}{13}=0,31

Así pues, la probabilidad conjunta de primero extraer una bola azul y luego una bola naranja se calcula multiplicando las dos probabilidades halladas más arriba:

\begin{array}{l}P(\text{bola azul}\cap\text{bola naranja})=\\[2ex]=P(\text{bola azul})\cdot P(\text{bola naranja}|\text{bola azul})=\\[2ex]=0,57\cdot 0,31= \\[2ex]=0,18\end{array}

Ejercicios resueltos de la regla de la multiplicación

Ejercicio 1

En un pueblo hay solo 3 guarderías: en la guardería A van el 60% de los niños, en la guardería B el 30% y en la guardería C el 10%. Además, en las tres guarderías el 55% de las personas son chicas. Calcula las siguientes probabilidades:

  • Probabilidad de que al seleccionar al azar un niño de la guardería B sea una chica.
  • Probabilidad de que al seleccionar al azar un niño de cualquier guardería sea un chico.

Si la proporción de chicas en todas las guarderías es del 55%, el porcentaje de chicos se calcula simplemente restando 1 menos 0,55:

P(\text{chico})=1-0,55=0,45

Ahora que ya conocemos todas las probabilidades, podemos hacer el diagrama de árbol con las probabilidades de todas las posibilidades:

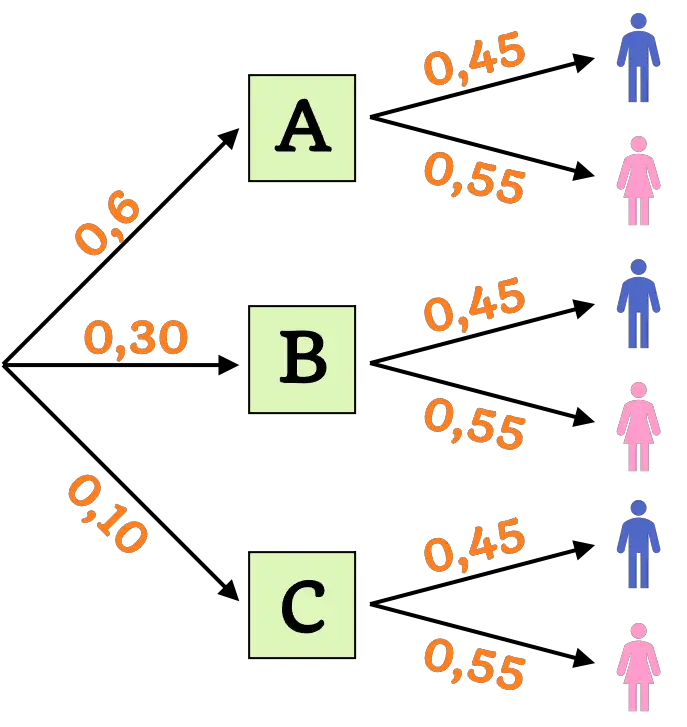
ejercicio resuelto del diagrama de arbol

En este caso los eventos son independientes, pues la probabilidad de que sea chico o chica no depende de la guardería seleccionada. Por lo tanto, para hallar la probabilidad de seleccionar aleatoriamente una chica de la guardería B se debe multiplicar la probabilidad de seleccionar la guardería B por la probabilidad de seleccionar una chica:

P(\text{chica guarder\'ia B})=0,30\cdot 0,55=\bm{0,165}

Por otro lado, para determinar la probabilidad de seleccionar un chico de cualquier guardería primero debemos calcular la probabilidad de escoger un chico para cada guardería y luego sumarlas:

P(\text{chico guarder\'ia A})=0,6\cdot 0,45=0,27

P(\text{chico guarder\'ia B})=0,30\cdot 0,45=0,135

P(\text{chico guarder\'ia C})=0,10\cdot 0,45=0,045

P(\text{chico guarder\'ia A, B o C})=0,27+0,135+0,045=\bm{0,45}

 

Ejercicio 2

Se ha estudiado el ejercicio económico de 25 empresas de un país y cómo evoluciona el precio de sus acciones dependiendo del resultado económico del año. Puedes ver los datos recopilados en la siguiente tabla de contingencia:

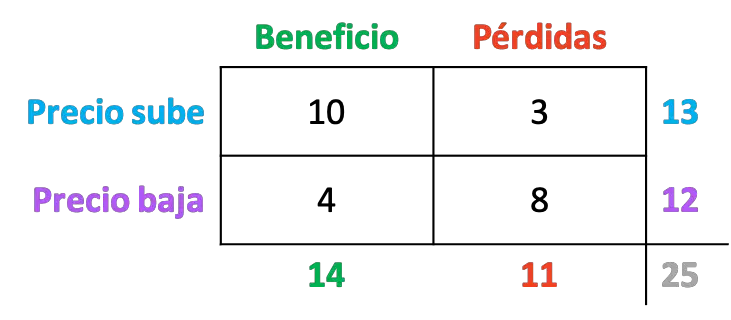
ejercicio resuelto de probabilidad condicionada

¿Cuál es la probabilidad de que una empresa obtenga beneficios y además el precio de sus acciones suba ?

En este caso los eventos son dependientes porque la probabilidad de que las acciones suban o bajen depende del resultado económico. Por lo tanto, tenemos que aplicar la fórmula de la regla de la multiplicación para eventos dependientes:

P(\text{beneficio}\cap\text{precio sube})}=P(\text{beneficio})\cdot P(\text{precio sube}|\text{beneficio})

Así que primero calculamos la probabilidad de que una empresa tengas ganancias y, por otra parte, la probabilidad de que las acciones de la empresa suban cuando ha conseguido un beneficio económico:

P(\text{beneficio})=\cfrac{14}{25}=0,56

P(\text{precio sube}|\text{beneficio})=\cfrac{10}{14}=0,71

Luego sustituimos los valores calculados en la fórmula y hacemos el cálculo de la probabilidad conjunta:

\begin{array}{l}P(\text{beneficio}\cap\text{precio sube})}=\\[2ex]=P(\text{beneficio})\cdot P(\text{precio sube}|\text{beneficio})=\\[2ex]= 0,56\cdot 0,71=\\[2ex] =\bm{0,4} \end{array}

 

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Scroll al inicio