Probabilidad condicional (o probabilidad condicionada)

Aquí encontrarás qué es la probabilidad condicional (o probabilidad condicionada). Te explicamos cómo se calcula la probabilidad condicional con un ejemplo y las propiedades de este tipo de probabilidad. Además, podrás practicar con ejercicios resueltos paso a paso de la probabilidad condicionada.

¿Qué es la probabilidad condicional?

La probabilidad condicional, también llamada probabilidad condicionada, es una medida estadística que indica la probabilidad de que ocurra un evento A si otro evento B ha sucedido. Es decir, la probabilidad condicional P(A|B) se refiere a cuánto de probable es que suceda el evento A una vez ya se ha producido el evento B.

La probabilidad condicional se escribe con una barra vertical entre los dos eventos: P(A|B), y se lee «la probabilidad condicional del evento A dado el evento B».

Ten en cuenta que el valor de la probabilidad condicional es un número entre 0 y 1. Cuanto mayor sea la probabilidad condicional, más probable será de que el evento A se cumpla cuando ocurra el evento B, pero cuanto menor sea la probabilidad condicional, menos probable será que el evento A se cumpla cuando suceda el evento B.

Fórmula de la probabilidad condicional

La probabilidad condicional del evento A dado el evento B es igual a la probabilidad de la intersección entre el evento A y el evento B partido por la probabilidad del evento B.

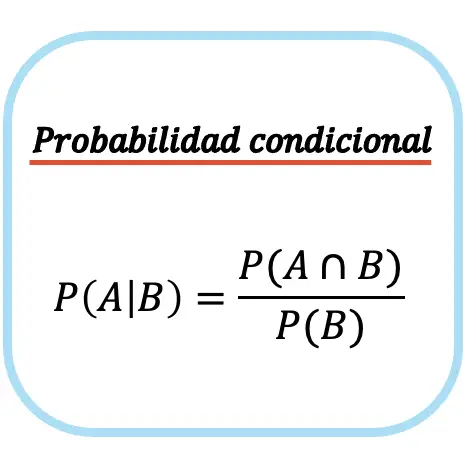
probabilidad condicional o condicionada

Ten en cuenta que la fórmula de la probabilidad condicional (o probabilidad condicionada) solamente se puede utilizar si la probabilidad de ocurrencia del evento no condicionado es diferente de cero, esto es, P(B)≠0. O dicho de otra forma, si es posible que ocurra el evento B.

También se puede calcular la probabilidad condicional a partir de su inversa, es decir, si se conoce P(B|A) se puede determinar P(A|B). Per para ello debes aplicar el teorema de Bayes, puedes consultar en qué consiste este teorema aquí:

Ejemplo de la probabilidad condicional

Una vez hemos visto cuál es la definición y la fórmula de la probabilidad condicional, vamos a resolver paso a paso un ejemplo de este tipo de probabilidad para acabar de entender su significado.

  • Después de haber hecho un examen en una clase de 30 alumnos, se han recogido datos para saber cuántos alumnos han estudiado y cuántos han aprobado, los resultados se muestran en la siguiente tabla de contingencia. A partir de los datos recopilados, calcula la probabilidad condicional de aprobar un examen si has estudiado antes.
ejercicio resuelto de probabilidad condicional

Para sacar la probabilidad condicional debemos aplicar la fórmula que hemos visto antes:

P(\text{aprobado}|\text{estudiado})=\cfrac{P(\text{aprobado}\cap\text{estudiado})}{P(\text{estudiado})}

Por lo tanto, primero debemos hallar la probabilidad de que un alumno haya estudiado y de que un alumno haya estudiado y aprobado. Para encontrar la probabilidad de que un alumno haya estudiado simplemente debemos usar la regla de Laplace, es decir, dividimos el número de alumnos que han estudiado entre el número total de observaciones:

P(\text{estudiado})=\cfrac{23}{30}=0,77

Y la probabilidad de que un alumno haya estudiado y aprobado al mismo tiempo la podemos averiguar a partir de la tabla de contingencia dividiendo el número de alumnos que han estudiado y aprobado entre el total:

P(\text{aprobado}\cap \text{estudiado})=\cfrac{19}{30}=0,63

De modo que la probabilidad de que un alumno apruebe un examen si ha estudiado es:

\begin{aligned}P(\text{aprobado}|\text{estudiado})&=\cfrac{P(\text{aprobado}\cap\text{estudiado})}{P(\text{estudiado})}\\ &=\cfrac{0,63}{0,77}\\[1.5ex] &=0,82\end{aligned}

Probabilidad condicional de eventos dependientes e independientes

En esta apartado veremos cuál es la relación entre la probabilidad condicional y los eventos dependientes e independientes (o sucesos dependientes e independientes). Porque, aunque son conceptos diferentes, estos dos tipos de eventos se relacionan con la probabilidad condicionada.

Dos eventos (o sucesos) son independientes cuando su probabilidad de ocurrencia no dependen entre sí. En tal caso, la intersección entre los dos eventos es equivalente al producto de la probabilidad de cada evento por separado. Y, en consecuencia, la fórmula de la probabilidad condicionada se simplifica:

P(A|B)=\cfrac{P(A\cap B)}{P(B)}=\cfrac{P(A)\cdot P(B)}{P(B)}=P(A)

En definitiva, si los eventos A y B son independientes, la probabilidad condicional del evento A dado el evento B es exactamente igual a la probabilidad de ocurrencia del evento A.

En cambio, cuando dos eventos son dependientes significa que la probabilidad de un evento depende de la probabilidad del otro evento. Por lo tanto, cuando dos eventos A y B son dependientes la probabilidad condicional del evento A dado el evento B es diferente a la probabilidad de ocurrencia del evento A.

P(A|B)\neq P(A)

Ejercicios resueltos de la probabilidad condicional

Ejercicio 1

Se sabe que en una bolsa llena de bolas la mitad son naranjas y la otra mitad son verdes. Además, un tercio de todas las bolas son naranjas y, al mismo tiempo, están marcadas con una señal. ¿Cuál es la probabilidad de que al sacar una bola naranja, esta tenga la señal?

Para resolver el ejercicio tenemos que aplicar la fórmula de la probabilidad condicionada, que es:

P(\text{se\~nal}|\text{naranja})=\cfrac{P(\text{se\~nal}\cap\text{naranja})}{P(\text{naranja})}

El enunciado del problema nos dice que la mitad de la bolsa son naranjas, por tanto, la probabilidad teórica de coger una bola naranja es del 50%.

P(\text{naranja})=\cfrac{1}{2}=0,5

Por otro lado, sabemos que un tercio del total son bolas naranjas y tienen una señal, de manera que la probabilidad de obtener una bola naranja y con señal es:

P(\text{se\~nal}\cap \text{naranja})=\cfrac{1}{3}=0,33

Finalmente, sustituimos las probabilidades calculadas en la fórmula de la probabilidad condicionada para hallar su valor:

\begin{aligned}P(\text{se\~nal}|\text{naranja})&=\cfrac{P(\text{se\~nal}\cap\text{naranja})}{P(\text{naranja})}\\ &=\cfrac{0,33}{0,5}\\[1.5ex] &=0,66\end{aligned}

En resumen, la probabilidad de sacar una bola con la señal si esta es naranja es del 66%.

 

Ejercicio 2

Si en una caja tenemos seis bolígrafos azules y tres bolígrafos negros, calcula la probabilidad de sacar un solo bolígrafo azul y la probabilidad de sacar dos bolígrafos azules consecutivamente.

Para determinar la probabilidad de coger un bolígrafo azul una vez basta con emplear la ley de Laplace:

P(\text{azul})=\cfrac{6}{6+3}=0,67

El problema también nos pide averiguar la probabilidad de coger dos bolígrafos azules consecutivamente, es decir, la probabilidad condicionada de coger un bolígrafo azul si antes ya hemos cogido un bolígrafo azul.

Si sacamos un bolígrafo azul tenemos un caso favorable menos, pero también hay un bolígrafo menos en el total. Por lo tanto, la probabilidad condicional es:

P(\text{azul}|\text{azul})=\cfrac{5}{8}=0,63

 

Ejercicio 3

¿Cuál es la probabilidad condicionada de al tirar un dado obtener el número 4 dado que en el lanzamiento de una moneda salga cara?

Para resolver este ejercicio debes tener en cuenta la teoría de la probabilidad condicional, ya que los eventos «obtener el número 4 del lanzamiento de un dado» y «sacar cara al lanzar una moneda» son independientes. Por lo tanto, no hace falta usar la fórmula de la probabilidad condicional, sino que se cumple la siguiente igualdad:

P(\text{n\'umero 4}|\text{cara})=P(\text{n\'umero 4})

Entonces, para hallar la probabilidad condicional solo tenemos que emplear la regla de Laplace:

P(\text{n\'umero 4}|\text{cara})=P(\text{n\'umero 4})=\cfrac{1}{6}=0,167

 

Ejercicio 4

Se ha estudiado el ejercicio económico de 25 empresas de un país y cómo evoluciona el precio de sus acciones dependiendo del resultado económico del año. Puedes ver los datos recopilados en la siguiente tabla de contingencia:

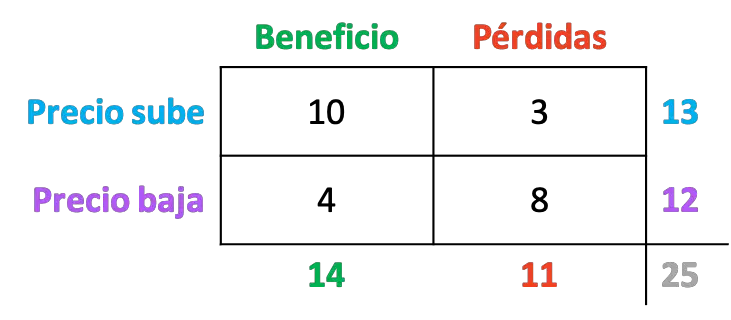
ejercicio resuelto de probabilidad condicionada

¿Cuál es la probabilidad de que el precio de las acciones de una empresa suba si ha obtenido beneficios el último año?

El ejercicio nos pregunta por la probabilidad condicionada de que las acciones suban dado que la empresa haya obtenido un resultado económico positivo. Entonces, para calcular dicha probabilidad, debemos utilizar la fórmula de la probabilidad condicionada:

P(\text{precio sube}|\text{beneficio})=\cfrac{P(\text{precio sube}\cap\text{beneficio})}{P(\text{beneficio})}

Así que primero calculamos la probabilidad de que una empresa tengas ganancias y, por otra parte, la probabilidad de que una empresa obtenga un beneficio económico y al mismo tiempo suba su precio por acción:

P(\text{beneficio})=\cfrac{14}{25}=0,56

P(\text{precio sube}\cap\text{beneficio})=\cfrac{10}{25}=0,4

Y luego sustituimos los valores encontrados en la fórmula y hacemos el cálculo de la probabilidad condicionada:

\begin{aligned}P(\text{precio sube}|\text{beneficio})& =\cfrac{P(\text{precio sube}\cap\text{beneficio})}{P(\text{beneficio})}\\ &= \cfrac{0,4}{0,56}\\[1.5ex]& =0,71 \end{aligned}

 

Propiedades de la probabilidad condicional

Las propiedades de la probabilidad condicional, o probabilidad condicionada, son las siguientes:

  • La suma de la probabilidad condicional del suceso A dado el suceso B más la probabilidad condicional del suceso complementario de A dado el suceso B es igual a uno.

P\bigl(A|B\bigr)+P\bigl(\overline{A}|B\bigr)=1

  • Si el evento A es un subconjunto del evento B, A siempre ocurrirá cuando se cumpla B. De modo que la probabilidad condicionada del evento A dado el evento B en estos casos es 1.

B\subseteq A \ \longrightarrow \ P(A|B)=1

  • Dados dos eventos diferentes, siempre se cumple la siguiente igualdad respecto a la probabilidad condicional:

P\bigl(A\bigr)=P\bigl(A|B\bigr)\cdot P\bigl(B\bigr)+P\bigl(A|\overline{B}\bigl)\cdot P\bigl(\overline{B}\bigr)

11 comentarios en “Probabilidad condicional (o probabilidad condicionada)”

  1. Humberto Garrido

    Agradezco su aportación, me fue de gran ayuda para un trabajo, aprendí mucho del tema además de que está muy bien explicado

    Responder

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Scroll al inicio