En este artículo se explica en qué consiste la estimación por intervalos en estadística. Asimismo, encontrarás cómo se hace la estimación por intervalos y, por último, en qué se diferencia la estimación por intervalos de la estimación puntual.
Índice
¿Qué es la estimación por intervalos?
En estadística, la estimación por intervalos es un proceso en cual se estima el valor de un parámetro poblacional mediante un intervalo. En concreto, la estimación por intervalos consiste en calcular el intervalo en el que es más probable que se encuentre el valor del parámetro con un determinado nivel de confianza.
Por ejemplo, si en una estimación por intervalos se llega a la conclusión de que el intervalo de confianza para la media poblacional es (3,7) con un nivel de confianza del 95%, significa que la media de la población estudiada estará entre 3 y 7 con una probabilidad del 95%.
En general, el tamaño de una población es demasiado grande como para estudiar todos sus individuos, por lo que no se puede conocer el valor de sus medidas estadísticas con certeza, sino que se deber hacer una aproximación.
Así pues, la estimación por intervalos sirve para dar, a partir de los datos muestrales, una aproximación del rango de valores entre los cuales se encuentra el parámetro de la población. De este modo se puede estimar el valor del parámetro poblacional usando los datos estudiados de una muestra.
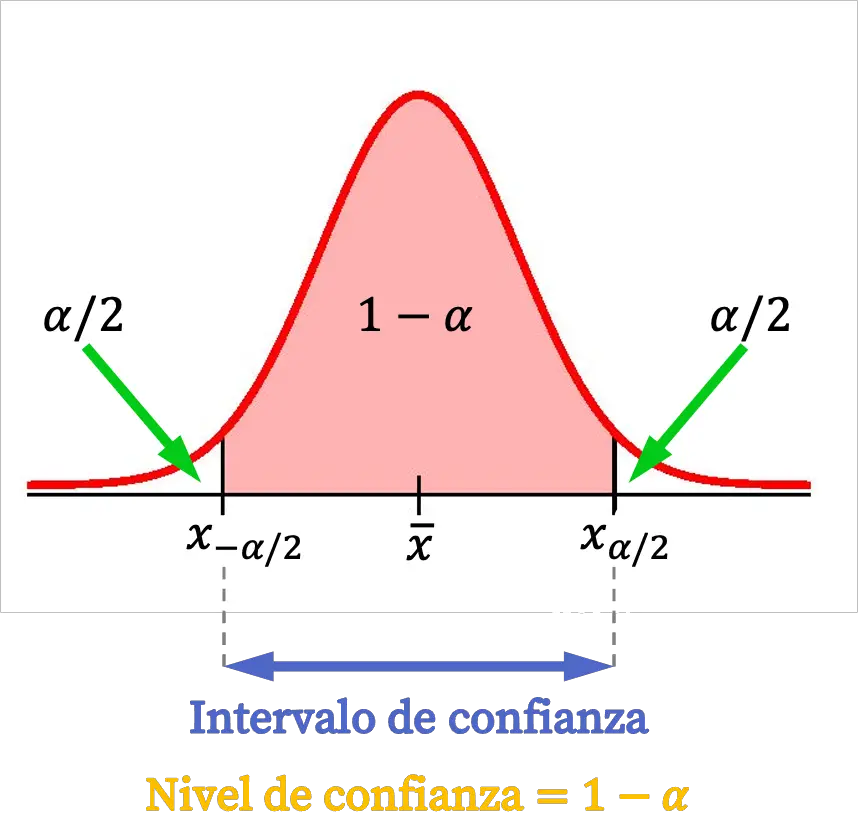
Por último, para acabar de entender el significado de la estimación por intervalos, debes tener claro el concepto de intervalo de confianza. Un intervalo de confianza es el intervalo que proporciona, con un margen de error, una aproximación de los valores entre los cuales se encuentra el valor de un parámetro poblacional. Por lo tanto, el intervalo de confianza es el resultado que se obtiene de una estimación por intervalos.
Fórmulas de la estimación por intervalos
A continuación se muestran las diferentes fórmulas de la estimación por intervalos de confianza, ya que según si se quiere estimar el intervalo de confianza para la media, para la varianza o para la proporción, la fórmula que se debe utilizar es diferente.
Intervalo de confianza para la media
Partiendo de que el proceso de tipificación de una variable se hace de la siguiente manera:

El intervalo de confianza para la media se calcula sumando y restando a la media muestral el valor de Zα/2 multiplicado por la desviación típica (σ) y dividido por la raíz cuadrada del tamaño de la muestra (n). Por lo tanto, la fórmula para calcular el intervalo de confianza para la media es la siguiente:

Para tamaños muestrales grandes y un nivel de confianza del 95% el valor crítico es Zα/2=1,96 y para un nivel de confianza del 99% el valor crítico es Zα/2=2,576.
La fórmula anterior se utiliza cuando la varianza de la población es conocida. No obstante, si la varianza de la población es desconocida, que es el caso más frecuente, el intervalo de confianza para la media se calcula con la siguiente fórmula:

Donde:
 es la media de la muestra.
es la media de la muestra. es el valor de la distribución t de Student de n-1 grados de libertad con una probabilidad de α/2.
es el valor de la distribución t de Student de n-1 grados de libertad con una probabilidad de α/2. es la desviación típica de la muestra.
es la desviación típica de la muestra. es el tamaño de la muestra.
es el tamaño de la muestra.
Intervalo de confianza para la varianza
Para calcular el intervalo de confianza para la varianza de una población se utiliza la distribución chi-cuadrado. En concreto, la fórmula para calcular el intervalo de confianza para la varianza es la siguiente:

Donde:
 es el tamaño de la muestra.
es el tamaño de la muestra. es la desviación típica de la muestra.
es la desviación típica de la muestra. es el valor de la distribución chi-cuadrado con n-1 grados de libertad para una probabilidad inferior a α/2.
es el valor de la distribución chi-cuadrado con n-1 grados de libertad para una probabilidad inferior a α/2. es el valor de la distribución chi-cuadrado con n-1 grados de libertad para una probabilidad superior a 1-α/2.
es el valor de la distribución chi-cuadrado con n-1 grados de libertad para una probabilidad superior a 1-α/2.
Intervalo de confianza para la proporción
El intervalo de confianza para la proporción se calcula sumando y restando a la proporción de la muestra el valor de Zα/2 multiplicado por la raíz cuadrada de la proporción muestral (p) multiplicado por 1-p y divido por el tamaño de la muestra (n). Por lo tanto, la fórmula para calcular el intervalo de confianza para la proporción es la siguiente:

Donde:
 es la proporción de la muestra.
es la proporción de la muestra. es el tamaño de la muestra.
es el tamaño de la muestra. es el cuantil de la distribución normal estándar correspondiente a una probabilidad de α/2. Para tamaños muestrales grandes y un nivel de confianza del 95% se suele aproximar a 1,96 y para una confianza del 99% se suele aproximar a 2,576.
es el cuantil de la distribución normal estándar correspondiente a una probabilidad de α/2. Para tamaños muestrales grandes y un nivel de confianza del 95% se suele aproximar a 1,96 y para una confianza del 99% se suele aproximar a 2,576.
Estimación por intervalos y estimación puntual
Finalmente, veremos cuáles son las diferencias entre la estimación por intervalos y la estimación puntual, pues el valor de un parámetro poblacional se puede estimar mediante un intervalo (tal y como hemos visto a lo largo del post) o mediante un valor puntual.
La diferencia entre la estimación por intervalos y la estimación puntual es el rango de valores que se usan en la estimación del parámetro. En la estimación por intervalos se aproxima un parámetro a un intervalo de confianza, mientras que en la estimación puntual se aproxima el parámetro a un valor concreto.
Por lo tanto, en la estimación puntual se toma un valor único, calculado a partir de los datos de la muestra, como aproximación del valor del parámetro de la población. Por ejemplo, la media poblacional se puede estimar puntualmente mediante la media muestral.
Así pues, la estimación puntual tiene una ventajas y unas desventajas respecto a la estimación por intervalos, de manera que cada tipo de estimación es adecuada usarla en una situación determinada. Para saber más al respecto, haz clic en el siguiente enlace:
