En este post se explica qué es el intervalo de confianza para la media en estadística y para qué sirve. Asimismo, encontrarás cómo calcular el intervalo de confianza para la media junto con un ejercicio resuelto paso a paso.
Índice
¿Qué es el intervalo de confianza para la media?
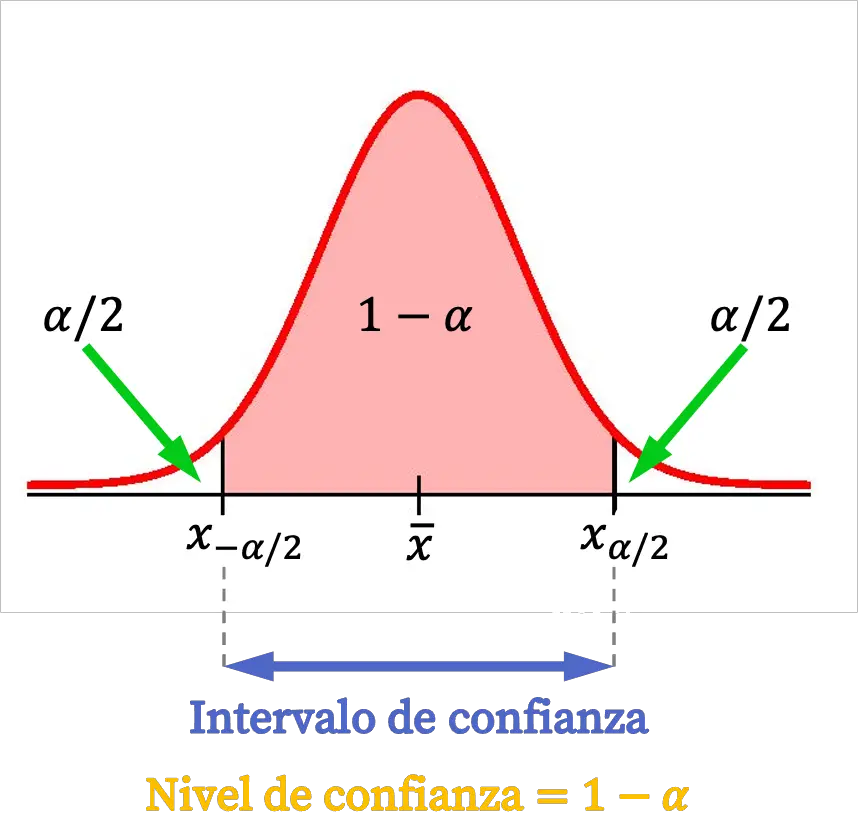
El intervalo de confianza para la media es un intervalo que proporciona un rango de valores admisibles para la media de una población. Es decir, el intervalo de confianza para la media nos da un valor máximo y un valor mínimo entre los cuales se encuentra el valor de la media de una población con un margen de error.
Por ejemplo, si el intervalo de confianza del 95% para la media de una población es (6,10), significa que el 95% de veces la media poblacional estará entre 6 y 10.
Por lo tanto, el intervalo de confianza para la media se usa para estimar dos valores entre los cuales se encuentra la media de una población. Así pues, el intervalo de confianza para la media resulta muy útil para aproximar el promedio de una población cuando se desconocen todos sus valores.
Fórmula del intervalo de confianza para la media
Partiendo de que el proceso de tipificación de una variable se hace de la siguiente manera:

El intervalo de confianza para la media se calcula sumando y restando a la media muestral el valor de Zα/2 multiplicado por la desviación típica (σ) y dividido por la raíz cuadrada del tamaño de la muestra (n). Por lo tanto, la fórmula para calcular el intervalo de confianza para la media es la siguiente:

Para tamaños muestrales grandes y un nivel de confianza del 95% el valor crítico es Zα/2=1,96 y para un nivel de confianza del 99% el valor crítico es Zα/2=2,576.
La fórmula anterior se utiliza cuando la varianza de la población es conocida. No obstante, si la varianza de la población es desconocida, que es el caso más frecuente, el intervalo de confianza para la media se calcula con la siguiente fórmula:

Donde:
 es la media de la muestra.
es la media de la muestra. es el valor de la distribución t de Student de n-1 grados de libertad con una probabilidad de α/2.
es el valor de la distribución t de Student de n-1 grados de libertad con una probabilidad de α/2. es la desviación típica de la muestra.
es la desviación típica de la muestra. es el tamaño de la muestra.
es el tamaño de la muestra.
Ejemplo del cálculo de un intervalo de confianza para la media
Para que puedas ver cómo se calcula el intervalo de confianza para la media de una población, a continuación te dejamos con un ejemplo resuelto paso a paso.
- Tenemos una muestra de 8 observaciones con los valores mostrados a continuación. ¿Cuál es el intervalo de confianza para la media de la población con un nivel de confianza del 95%?
206 203 201 212
194 176 208 201
Tal y como hemos visto en el apartado anterior, la fórmula que nos permite sacar el intervalo de confianza para una media poblacional cuando no conocemos la desviación típica de la población es la siguiente:

Entonces, para poder determinar el intervalo de confianza de la media, primero tenemos que calcular la media y la desviación típica de la muestra.
![Rendered by QuickLaTeX.com \begin{array}{c}\mu =200,13 \\[4ex]s=11,13\end{array}](http://www.probabilidadyestadistica.net/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)
Como queremos hallar el intervalo de confianza con un nivel de confianza de 1-α=95% y el tamaño muestral es 8, tenemos que ir a la tabla de la distribución t de Student y ver qué valor corresponde a t0,025|7.
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}t_{\alpha/2| n-1}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 7}=2,365\end{array}](http://www.probabilidadyestadistica.net/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)
De modo que aplicamos la fórmula del intervalo de confianza para la media y hacemos los cálculos para encontrar los valores límites del intervalo:


![]()
En conclusión, el intervalo de confianza calculado nos indica que con un nivel de confianza del 95% la media de la población estará entre 190,82 y 209,43.

BIEN EXPLICADO
¡Muchas gracias Felix!