Aquí encontrarás qué son los cuantiles y cómo se calculan. También te explicamos cuáles son los tipos de cuantiles y podrás ver ejemplos resueltos del cálculo de cuantiles. Por último, podrás calcular cualquier cuantil de tu muestra de datos con una calculadora online.
Índice
¿Qué son los cuantiles?
En estadística, los cuantiles son puntos que dividen un conjunto de datos ordenados en partes iguales. De modo que un cuantil indica el valor por debajo del cual se encuentra un porcentaje de datos.
Por ejemplo, si el valor del cuantil de orden 0,39 es 24, significa que el 39% de los datos de la muestra son menores que 24 y que el resto de datos son mayores que 24.
Por lo tanto, los cuantiles sirven para separar los datos de una distribución en grupos iguales. Además, también se usan para indicar el porcentaje de datos mayor o menor que un determinado valor.
👉 Puedes usar la calculadora que hay más abajo para calcular los cuantiles de cualquier conjunto de datos.
Tipos de cuantiles
Los diferentes tipos de cuantiles son:
- Cuartiles: cuantiles que dividen el conjunto de datos en cuatro partes iguales. Por lo tanto, hay tres cuartiles: el primer cuartil (Q1), el segundo cuartil (Q2) y el tercer cuartil (Q3).
- Quintiles: cuantiles que dividen el conjunto de datos en cinco partes iguales. De manera que en una muestra solo pueden haber cuatro quintiles. Este tipo de cuantiles se expresan mediante la letra K.
- Deciles: cuantiles que dividen el conjunto de datos en diez partes iguales. El símbolo de los deciles es la letra D.
- Percentiles: cuantiles que dividen el conjunto de datos en cien partes iguales. Los percentiles también indican un porcentaje de la muestra. Se denominan con la letra P.
Una de las propiedades que relaciona los distintos tipos de cuantiles es que la mediana, el segundo cuartil, el quinto decil y el percentil 50 tienen el mismo valor.
Además, también existen otros tipos de cuantiles pero estos se utilizan menos. Entre ellos destacan los terciles, que dividen un serie de datos en tres partes idénticas, y los vigentiles, que separan los datos recopilados en veinte trozos equivalentes.
Asimismo, todos los tipos de cuantiles se consideran medidas de posición no centrales.
Cómo calcular cuantiles
Para calcular la posición de un cuantil de un conjunto de datos estadísticos debes multiplicar el número del cuantil por la suma del número total de datos más uno.
De modo que la fórmula de los cuantiles es:
![]()
Atención: esta fórmula nos indica la posición del cuantil, no su valor. El cuantil será el dato situado en la posición obtenida por la fórmula.
Sin embargo, a veces el resultado de esta fórmula nos dará un número decimal. De manera que debemos distinguir dos casos dependiendo de si el resultado es un número decimal o no:
- Si el resultado de la fórmula es un número sin parte decimal, el cuantil es el dato que está en la posición que nos proporciona la fórmula de arriba.
- Si el resultado de la fórmula es un número con parte decimal, el valor exacto del cuantil se calcula mediante la siguiente fórmula:
![]()
Donde xi y xi+1 son los números de las posiciones entre las cuales está el número obtenido por la primera fórmula, y d es la parte decimal del número obtenido por la primera fórmula.
Si estás pensando que el cálculo de un cuantil es muy complicado, no te preocupes. Lee los siguientes ejemplos y verás que en realidad es sencillo.
Nota: en la comunidad científica aún no existe un consenso sobre el cálculo de los cuantiles, así que puede que encuentres algún libro de estadística que lo explique un poco diferente.
Ejemplos del cálculo de cuantiles
Vista la definición de cuantil y la teoría de cómo se calcula, a continuación tienes un ejercicio resuelto sobre el cálculo de unos cuantiles. Así podrás entender mejor el concepto.
- Calcula el cuantil de orden 0,50 y el cuantil de orden 0,81 de la siguiente muestra estadística.

Los datos del problema ya están ordenados de manera ascendiente, por lo que no es necesario modificarlos. De lo contrario, primero tendríamos que haber puesto los datos por orden.
Tal y como se ha explicado más arriba, la fórmula que nos permite encontrar la posición de cualquier cuantil es la siguiente:
![]()
En este caso, tamaño muestral es de 49 observaciones, por lo tanto, para calcular el cuantil 0,50 tenemos que sustituir la n por 49 y la p por 0,50:
![]()
De manera que el cuantil 0,50 será aquel valor que esté en la vigesimoquinta posición de la lista ordenada, que corresponde al valor 250.
Ahora volvemos a aplicar la misma fórmula para hallar el cuantil 0,81. Lógicamente, en este segundo ejemplo debemos sustituir la p por 0,81.
![]()
Pero esta vez hemos obtenido un número decimal de la fórmula (40,5), lo que significa que el cuantil estará entre la posición 40 y la posición 41. Por lo tanto, para determinar este cuantil debemos usar la segunda fórmula del método:
![]()
En este caso el cuantil estará entre los posiciones 40 y 41, cuyos valores son respectivamente 286 y 289. Por lo tanto, xi es 286, xi+1 es 289, y d es la parte decimal del número obtenido, esto es, 0,5.
![]()
Como puedes ver, el cálculo de un cuantil depende de si la primera fórmula nos da un número decimal o no. Por si quieres ver más ejemplos, puedes ver más ejercicios resueltos de los diferentes tipos de cuantiles aquí:
➤ Ver: ejemplos de quintiles
➤ Ver: ejemplos de deciles
➤ Ver: ejemplos de percentiles
Calculadora de cuantiles
Introduce un conjunto de datos estadísticos y el número de cuantil que quieres calcular en la siguiente calculadora. Los números deben separase por un espacio e introducirse usando el punto como separador decimal.
Cuantiles en datos agrupados
Para calcular un cuantil cuando los datos están agrupados en intervalos primero debemos encontrar el intervalo o clase en el que se encuentra el cuantil utilizando la siguiente fórmula:
![]()
De manera que el cuantil estará en el intervalo cuya frecuencia absoluta acumulada sea inmediatamente superior al número obtenido en la expresión anterior.
Y una vez sabemos el intervalo al que pertenece el cuantil, tenemos que aplicar la siguiente fórmula para hallar el valor exacto del cuantil:

Donde:
- Li es el límite inferior del intervalo en el que se halla el cuantil.
- n es el número total de observaciones.
- Fi-1 es la frecuencia absoluta acumulada del intervalo anterior.
- fi es la frecuencia absoluta del intervalo en el que se encuentra el cuantil.
- Ii es la amplitud del intervalo del cuantil.
Para que veas cómo se hace, a continuación tienes un ejemplo resuelto del cálculo de los cuantiles de orden 0,29 y 0,62 para datos agrupados.
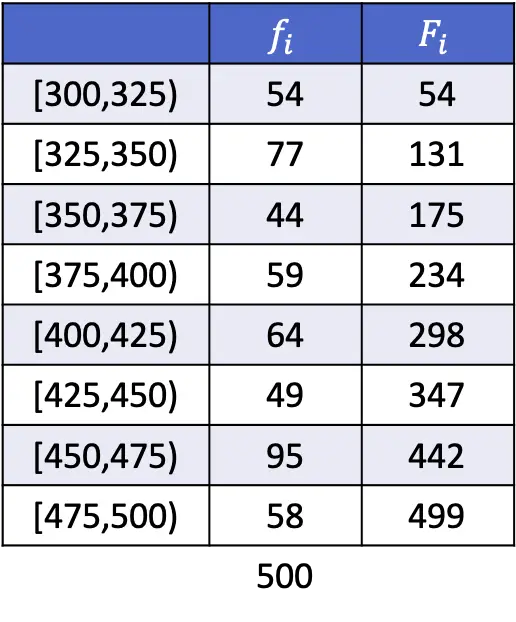
Para hacer el cálculo del cuantil 0,29 primero debemos encontrar el intervalo en el que se encuentra. Para ello, utilizamos la siguiente fórmula:
![]()
![]()
De manera que el cuantil estará en el intervalo cuya frecuencia absoluta acumulada sea inmediatamente superior a 145,29, que en este caso es el intervalo [350,375) cuya frecuencia absoluta acumulada es 175. Y una vez sabemos el intervalo del cuantil, empleamos la segunda fórmula del método:

![]()
Ahora volvemos a aplicar el mismo procedimiento para sacar el cuantil 0,62. Primero calculamos el intervalo donde está el cuantil:
![]()
El intervalo cuya frecuencia absoluta acumulada es inmediatamente superior a 310,62 es [425,450), con una frecuencia absoluta acumulada de 347. Por lo tanto, el valor exacto del cuantil lo calculamos utilizando la segunda fórmula del proceso::
![]()
