Deciles

En este artículo te explicamos qué son los deciles y cómo se calculan. También encontrarás varios ejemplos resueltos paso a paso del cálculos de los deciles y, además, podrás calcular los deciles de cualquier muestra estadística con una calculadora online.

¿Qué son los deciles?

En estadística, los deciles son los nueve valores que dividen a un conjunto de datos ordenados en diez partes iguales. De modo que el primer, segundo, tercer… decil representa el 10%, 20%, 30%… de la muestra o población.

Por ejemplo, el valor del cuarto decil es más grande que el 40% los datos, pero más pequeño que el resto de los datos.

Los deciles se representan mediante la letra D mayúscula y el subíndice del decil, es decir, el primer decil es D₁, el segundo decil es D₂, el tercer decil es D₃, etc.

👉 Puedes usar la calculadora que hay más abajo para calcular los deciles de cualquier conjunto de datos.

Cabe destacar que los deciles son una medida de posición no central junto a los cuartiles, los quintiles y los percentiles. Puedes consultar qué significa cada uno de estos tipos de cuantiles en nuestra página web.

Además, el quinto decil es equivalente a la mediana y al segundo cuartil, ya que dividen el conjunto de datos en dos partes iguales.

Cómo calcular los deciles

Para calcular la posición de los deciles de una serie de datos estadísticos debes multiplicar el número del decil por la suma del número total de datos más uno y dividir el resultado entre diez.

Por lo tanto, la fórmula de los deciles es:

Atención: esta fórmula nos indica la posición del decil, no el valor del decil. El decil será el dato situado en la posición obtenida por la fórmula.

Sin embargo, a veces el resultado de esta fórmula nos dará un número decimal, por lo que debemos distinguir dos casos dependiendo de si el resultado es un número decimal o no:

• Si el resultado de la fórmula es un número sin parte decimal, el decil es el dato que está en la posición que nos proporciona la fórmula de arriba.
• Si el resultado de la fórmula es un número con parte decimal, el valor del decil se calcula mediante la siguiente fórmula:

Donde x_i y x_i+1 son los números de las posiciones entre las cuales está el número obtenido por la primera fórmula, y d es la parte decimal del número obtenido por la primera fórmula.

Puede que ahora pienses que sacar los deciles de una muestra estadística es complejo, pero a la práctica es bastante sencillo. Si lees los siguientes dos ejemplos seguro que lo entiendes mucho mejor.

Nota: la comunidad científica no está totalmente de acuerdo en el cálculo de los deciles, de modo que puede que encuentres algún libro de estadística que lo explique un poco diferente.

Ejemplo del cálculo de deciles

Como has visto arriba, el cálculo de los deciles depende de si el número que nos da la primera fórmula es decimal o no, por ese motivo te hemos preparado dos ejemplos resueltos a continuación, uno para cada caso. De todos modos, recuerda que si te queda alguna duda de cómo se hallan los deciles puedes preguntar en los comentarios.

Ejemplo 1

• Dados los siguientes datos ordenados de menor a mayor, halla el primer, el tercer y el octavo decil de la muestra.

Los datos de este ejercicio ya están ordenados así que no es necesario cambiarlos de orden, de lo contrario, primero tendríamos que ordenar los datos de menor a mayor.

Tal y como se explica arriba, la fórmula que nos permite encontrar las posiciones de los deciles es la siguiente:

El tamaño de la muestra de este ejercicio es de 29 observaciones, por lo tanto, para calcular la posición del primer decil debemos sustituir la n por 29 y la k por 1:

El resultado de la fórmula es un 3, por lo que el primer decil estará en la tercera posición de la lista ordenada, y ese valor corresponde a 85.

Ahora volvemos a aplicar el mismo procedimiento pero con el tercer decil. Usamos la fórmula sustituyendo la k por un 3:

De manera que el tercer decil será el elemento en la novena posición, esto es, el 97.

Por último, hacemos el mismo proceso pero poniendo un 8 en la fórmula para determinar el octavo decil:

El octavo decil será el número en la posición 24 de la lista ordenada de los datos, por lo que el octavo decil es el 131.

Ejemplo 2

• A partir de los datos de la siguiente tabla, calcula los deciles 4, 7 y 9.

Al igual que en el ejemplo anterior, para obtener las posiciones de los deciles debemos utilizar la siguiente fórmula:

En este caso el tamaño muestral es 42, por lo que para hallar la posición del cuarto decil tenemos que sustituir el parámetro n por 42 y la k por 4:

Pero esta vez hemos obtenido un número decimal de la fórmula, por lo tanto, tenemos que aplicar la siguiente fórmula para calcular el decil exacto:

El número obtenido de la primera fórmula es 17,2, de modo que el cuarto decil está entre el decimoséptimo y el decimoctavo dato, que son respectivamente 109 y 112. Por lo tanto, x_i es 109, x_i+1 es 112, y d es la parte decimal del número obtenido, esto es, 0,2.

Repetimos el mismo proceso para encontrar el séptimo decil. Primero calculamos la posición del decil:

De la fórmula hemos obtenido el número 30,1, lo que significa que el decil estará entre la posición 30 y 31, cuyos valores son 154 y 159. De modo que el cálculo del decil exacto es:

Finalmente, volvemos a aplicar el mismo método para sacar el noveno decil. Determinamos la posición del decil:

El número obtenido es decimal y está entre el 38 y el 39, cuyas posiciones corresponden a los valores 189 y 196. De manera que el cálculo del decil 9 es:

Calculadora de deciles

Introduce un conjunto de datos estadísticos en la siguiente calculadora para calcular los deciles. Los datos deben separase por un espacio e introducirse usando el punto como separador decimal.

Deciles en datos agrupados

Para calcular los deciles cuando los datos están agrupados en intervalos, primero debemos encontrar el intervalo o clase en el que se encuentra el decil utilizando la siguiente fórmula:

De modo que el decil estará en el intervalo cuya frecuencia absoluta sea inmediatamente superior al número obtenido en la expresión anterior.

Y una vez ya sabemos el intervalo al que pertenece el decil, tenemos que aplicar la siguiente fórmula para hallar el valor exacto del decil:

Donde:

• L_i es el límite inferior del intervalo en el que se halla el decil.
• n es el número total de datos estadísticos.
• F_i-1 es la frecuencia absoluta acumulada del intervalo anterior.
• f_i es la frecuencia absoluta del intervalo en el que se encuentra el decil.
• I_i es la amplitud del intervalo del decil.

Para que puedas ver cómo se hace, a continuación tienes un ejercicio resuelto en el que se calculan los deciles 3, 5 y 8 de los siguientes datos agrupados por intervalos.

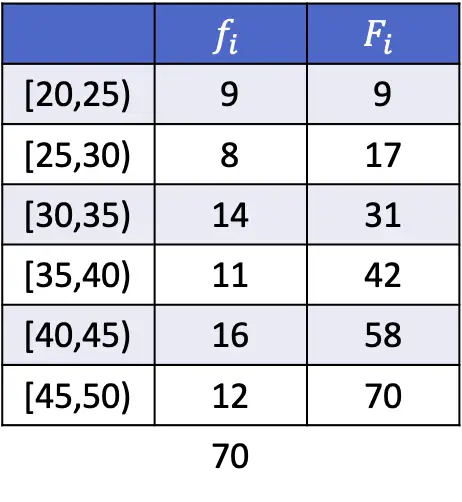
Como los datos están agrupados, el cálculo de cada decil consiste en dos pasos: primero se debe encontrar el intervalo en el que se encuentra el decil, y luego se calcula el valor exacto del decil. Entonces, encontramos el intervalo del tercer decil:

El intervalo del decil será aquel cuya frecuencia absoluta acumulada sea inmediatamente superior a 21,3, y en este caso es el intervalo [30,35) cuya frecuencia absoluta acumulada es 31. Ahora que ya sabemos el intervalo del decil, aplicamos la siguiente fórmula para hallar el valor exacto del decil:

Ahora tenemos que volver a aplicar el método para sacar el quinto decil. Primero determinamos el intervalo en que se encuentra:

El resultado 35 significa que está en el intervalo [35,40) pero no porque haya un 35 en la expresión del intervalo, sino porque su frecuencia absoluta acumulada (42) es la inmediatamente superior. Y una vez está localizado el intervalo, aplicamos la segunda fórmula del proceso:

Finalmente, hallamos el octavo decil. Para ello, primero hacemos el cálculo de su intervalo:

La frecuencia absoluta acumulada inmediatamente superior a 56,8 es 58, por lo que el intervalo del octavo decil es [40,45). De modo que solo nos queda determinar el valor exacto del decil: