En este post encontrarás en qué consiste la asimetría negativa, un ejemplo de una distribución con asimetría negativa y cuál es el cálculo que se debe hacer para saber si una distribución es asimétrica negativa.
Índice
¿Qué es la asimetría negativa?
En estadística, se dice que una distribución tiene asimetría negativa cuando su gráfica tiene la cola de la izquierda más larga que la de la derecha.
Es decir, una distribución asimétrica negativa significa que tiene más valores distintos a la izquierda de la media.
La definición de asimetría negativa puede parecer subjetiva, sin embargo se puede saber si una distribución de probabilidad es asimétrica negativa o no mediante una fórmula. Más abajo veremos cómo se hace.
Ejemplo de asimetría negativa
A continuación puedes ver un ejemplo de asimetría negativa para entender mejor el concepto:
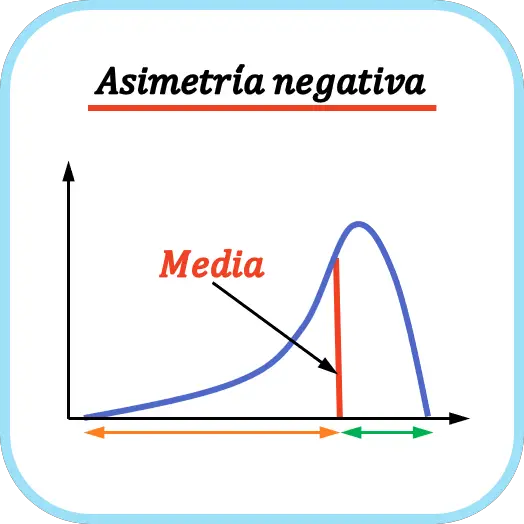
Si te fijas en la gráfica, hay más valores a la izquierda de la media que a su derecha, por lo tanto, la curva tiene asimetría negativa.
Asimetría negativa y asimetría positiva
Dos tipos de simetrías habituales en las distribuciones de probabilidad son la asimetría negativa y la asimetría positiva, por eso en esta sección veremos en qué se diferencia su significado.
La diferencia entre la asimetría negativa y la asimetría positiva es el lado de la media en el que hay más valores. Una distribución asimétrica negativa tiene más valores distintos a la izquierda de la media, en cambio, una distribución es asimétrica positiva cuando tiene más valores distintos a la derecha de la media.
Por otro lado, una distribución es simétrica cuando hay el mismo número de valores a la izquierda que a la derecha de la media.
Cómo determinar la asimetría negativa
Tradicionalmente, se ha explicado que si la media es menor que la mediana, la distribución posee asimetría negativa. Sin embargo, esta propiedad no se cumple siempre. Así que para determinar la asimetría de una distribución se debe calcular el coeficiente de asimetría de Fisher.
El coeficiente de asimetría de Fisher se calcula mediante la siguiente fórmula:
![\displaystyle\gamma_1=E\left[\left(\frac{X-\mu}{\sigma}\right)^3 \right]](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-84760f654e2f90388307dc01a2dbbede_l3.svg "Rendered by QuickLaTeX.com")
O, equivalentemente:
![\displaystyle\gamma_1=\frac{\operatorname{E}[X^3] - 3\mu\sigma^2 - \mu^3}{\sigma^3}](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-18401d04862cb735b0016b09d4282b90_l3.svg "Rendered by QuickLaTeX.com")
Donde 
es la esperanza matemática, 
la media aritmética y 
la desviación estándar.
El signo del coeficiente de Fisher permite determinar la asimetría de la distribución:
- Si el coeficiente de asimetría de Fisher es negativo, la distribución es asimétrica negativa.
- Si el coeficiente de asimetría de Fisher es positivo, la distribución es asimétrica positiva.
- Si la distribución es simétrica, el coeficiente de asimetría de Fisher es igual a cero (el recíproco no es cierto).
