▷ Desviación estándar (o desviación típica)

En este artículo se explica qué es la desviación estándar, también conocida como desviación típica. Encontrarás cómo calcular la desviación estándar, un ejemplo resuelto paso a paso, y una calculadora online para encontrar la desviación estándar de cualquier muestra de datos.

Índice

¿Qué es la desviación estándar (o desviación típica)?

La desviación estándar, también llamada desviación típica, es una medida de dispersión estadística. Es decir, la desviación estándar es un valor que indica la dispersión de un conjunto de datos estadísticos.

Por lo tanto, la desviación estándar (o desviación típica) sirve para cuantificar la dispersión de una población o muestra estadística. Cuanto mayor sea la desviación estándar de una serie de datos, significa que más dispersos están los datos. Y la interpretación también se puede hacer al revés, si la desviación estándar es baja quiere decir que en general los datos están muy cerca de su media.

Cuando se calcula la desviación estándar o típica sobre una población, el símbolo de la desviación estándar es la letra griega sigma (σ). Pero cuando es una desviación estándar muestral, se utiliza la letra s para representar la medida estadística.

En algunos libros de estadística y probabilidad la desviación estándar también se llama desvío típico.

Fórmula de la desviación estándar (o desviación típica)

La desviación estándar (o desviación típica) es igual a la raíz cuadrada de la suma de los cuadrados de las desviaciones de la serie de datos partido por el número total de observaciones.

De modo que la fórmula para calcular la desviación estándar (o desviación típica) es:

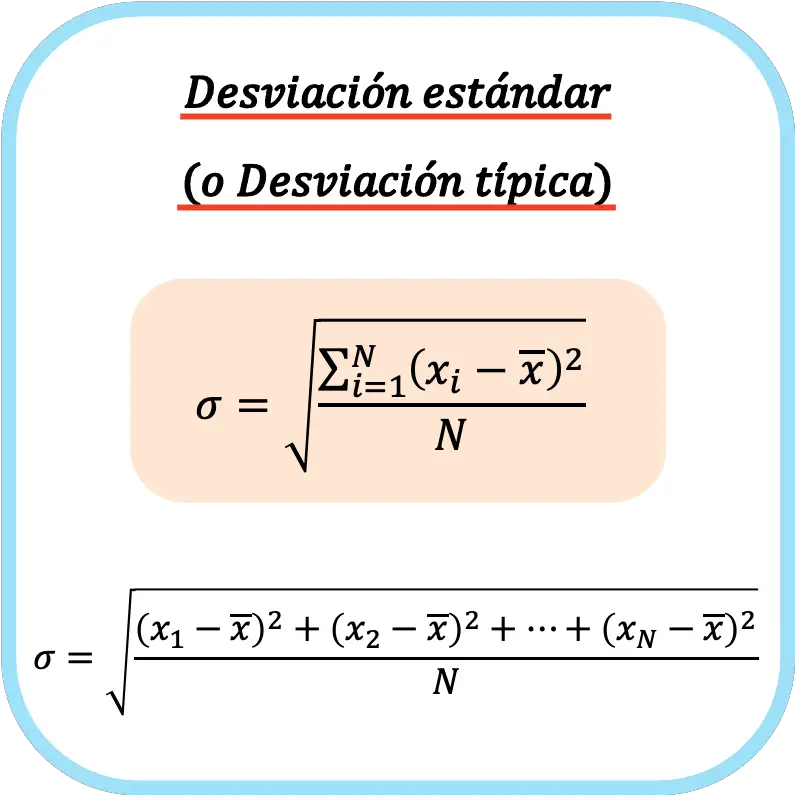
👉 Puedes usar la calculadora que hay más abajo para calcular la desviación estándar de cualquier conjunto de datos.

En conclusión, para hallar la desviación estándar de un conjunto de datos se deben calcular todas las desviaciones (definidas como la diferencia entre un dato y la media aritmética), elevar a la dos las desviaciones, sumarlas todas, luego dividir entre el número total de datos, y finalmente sacar la raíz cuadrada.

Ejemplo de desviación estándar (o desviación típica)

Vista la definición de desviación estándar (o desviación típica), a continuación tienes un ejemplo resuelto paso a paso para que veas cómo se calcula la desviación estándar de una serie de datos.

Calcula la desviación estándar de los siguientes valores: 3, 6, 2, 9, 4.

Lo primero que debemos hacer es determinar el promedio de la muestra. Para ello, sumamos todos los datos y dividimos entre el número total de observaciones, que es cinco:

$\overline{x}=\cfrac{3+6+2+9+4}{5}=4,8$

Ahora usamos la fórmula de la desviación estándar:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N(x_i-\overline{x})^2}{N}}$

Sustituimos los datos en la fórmula:

$\displaystyle\sigma =\sqrt{\frac{(3-4,8)^2+(6-4,8)^2+(2-4,8)^2+(9-4,8)^2+(4-4,8)^2}{5}}$

Y finalmente hacemos el cálculo de la desviación estándar:

$\begin{aligned}\displaystyle\sigma & = \sqrt{\frac{(-1,8)^2+1,2^2+(-2,8)^2+4,2^2+(-0,8)^2}{5}}\\[2ex]&=\sqrt{\frac{3,24+1,44+7,84+17,64+0,64}{5}}\\[2ex]&= \sqrt{\frac{30,8}{5}}=\sqrt{6,16}=2,48 \end{aligned}$

Calculadora de la desviación estándar (o desviación típica)

Introduce un conjunto de datos estadísticos en la siguiente calculadora online para calcular su desviación estándar (o desviación típica). Los datos deben separase por un espacio e introducirse usando el punto como separador decimal.

Desviación estándar (o típica) para datos agrupados

Para calcular la desviación estándar (o desviación típica) de unos datos agrupados en intervalos, se deben hacer los siguientes pasos:

Hallar la media de los datos agrupados.
Calcular las desviaciones de los datos agrupados.

Elevar cada desviación al cuadrado.
Multiplicar cada resultado anterior por la frecuencia de su intervalo.
Hacer el sumatorio de todos los valores obtenidos en el paso anterior.

Dividir entre el número total de observaciones.
Sacar la raíz cuadrada del valor anterior. El número obtenido es la desviación estándar de los datos agrupados.

En conclusión, la fórmula para calcular la desviación estándar de unos datos agrupados en intervalos es:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N\left(x_i-\overline{x}\right)^2\cdot f_i }{N}}$

Aunque normalmente se utiliza la fórmula de arriba, también se puede usar la siguiente expresión algebraica ya que se obtiene el mismo resultado:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^n x_i^2\cdot f_i }{N}-\overline{x}^2}$

Para que puedas ver cómo se hace, a continuación tienes un ejercicio resuelto paso a paso de la desviación estándar de unos datos agrupados en intervalos. En concreto, se calculará la desviación estándar de los siguientes datos estadísticos:

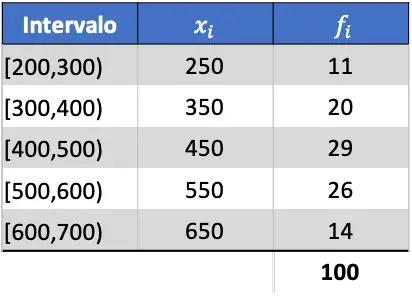
ejemplo de datos agrupados en intervalos

En primer lugar, multiplicamos la marca de clase de cada intervalo por su frecuencia para poder hacer el cálculo de la media aritmética:

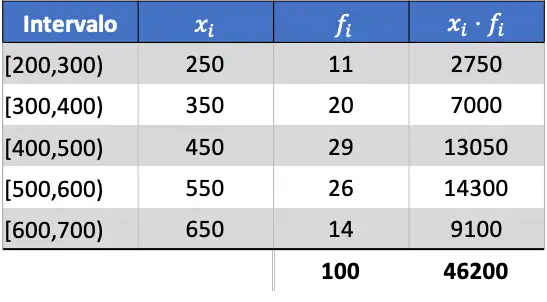
De manera que la media de los datos agrupados será:

$\overline{x}=\cfrac{\displaystyle\sum_{i=1}^n x_i\cdot f_i}{N}=\cfrac{46200}{100}=462$

Ahora que ya conocemos el valor de la media, tenemos que añadir las siguientes tres columnas a la tabla de datos:

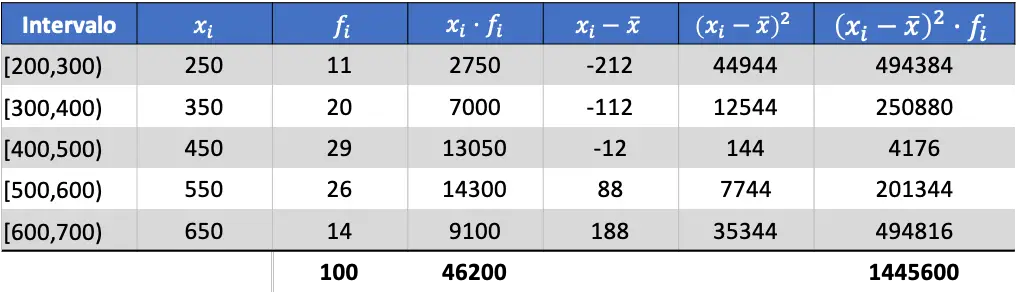
ejercicio resuelto de la desviacion estandar o desivacion tipica para datos agrupados

Entonces, la desviación estándar de los datos agrupados será el resultado de la raíz cuadrada del total de la última columna dividido por el número total de observaciones:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N\left(x_i-\overline{x}\right)^2\cdot f_i }{N}}=\sqrt{\frac{1445600}{100}}=120,23$

Desviación estándar (o típica) y varianza

La relación entre la desviación estándar (o desviación típica) y la varianza es que la desviación estándar es la raíz cuadrada de la varianza.

De manera que si conocemos el valor de la varianza de un conjunto de datos, podemos calcular fácilmente la desviación estándar sacando la raíz cuadrada. O al revés, si sabemos la desviación estándar podemos hallar la varianza elevando el valor al cuadrado.

$Var(X)=\sigma^2$

De hecho, la varianza se puede representar simplemente utilizando el símbolo de la desviación estándar elevado al cuadrado. Por lo tanto, el símbolo de la varianza poblacional es sigma al cuadrado (σ²) y el símbolo de la varianza muestral es una s al cuadrado (s²).

Además, tanto el concepto de desviación estándar y como el de la varianza tiene una interpretación similar, ya que ambos muestran la dispersión de una serie de datos estadísticos.

Propiedades de la desviación estándar (o desviación típica)

La desviación estándar tiene las siguientes propiedades:

La desviación estándar de una muestra de datos no puede ser negativa.

$\sigma \ge 0$

La desviación estándar será igual a cero si todos los datos son idénticos.

$\sigma =0$

Si se suma un término constante a todos los datos, el valor de la desviación estándar no varia.

$\sigma (X+k)=\sigma (X)$

Si se multiplican todos los datos por un número, la desviación estándar quedará multiplicada por el valor absoluto de dicho número.

$\sigma (k\cdot X)=|k|\cdot \sigma (X)$

La desviación estándar de la suma de dos variables aleatorias es igual a la raíz cuadrada de la suma de las varianzas de las variables más el doble de la covarianza entre las dos variables.

$\sigma(X+Y)=\sqrt{Var(X)+Var(Y)+2\cdot Cov(X,Y)}$

Si sabemos las desviaciones estándares de varias distribuciones (σ_i) y su número de datos (n_i), podemos calcular la desviación estándar total aplicando la siguiente fórmula:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle \sum_{i=1}^N n_i\cdot \sigma_i^2}{\displaystyle \sum_{i=1}^N n_i}}=\sqrt{\frac{\displaystyle n_1\cdot \sigma_1^2+n_2\cdot \sigma_2^2+\dots +n_N\cdot \sigma_N^2}{\displaystyle n_1+n_2+\dots+n_N}}$

6 comentarios en “Desviación estándar (o desviación típica)”

Arian
17/10/2022 a las 20:13

Gracias por la información. Sin embargo me queda la duda de saber a partir de CUÁNTO se considera baja o alta la desv. Estandar, qué parámetro se tiene en cuenta?. Vi dos problemas, en uno la SD era 6,8 y la consideraban baja, y en el otro problema, la DS era 5,5 y la consieraban alta. ¿Cuál es el criterio o con qué se compara para saber si es alta o baja?
GRACIAS POR SU RESPUESTA

Responder
1. Probabilidad y Estadística
  19/10/2022 a las 19:58
  
  Hola Arian,
  
  Buena pregunta. La respuesta es que el valor de la desviación estándar es alto o bajo dependiendo de los valores estadísticos.
  
  Por ejemplo, una desviación estándar de 5,2 es muy baja si trabajamos con valores entre 1500 y 1800. Sin embargo, una desviación estándar de 5,2 es muy alto si trabajamos con datos estadísticos cuyos valores varian entre 2 y 12.
monica
04/04/2023 a las 03:10

es decir que entonces tendriamos que sacar otra medida como el coeficiente de variacion para saber en que porcentaje los datos se encuentran cercanos a la media aritmetica ?

Responder
1. Probabilidad y Estadística
  11/04/2023 a las 23:03
  
  Efectivamente Monica, la desviación estándar solo indica la dispersión de un conjunto de datos. Mientras que el coeficiente de variación muestra la dispersión de un conjunto de datos respecto a su media aritmética.
  
  Puedes ver la explicación del coeficiente de variación y cómo se calcula en nuestra página web.
Rosa Valero
26/04/2023 a las 16:51

puedo obtener la desviación estándar relativa sin multiplicar por 100???

Responder
1. Probabilidad y Estadística
  28/04/2023 a las 23:40
  
  Buenas Rosa,
  
  En primer lugar, ten en cuenta que en este post hablamos sobre la desviación estándar, no sobre la desviación estándar relativa.
  
  En cuanto a la desviación estándar relativa, normalmente se multiplica por 100 porque se expresa en forma de porcentaje. Si lo deseas, puedes no multiplicar por cien, pero entonces el resultado no estará en forma de porcentaje.