En este artículo se explica qué es el rango semi-intercuartil en estadística. Así pues, encontrarás cómo sacar el rango semi-intercuartil, un ejercicio resuelto y, además, una calculadora online para calcular el rango semi-intercuartil de cualquier muestra de datos.
Índice
¿Qué es el rango semi-intercuartil?
El rango semi-intercuartil (o rango semi-intercuartílico) es la mitad de la diferencia entre el primer y el tercer cuartil. Por lo tanto, para calcular el rango semi-intercuartil se debe restar el tercer cuartil menos el primer cuartil y luego dividir entre dos.
El rango semi-intercuartil es una medida de dispersión que indica la variabilidad de los valores centrales. Así pues, cuanto mayor sea el rango semi-intercuartil de un conjunto de datos, significa que los valores del centro están más dispersos entre sí.
Una de las características del rango semi-intercuartil es que es un parámetro estadístico robusto, de manera que las observaciones atípicas no afectan al rango semi-intercuartil.
Así pues, el rango semi-intercuartil es una medida de dispersión similar al rango estadístico, ya que indica la variabilidad de un conjunto de datos haciendo la resta de dos valores cuartílicos. No obstante, el rango estadístico se calcula de manera ligeramente diferente.
Fórmula del rango semi-intercuartil
El rango semi-intercuartil es igual a la diferencia entre el tercer cuartil y el primer cuartil partido por dos. Por lo tanto, para calcular el rango semi-intercuartil primero se deben hallar el primer y el tercer cuartil, luego restarlos y, finalmente, dividir el resultado de la resta entre dos.
Así pues, la fórmula para calcular el rango semi-intercuartil es la siguiente:
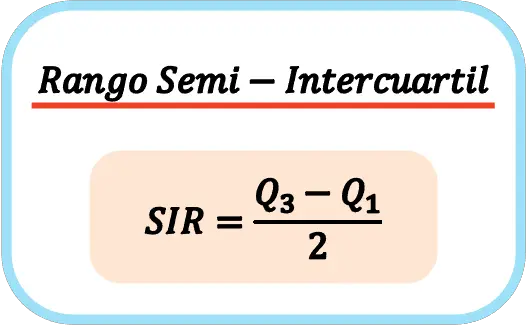
👉 Puedes usar la calculadora que hay más abajo para calcular el rango semi-intercuartil de cualquier conjunto de datos.
Generalmente, para representar al rango semi-intercuartil se suelen utilizar las siglas SIR (del inglés Semi Intquartile Range) como símbolo de esta medida estadística.
En definitiva, el rango semi-intercuartil es la mitad del rango intercuartil.
Ejemplo del cálculo del rango semi-intercuartil
Después de ver la definición de rango semi-intercuartil y cuál es su fórmula, a continuación se muestra un ejemplo resuelto para que quede claro cómo se calcula el rango semi-intercuartil.
- Se quiere analizar estadísticamente si es buena idea invertir en una empresa, para ello, se han recopilado los datos del precio de las acciones de dicha empresa durante los últimos 15 meses. En la siguiente tabla puedes ver los datos observados ordenados de menor a mayor. Calcula el rango semi-intercuartil de este conjunto de datos.

Tal y como se ha explicado en el apartado de arriba, para hallar el rango semi-intercuartil primero tenemos que determinar el primer y el tercer cuartil.
El primer cuartil es la mediana de la primera mitad de valores, que corresponde al valor 8,95 €/acción.
![]()
Por otro lado, el tercer cuartil es el valor intermedio de la segunda mitad de valores, esto es, 9,83 €/acción.
![]()
Una vez ya sabemos los valores del primer y el tercer cuartil, simplemente tenemos que aplicar la fórmula del rango semi-intercuartil para hallar su valor:
![]()
Calculadora del rango semi-intercuartil
Introduce un conjunto de datos estadísticos en la siguiente calculadora online para calcular su rango semi-intercuartil. Los datos deben separase por un espacio e introducirse usando el punto como separador decimal.
