En este artículo te explicamos qué es el rango en estadística y cómo se calcula. Encontrarás un ejercicio resuelto del rango de un conjunto de datos y, por último, te mostramos para qué sirve y cuándo se debe utilizar.
Índice
¿Qué es el rango en estadística?
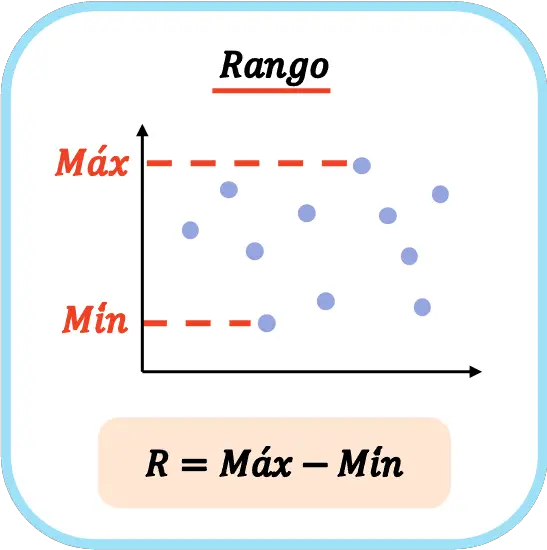
En estadística, el rango es una medida de dispersión que indica la diferencia entre el valor máximo y el valor mínimo de los datos de una muestra. Por lo tanto, para calcular el rango de una población o muestra estadística se debe restar el valor máximo menos el valor mínimo.
Por ejemplo, si el valor máximo de un conjunto de datos es 9 y el valor mínimo 2, el rango de esta muestra estadística es 7 (9-2=7).
El rango estadístico también se conoce como amplitud o recorrido de medida.
Así pues, el rango es una medida de dispersión junto con la varianza, la desviación típica (o desviación estándar), la desviación media y el coeficiente de variación.
Cómo calcular el rango en estadística
El rango de una muestra se calcula restando los valores extremos de los datos de la muestra estadística, es decir, el rango de una muestra es igual al valor máximo de todos los datos menos el valor mínimo.
Por lo tanto, la fórmula para calcular el rango estadístico de un conjunto de datos es la siguiente:
👉 Puedes utilizar la calculadora que hay más abajo para calcular el rango de cualquier conjunto de datos.
En estadística, se suele usar el símbolo de una R mayúscula para denotar el rango de una serie de datos.
De modo que el cálculo del rango de un conjunto de datos es bastante sencillo, ya que simplemente se debe determinar la diferencia entre los valores extremos. Lo único en lo que hay que prestar atención es en coger el dato máximo y el dato mínimo correctos y no olvidarse de ningún número.
Ejemplo del rango (estadística)
Vista la definición de rango en estadística, a continuación tienes un ejemplo resuelto para que veas cómo se saca el rango de un conjunto de datos.
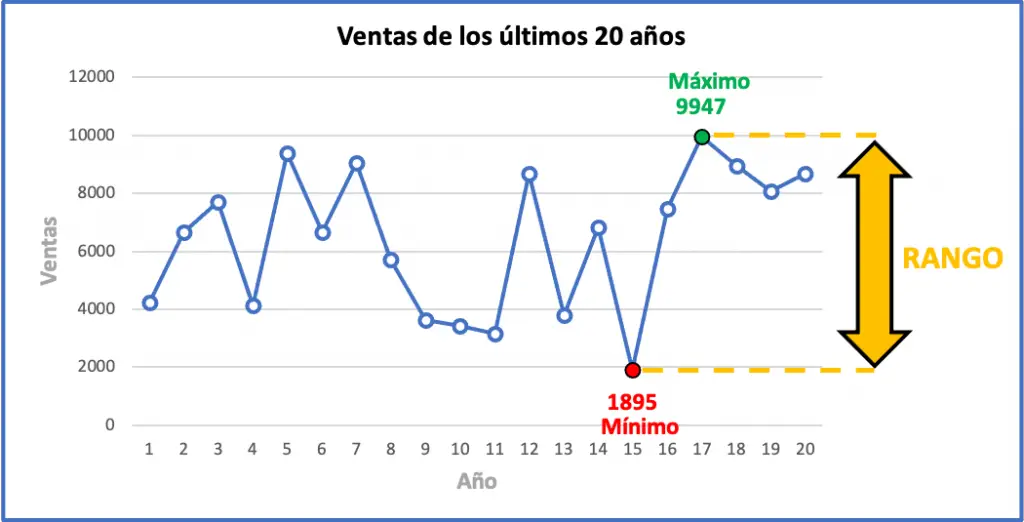
- En una empresa se quiere analizar estadísticamente las ventas conseguidas de su producto estrella durante los últimos veinte años. Para ello, te piden calcular varias métricas estadísticas entre ellas el rango. Si las ventas del producto son las mostradas en la siguiente tabla, ¿cuál es el rango de este conjunto de datos?

En este ejercicio tenemos 20 observaciones. En realidad, el número total de observaciones es indiferente para sacar el rango de una muestra, porque solo nos interesa el valor más grande y el valor más pequeño.
De modo que tenemos que usar la fórmula vista más arriba para hallar el rango de esta muestra estadística.
![]()
El valor máximo del intervalo es 9947 unidades vendidas y el valor mínimo es 1895. Por lo tanto, tenemos que restar estos dos valores para encontrar el rango del conjunto de datos:
![]()
Esto significa que la variación máxima que se ha producido de la ventas durante estos últimos años es de 8052 unidades. A continuación puedes ver representados gráficamente todos los datos del ejercicio junto con su rango estadístico, probablemente el gráfico te ayude a entender el significado de rango.
Calculadora del rango
Introduce un conjunto de datos estadísticos en la siguiente calculadora online para calcular su rango. Los datos deben separase por un espacio e introducirse usando el punto como separador decimal.
Para qué sirve el rango en estadística
Para acabar de entender el concepto de rango en estadística, vamos a ver para qué sirve y cómo se debe interpretar esta medida de dispersión.
En estadística, el rango muestra la diferencia entre el valor máximo y el valor mínimo de un conjunto de datos, por lo tanto, el rango es una medida que sirve para indicar la dispersión total de un conjunto de datos.
Cuando se sabe el valor del rango de una serie de datos, se conoce cuál es la máxima diferencia entre dos observaciones de ese conjunto, de modo que uno se puede hacer una idea de si los datos están muy dispersos o están muy juntos. En general, interesa que el rango sea el mínimo posible, ya que esto significa que hay poca dispersión y por tanto los cálculos serán más precisos.
Por ejemplo, el rango puede ser una medida que ayude a hacer la comparación entre dos muestras distintas, ya que permite tener una idea de las dispersiones de las muestras.
Sin embargo, hay que tener cuidado con la interpretación del rango estadístico, porque puede resultar engañoso. Podría ser que un conjunto de datos en realidad tuviera una dispersión muy pequeña, pero si hay un valor atípico (outlier) dentro de la muestra el rango será muy grande y por tanto no reflejará correctamente la dispersión de la muestra.
Además, no es lo mismo que una muestra cuyos valores son del orden de las decenas tenga un rango de 5, que una muestra con valores del orden de los millares tenga el mismo rango. Lógicamente, aunque los dos rangos son el mismo número, la primera muestra es mucho más dispersa que la segunda.
En conclusión, el rango es una medida estadística que es útil para analizar la dispersión de un conjunto de datos, pero para interpretar correctamente los datos también se deben calcular otras métricas.
