En este post se explica qué significa tipificar una distribución en estadística. Así pues, encontrarás la definición de tipificación, un ejemplo de cómo tipificar una variable y, además, podrás practicar con un ejercicio resuelto paso a paso.
Índice
¿Qué es la tipificación?
En estadística, la tipificación es un proceso en el cual se aplica una transformación lineal a una distribución para que su media y su desviación típica sean iguales a cero y uno respectivamente.
En concreto, la tipificación consiste en restar la media a la variable aleatoria y luego dividirla entre la desviación típica.
La tipificación también se puede llamar normalización o estandarización.
Fórmula de la tipificación
Para tipificar una variable se debe restar su media y luego dividir entre su desviación típica. Por lo tanto, la fórmula para tipificar una variable es la siguiente:
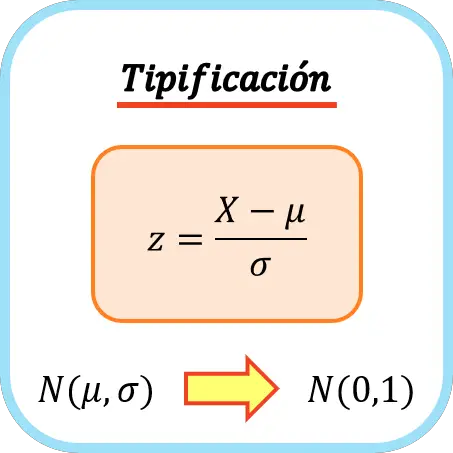
Donde ![]() es la media de la variable
es la media de la variable ![]() y
y ![]() su desviación típica (o desviación estándar).
su desviación típica (o desviación estándar).
Por lo tanto, la tipificación en realidad consiste en un cambio de variable, ya que se está aplicando una transformación lineal a la variable.
Ejemplo de tipificación
Vista la definición de tipificación y cuál es su fórmula, a continuación tienes un ejemplo resuelto para acabar de entender el concepto.
- Una variable aleatoria continua sigue una distribución normal de media 45 y desviación estándar 10, ¿cuál es la probabilidad de obtener un valor menor o igual que 60?
![]()
Para hallar la probabilidad de una distribución normal tenemos que usar su tabla característica pero, para ello, primero debemos llevar a cabo el proceso de tipificación. Así que restamos la media y dividimos entre la desviación estándar al valor de la probabilidad:

Una vez hemos tipificado, vamos a la tabla de probabilidades de la distribución normal para ver a qué probabilidad corresponde el valor de 1,5:

Tal y como se ve en la tabla de la tipificación de la distribución normal, el valor calculado en el paso anterior corresponde con la siguiente probabilidad:
![]()
Por lo tanto, la probabilidad de obtener un valor igual o más pequeño que 60 es del 93,32%.
Ejercicio resuelto de tipificación
Calcula las siguientes probabilidades de una distribución normal cuya media y desviación estándar son 120 y 50 respectivamente.
![]()
- La probabilidad de obtener un valor menor o igual que 208.
- La probabilidad de obtener un valor mayor que 137.
En ambos apartados del problema tenemos que tipificar la distribución normal para calcular las probabilidades.
Empezamos por el cálculo de la tipificación para la probabilidad de un valor menor o equivalente a 208:

Y ahora miramos en la tabla de arriba a qué probabilidad corresponde el valor 1,76:
![]()
En segundo lugar, vamos a calcular la probabilidad de conseguir un valor mayor que 137. Del mismo modo, empezamos tipificando la variable:

Sin embargo, la tabla adjuntada solo tiene las probabilidad acumuladas inferiores, por lo tanto, para poder usar la tabla antes tenemos que transformar la probabilidad:
![]()
Y, finalmente, tomamos de la tabla adjuntada arriba la probabilidad correspondiente al valor de Z calculado:
![]()
¿Para qué sirve la tipificación?
Para acabar de entender el significado de tipificación, vamos a ver para qué sirve y cuándo hay que tipificar una variable.
Principalmente, la tipificación sirve para comparar valores de distribuciones con media y varianza diferentes, asimismo, la tipificación también se utiliza para calcular una probabilidad.
Al tipificar dos valores de distribuciones con características distintas, podemos ver qué valor es más grande o más pequeño respecto a toda la distribución. O dicho con otras palabras, aplicando el proceso de tipificación podemos ver qué valor está más cerca o más lejos de la media de su distribución.
Además, tal y como se ha explicado más arriba, la tipificación también permite hacer el cálculo de probabilidades, ya que generalmente las tablas de probabilidad están en función de una distribución tipificada.
