En este post encontrarás qué significa una correlación positiva en estadística, ejemplos de variables con una correlación positiva y cuáles son las diferencias entre otros tipos de correlación.
Índice
¿Qué es la correlación positiva?
En estadística, la correlación positiva es un tipo de correlación entre dos variables diferentes. En concreto, una correlación positiva entre dos variables significa que si una variable aumenta de valor la otra variable también aumenta.
Para que una correlación entre dos variables se considere positiva, el valor del coeficiente de correlación debe estar entre 0 (no incluido) y 1 (incluido).
Ten en cuenta que la correlación positiva también se puede llamar correlación directa.
Ejemplo de correlación positiva
Vista la definición de correlación positiva, a continuación se muestra un ejemplo de dos variables con una correlación de este tipo.
- En la siguiente tabla de frecuencia, se han recogido como datos las notas de matemáticas y estadística de una muestra de 20 alumnos. Analiza la relación que hay entre las dos variables.
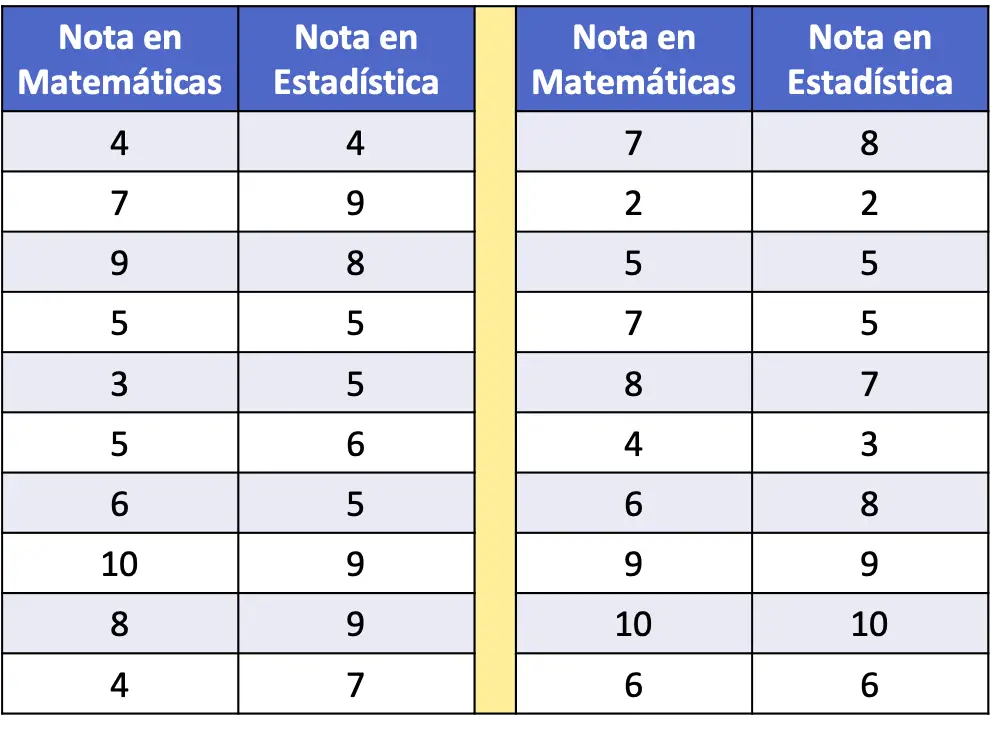
Antes de calcular el coeficiente de correlación, primero se recomienda representar el conjunto de datos estadísticos en un diagrama de dispersión para hacer una exploración previa.
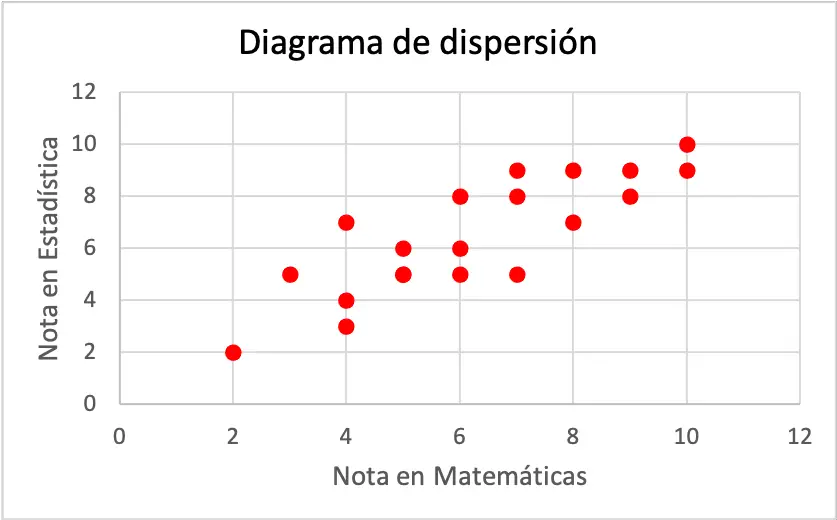
Tal y como se aprecia en el gráfico, parece que las dos variables tienen una correlación lineal positiva, ya que cuando aumenta la nota en matemáticas también aumenta la nota en estadística. Pero para determinar con certeza el tipo de correlación debemos calcular el coeficiente de correlación:
![]()
El valor del coeficiente de correlación de Pearson es mayor que 0 y muy próximo a 1, por lo tanto, la correlación entre las dos variables del estudio es efectivamente positiva.
Interpretación de la correlación positiva
Para acabar de entender el significado de correlación positiva en estadística, en este apartado veremos cómo interpretar el valor de una correlación positiva entre dos variables.
Cuanto mayor sea el valor del coeficiente de correlación, más correlacionadas positivamente están dos variables. Por lo tanto, cuando el valor del coeficiente de correlación es próximo a 1, significa que la correlación entre las dos variables es positiva y muy fuerte.
Por otro lado, cuando el valor del coeficiente de correlación es pequeño y está cerca del cero, quiere decir que la correlación entre las dos variables es positiva pero débil. Incluso si el coeficiente de correlación llega a ser cero o un valor negativo, implica que la correlación es nula o negativa respectivamente. Más abajo veremos las diferencias entre estos tres tipos de correlación.
Finalmente, cabe destacar que una correlación positiva no implica causalidad entre las variables. Es decir, si dos variables tienen una correlación positiva quiere decir que están relacionadas de manera lineal, pero no necesariamente una variable es la causa de la otra.
Siguiendo el ejemplo del apartado anterior, las notas en matemáticas y en estadística están correlacionadas positivamente, pero sacar una buena nota en matemáticas no te garantiza automáticamente obtener una buena nota en estadística, sino que se deben estudiar ambas asignaturas. En conclusión, la nota en matemáticas no es la causa de la nota en estadística, las dos variables simplemente están relacionadas.
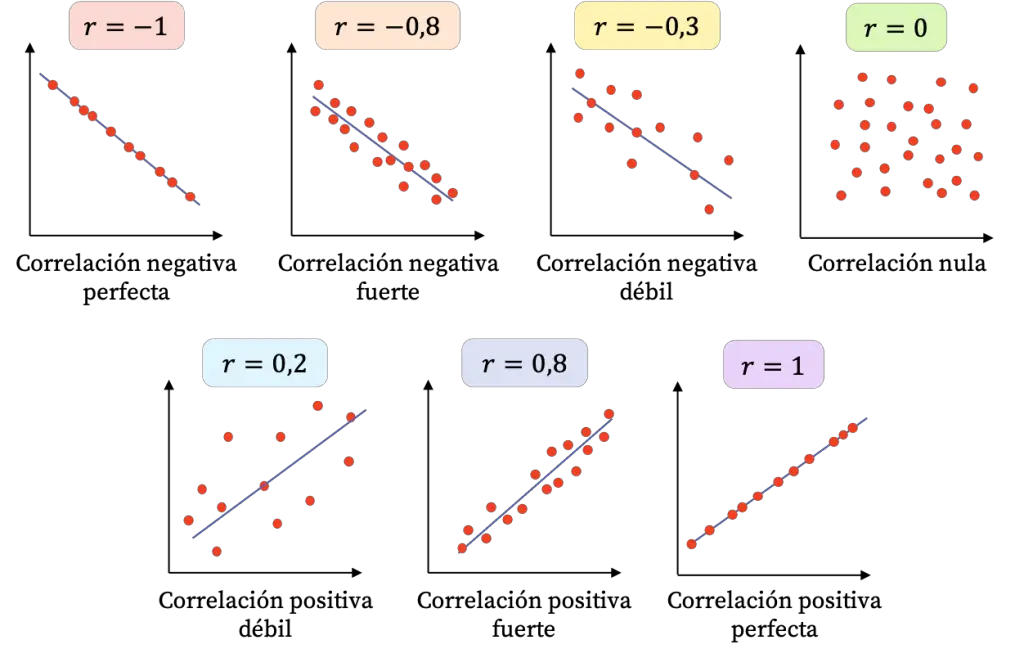
Correlación positiva, negativa y nula
Aparte de la correlación positiva, en estadística dos variables también pueden tener una correlación negativa o nula. Así pues, en este apartado veremos en qué se distinguen estos tres tipos de correlación.
- Correlación positiva: una variable aumenta cuando la otra también aumenta. El valor del coeficiente de correlación está entre 0 (no incluido) y 1 (incluido).
- Correlación negativa: cuando una variable aumenta la otra disminuye, y al revés, si una variable disminuye la otra aumenta. El valor del coeficiente de correlación está entre -1 (incluido) y 0 (no incluido).
- Correlación nula: no existe ninguna relación entre las dos variables. El coeficiente de correlación es igual a 0.
En las siguientes gráficas puedes ver representadas cada tipo de correlación:

Muy buena explicación, es muy importante conocer el ajuste de los puntos a la linea de regresión, junto con el coeficiente de relación, tanto gráficamente, como solo analizando el coeficiente.
¡Muchas gracias Ricardo!