En este artículo se explica el significado de la correlación entre dos variables, cómo calcular el coeficiente de correlación y los diferentes tipos de correlaciones que hay. Además, se muestra cómo se hace la interpretación del valor de la correlación entre dos variables.
Índice
¿Qué es la correlación?
La correlación es una medida estadística que indica el grado de relación entre dos variables. En concreto, la correlación lineal sirve para determinar cuánto de correlacionadas linealmente están dos variables distintas.
Dos variables están relacionadas cuando al variar los valores de una variable también cambian los valores de la otra variable. Por ejemplo, si al aumentar la variable A también aumenta la variable B, existe una correlación entre las variables A y B.
Tipos de correlación
Según cómo sea la relación que hay entre dos variables aleatorias, se distinguen los siguientes tipos de correlación lineal:
- Correlación directa (o correlación positiva): una variable aumenta cuando la otra también aumenta.
- Correlación inversa (o correlación negativa): cuando una variable aumenta la otra disminuye, y al revés, si una variable disminuye la otra aumenta.
- Correlación nula (sin correlación): no existe ninguna relación entre las dos variables.
Ten en cuenta que estos son los diferentes tipos de correlación lineal que hay, pero también puede ser que la relación matemática entre dos variables no se pueda representar con una recta, sino que se debe utilizar una función más compleja, como por ejemplo una parábola o un logaritmo. En tal caso sería una correlación no lineal.
Coeficiente de correlación
Vista la definición de correlación y cuáles son los diferentes tipos de correlación que hay, vamos a ver cómo se calcula este valor estadístico.
El coeficiente de correlación, también llamado coeficiente de correlación lineal o coeficiente de correlación de Pearson, es el valor de la correlación entre dos variables.
El coeficiente de correlación de dos variables estadísticas es igual al cociente entre la covarianza de las variables y la raíz cuadrada del producto de la varianza de cada variable. Por lo tanto, la fórmula para calcular el coeficiente de correlación es la siguiente:

Cuando se calcula el coeficiente de correlación sobre una población, el símbolo de la correlación es la letra griega ρ. Pero cuando se está calculando el coeficiente respecto a una muestra suele usarse como símbolo la letra r.
El valor del índice de correlación puede estar entre -1 y +1, ambos incluidos. Más abajo veremos cómo se interpreta el valor del coeficiente de correlación.
Puedes ver un ejemplo resuelto de cómo se calcula el coeficiente de correlación en el siguiente enlace:
Ten en cuenta que existen otros tipos de coeficientes de correlación, como por ejemplo el coeficiente de correlación de Spearman o el de Kendall. Pero sin duda el más habitual es el coeficiente de correlación de Pearson.
Interpretación de la correlación
El valor del coeficiente de correlación puede ir desde -1 hasta +1, ambos incluidos. Así pues, según el valor del coeficiente de correlación, significa que la relación entre las dos variables es de una forma u otra. A continuación se explica cómo interpretar el valor de la correlación:
- r=-1: las dos variables tienen una correlación perfecta negativa, por lo que se puede trazar una recta con pendiente negativa en la que se encuentren todos los puntos.
- -1<r<0: la correlación entre las dos variables es negativa, por lo tanto, cuando una variable aumenta la otra disminuye. Cuanto más cerca esté el valor de -1 significa que más relacionadas negativamente están las variables.
- r=0: la correlación entre las dos variables es muy débil, de hecho, la relación lineal entre ellas es nula. Esto no significa que las variables sean independientes, ya que podrían tener una relación no lineal.
- 0<r<1: la correlación entre las dos variables es positiva, cuanto más cerca esté el valor de +1 más fuerte es la relación entre las variables. En este caso, una variable tiende a incrementar su valor cuando la otra también aumenta.
- r=1: las dos variables tienen una correlación perfecta positiva, es decir, tienen una relación lineal positiva.
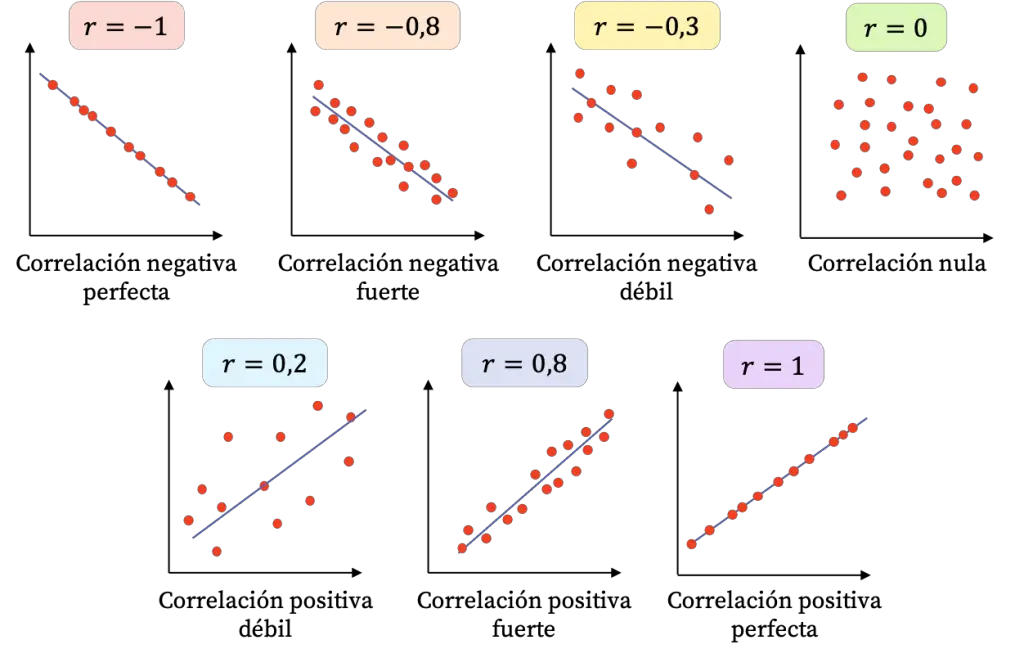
Como puedes ver en los gráficos de dispersión de arriba, cuanto más fuerte es la correlación entre dos variables más juntos están los puntos en el gráfico. Por otro lado, si los puntos están muy separados entre sí significa que la correlación es débil.
Ten presente que aunque haya correlación entre dos variables esto no significa que exista causalidad entre ellas, es decir, la correlación entre dos variables no significa que el cambio en una variable sea la causa del cambio en la otra variable.
Por ejemplo, si encontramos que hay una relación positiva entre la producción de dos hormonas diferentes del cuerpo, no tiene por qué ser que el incremento de una hormona cause el incremento de la otra hormona. Podría ser que el cuerpo produzca las dos hormonas porque necesita ambas para combatir una enfermedad y por tanto incremente el nivel de ambas simultáneamente, en este caso la causa sería la enfermedad. Para determinar si existe causalidad entre las dos hormonas se debería hacer una estudio más detallado.
Correlación y regresión
La correlación y la regresión son dos conceptos que suelen ir unidos, ya que ambos sirven para analizar la relación entre dos variables.
La correlación es una medida estadística que cuantifica la relación entre dos variables, en cambio, la regresión consiste en hacer un ecuación (si es una regresión lineal será una recta) que permita relacionar las dos variables.
De manera que la correlación simplemente proporciona un valor numérico a la relación entre variables, mientras que la regresión se puede utilizar para intentar predecir el valor de una variable a partir de la otra.
Normalmente, primero se analiza si las variables están correlacionadas calculando el coeficiente de correlación. Y si la correlación es significativa, entonces se procede a hacer una regresión del conjunto de datos.
Es habitual confundir el coeficiente de correlación con el valor de la pendiente de la recta obtenida en la regresión lineal, sin embargo, no son equivalentes.
Matriz de correlación
La matriz de correlación es una matriz que contiene en la posición i,j el coeficiente de correlación entre las variables i y j.
Por lo tanto, la matriz de correlación es una matriz cuadrada llena de unos en la diagonal principal y el elemento de la fila i y la columna j consiste en el valor del coeficiente de correlación entre la variable i y la variable j.
Así pues, la fórmula de la matriz de correlación es la siguiente:

Donde ![]() es el coeficiente de correlación entre las variables
es el coeficiente de correlación entre las variables ![]() y
y ![]()
La matriz de correlación resulta muy útil para resumir los resultados y comparar la correlación entre varias variables al mismo tiempo, ya que se puede ver rápidamente qué relaciones son más fuertes.
