En este post se explica qué es el coeficiente de correlación de Pearson (o coeficiente de correlación lineal) y para qué sirve. Encontrarás cómo calcular el coeficiente de correlación de Pearson junto con un ejercicio resuelto paso a paso. Además, podrás hallar el valor de coeficiente de correlación de Pearson de cualquier conjunto de datos con la calculadora online que hay al final.
Índice
¿Qué es el coeficiente de correlación de Pearson?
El coeficiente de correlación de Pearson, también llamado coeficiente de correlación lineal o simplemente coeficiente de correlación, es una medida estadística que indica la relación entre dos variables.
Para calcular el coeficiente de correlación de Pearson entre dos variables se debe dividir la covarianza de dichas variables por la raíz cuadrada del producto de sus varianzas.
De manera que el coeficiente de correlación de Pearson trata de cuantificar la dependencia lineal entre dos variables aleatorias cuantitativas. A priori, valorar numéricamente la correlación entre dos variables es complicado porque resulta difícil determinar qué pareja de variables está más correlacionada entre sí, así pues, el objetivo de coeficiente de correlación de Pearson es dar un valor a la relación entre variables para luego poder comparar entre ellas.
El valor del índice de correlación de Pearson está entre -1 y +1, ambos incluidos. Más abajo veremos cómo se interpreta el valor del coeficiente de correlación de Pearson.
Fórmula del coeficiente de correlación de Pearson
El coeficiente de correlación de Pearson de dos variables estadísticas es igual al cociente entre la covarianza de las variables y la raíz cuadrada del producto de la varianza de cada variable.
Por lo tanto, la fórmula para calcular el coeficiente de correlación de Pearson es la siguiente:
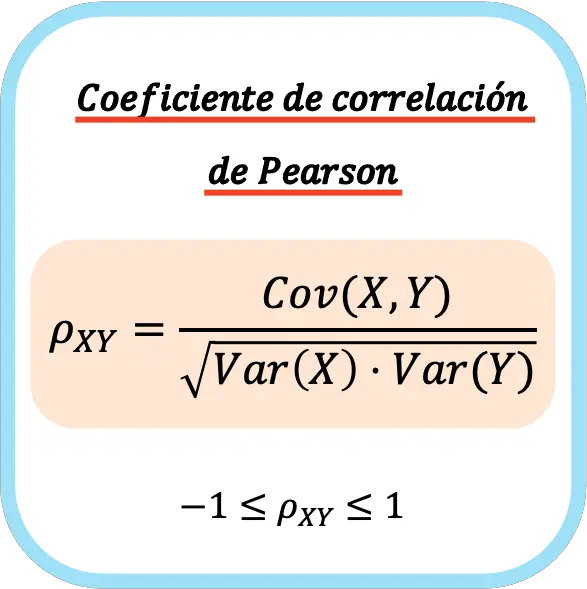
👉 Puedes usar la calculadora que hay más abajo para calcular el coeficiente de correlación de Pearson de cualquier conjunto de datos.
Cuando se calcula el coeficiente de correlación de Pearson sobre una población, se suele expresar mediante la letra griega ρ. Pero cuando se está calculando el coeficiente respecto a una muestra suele usarse como símbolo la letra r.
Ten en cuenta que para determinar el coeficiente de correlación de Pearson es imprescindible que sepas calcular la covarianza entre dos variables y la varianza de una variable, además, debes entender qué significan estas medidas estadísticas. Por lo que antes de seguir con la explicación se recomienda leer los siguientes dos artículos:
Ejemplo del cálculo del coeficiente de correlación de Pearson
Vista la definición del coeficiente de correlación de Pearson y su fórmula, a continuación tienes un ejemplo resuelto paso a paso para que así veas cómo se calcula.
- Calcula el coeficiente de correlación de Pearson entre las siguientes dos variables continuas:

Antes de hacer el cálculo del coeficiente de correlación de Pearson, representaremos el conjunto de datos en un gráfico de dispersión para analizar la relación entre las dos variables:
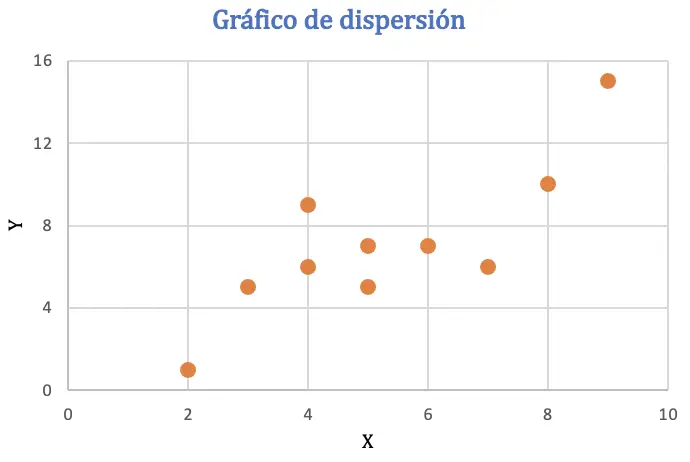
Del diagrama de dispersión se deduce que los datos pueden tener una tendencia positiva, o dicho de otra forma, cuando una variable aumenta de valor también aumenta la otra variable. Para comprobar la correlación vamos a hallar el coeficiente de Pearson.
Lo primero que debemos hacer es encontrar la media aritmética de cada variable por separado, que es equivalente a la suma total de los datos entre el número de observaciones.


Ahora que ya conocemos el promedio de cada variable, debemos añadir las siguientes columnas a la tabla de datos:

A partir de los datos calculados en la tabla, determinamos los valores de la covarianza y de las varianzas (si no recuerdas cómo se hacía tienes dos enlaces arriba donde se explica detalladamente):



Por último, solo nos queda aplicar la fórmula del coeficiente de correlación de Pearson para obtener su valor:

El coeficiente de correlación de Pearson tiene un valor muy próximo a 1, lo que significa que estas dos variables tienen una correlación positiva bastante fuerte.
Como has podido ver, para determinar el coeficiente de correlación de Pearson resulta muy útil usar programas como Excel para hacer los cálculos de las columnas de manera más rápida.
Calculadora del coeficiente de correlación de Pearson
Introduce un conjunto de datos estadísticos en la siguiente calculadora para calcular el coeficiente de correlación de Pearson entre dos variables. Debes separar las parejas de datos, de manera que en el primer recuadro solo haya los valores de una variable y en el segundo recuadro únicamente estén los valores de la segunda variable.
Los datos deben separase por un espacio e introducirse usando el punto como separador decimal.
Interpretar el coeficiente de correlación de Pearson
En este apartado veremos cómo interpretar el coeficiente de correlación de Pearson, ya que solo conociendo su valor no es suficiente, sino que tienes que saber analizar su significado.
De modo que la interpretación del coeficiente de correlación de Pearson depende de su valor:
- r=-1: las dos variables tienen una correlación perfecta negativa, por lo que se puede trazar una recta con pendiente negativa en la que se encuentren todos los puntos.
- -1<r<0: la correlación entre las dos variables es negativa, por lo tanto, cuando una variable aumenta la otra disminuye. Cuanto más cerca esté el valor de -1 significa que más relacionadas negativamente están las variables.
- r=0: la correlación entre las dos variables es muy débil, de hecho, la relación lineal entre ellas es nula. Esto no significa que las variables sean independientes, ya que podrían tener una relación no lineal.
- 0<r<1: la correlación entre las dos variables es positiva, cuanto más cerca esté el valor de +1 más fuerte es la relación entre las variables. En este caso, una variable tiende a incrementar su valor cuando la otra también aumenta.
- r=1: las dos variables tienen una correlación perfecta positiva, es decir, tienen una relación lineal positiva.

A modo de resumen, se presenta la siguiente tabla con las diferentes interpretaciones del coeficiente de correlación de Pearson:
| Valor | Interpretación |
|---|---|
| r=-1 | Correlación negativa perfecta. |
| -1<r<0 | Correlación negativa, cuanto más cerca de -1 más fuerte es la correlación. |
| r=0 | Correlación lineal nula. |
| 0<r<1 | Correlación positiva, cuanto más cerca de +1 más fuerte es la correlación. |
| r=1 | Correlación positiva perfecta. |
Ten en cuenta que aunque haya relación entre dos variables esto no significa que exista causalidad entre ellas, es decir, la correlación entre dos variables no significa que el cambio en una variable sea la causa del cambio en la otra variable.
Por ejemplo, si encontramos que hay una relación positiva entre la producción de dos hormonas diferentes del cuerpo, no tiene por qué ser que el incremento de una hormona cause el incremento de la otra hormona. Podría ser que el cuerpo produzca las dos hormonas porque necesita ambas para combatir una enfermedad y por tanto incremente el nivel de ambas simultáneamente, en este caso la causa sería la enfermedad. Para determinar si existe causalidad entre las dos hormonas se debería hacer una estudio más detallado.

muchas gracias por tu aporte, fue muy útil
¡Gracias Kevin!
Gracias me has ayudado mucho en la universidad
¡Me alegro por ti Melvin!
Excelente, he leído mucho tu página. Muchas gracias, me ayudo muchísimo.
¡Me alegro por ti Victor! ¡Muchísimas gracias!
Muchas gracias me fué muy util, bendiciones
¡Gracias María!
Excelente, gracias por tu aportación.
¡Gracias ti por comentar Roberto!
MUY BIEN EXPLICADO , GRACIAS
¡Muchas gracias Arcelia!
Buenos días,
Para quienes no tenemos dominio del proceso estadístico, en la interpretación de los resultados obtenido auxiliados de un software es muy didáctico, ya que nos permite explicar con propiedad los resultados de nuestra investigación.
Muchas gracias, saludos desde Huacho, Perú.
¡ Felicitaciones !. Muy importante y valioso apoyo, sobre todo lo pragmático que resulta entender este tema. Gracias, continuen así
No sabes cuanto me has salvado en mis clases
PD: Soy el profesor