En este artículo se explican cuáles son todos los tipos de correlación. Así pues, encontrarás varias maneras de clasificar la correlación: según si la relación es positiva o negativa, según el valor del coeficiente de correlación, según el número de variables…
Índice
¿Cuáles son los tipos de correlación lineal?
Para clasificar la relación que hay entre dos variables aleatorias, se distinguen los siguientes tipos de correlación lineal:
- Correlación directa (o correlación positiva): una variable aumenta cuando la otra también aumenta.
- Correlación inversa (o correlación negativa): cuando una variable aumenta la otra disminuye, y al revés, si una variable disminuye la otra aumenta.
- Correlación nula (sin correlación): no existe ninguna relación entre las dos variables.
Dependiendo de como sean los datos, la correlación directa también puede ser al mismo tiempo correlación directamente proporcional, aunque para ello el factor que relaciona las dos variables debe ser siempre igual. Por lo tanto, todas las relaciones directamente proporcionales son ejemplos de correlación directa, ya que las dos variables aumentan conjuntamente, pero no todas las relaciones directas son directamente proporcionales porque el grado de correlación puede variar según el tramo.
Del mismo modo, todas las variables que son inversamente proporcional también tienen una correlación negativa. Sin embargo, no todas las variables con correlación negativa son inversamente proporcionales, ya que para considerarse como tal la relación matemática entre ellas debe ser constante para todas las parejas de datos.
Tipos de correlación según el grado de correlación
Independientemente de si la correlación entre las dos variables es directa o inversa, la correlación también se puede clasificar en función de cuanto de fuerte o débil es la relación entre ambas variables.
- Correlación fuerte: las dos variables están muy relacionadas. Si se representan los datos en un gráfico de dispersión, los puntos están muy juntos entre sí. En consecuencia, resulta más fácil identificar la relación entre las variables.
- Correlación débil: existe una relación entre las dos variables, pero resulta difícil de identificar. Los puntos están muy separados en el gráfico de dispersión.
Para averiguar si la correlación entre dos variables es fuerte o débil se debe calcular el coeficiente de correlación. Cuanto mayor sea el valor absoluto del coeficiente de correlación más fuerte es la correlación entre las variables.
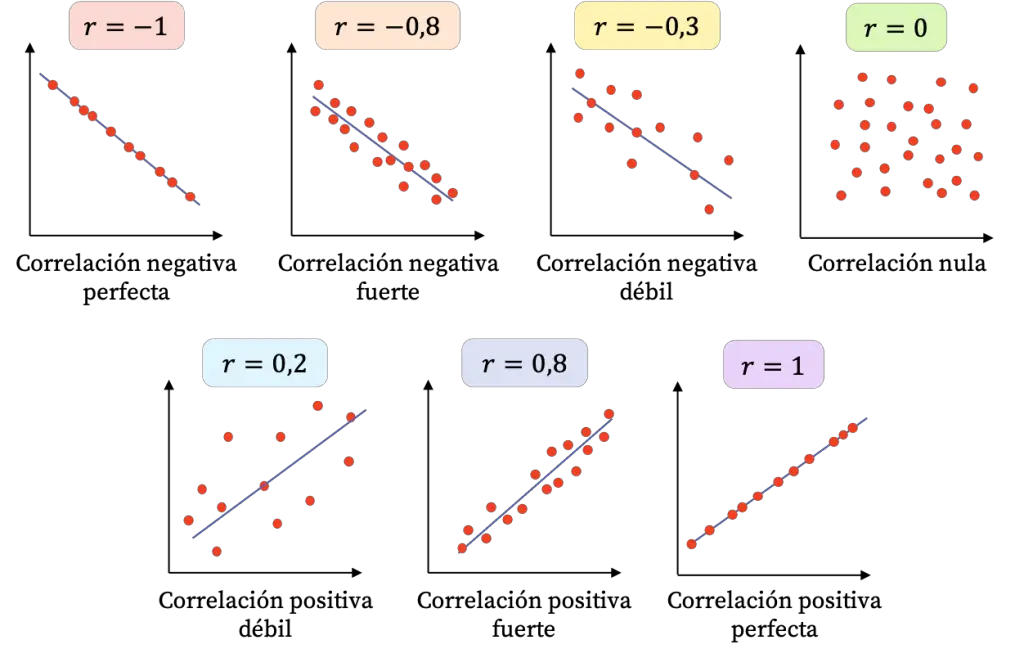
De modo que según el valor del coeficiente de correlación, la relación entre dos variables estadísticas diferentes se puede clasificar en los siguientes tipos:
| Valor del coeficiente de correlación | Tipo de correlación |
|---|---|
| -1 | Correlación negativa perfecta |
| -0,9 a -0,99 | Correlación negativa muy fuerte |
| -0,7 a -0,89 | Correlación negativa fuerte |
| -0,4 a -0,69 | Correlación negativa moderada |
| -0,2 a -0,39 | Correlación negativa débil |
| -0,01 a -0,19 | Correlación negativa muy débil |
| 0 | Correlación nula |
| 0,01 a 0,19 | Correlación positiva muy débil |
| 0,2 a 0,39 | Correlación positiva débil |
| 0,4 a 0,69 | Correlación positiva moderada |
| 0,7 a 0,89 | Correlación positiva fuerte |
| 0,9 a 0,99 | Correlación positiva muy fuerte |
| 1 | Correlación positiva perfecta |
Otros tipos de correlación
Acabamos de ver cuáles son los diferentes tipos de correlaciones lineales, sin embargo, debes tener en cuenta que hay más maneras de clasificar los tipos de correlación según otros criterios.
Si agrupamos los tipos de correlación según la naturaleza de la relación entre las variables, distinguimos entre:
- Correlación lineal: la relación entre las dos variables se puede representar mediante una línea recta.
- Correlación no lineal: la relación entre las dos variables no se puede representar con una recta, sino que se debe utilizar una función más compleja, como por ejemplo una parábola o un logaritmo.
Por otro lado, la correlación también se puede separar en diferentes grupos según el número de variables:
- Correlación simple: se estudia solamente la relación entre dos variables.
- Correlación múltiple: se estudia la relación entre más de dos variables.
- Correlación parcial: cuando la relación entre dos variables no afecta a las otras variables del conjunto de datos.
