En este artículo se explica qué es el valor crítico en estadística y cómo se debe interpretar en una prueba de hipótesis. Asimismo, podrás ver cómo se calcula el valor crítico junto con varios ejemplos resueltos.
Índice
¿Qué es el valor crítico?
El valor crítico es el punto en la distribución del estadístico de prueba que separa la región de rechazo de la hipótesis nula de su región de aceptación. Es decir, el valor crítico es aquel valor de la distribución de la prueba estadística que marca el límite de la región de rechazo (o región crítica).
Normalmente el valor crítico se representa con el símbolo Zα/2, ya que la distribución de referencia más habitual suele ser la distribución normal estándar.
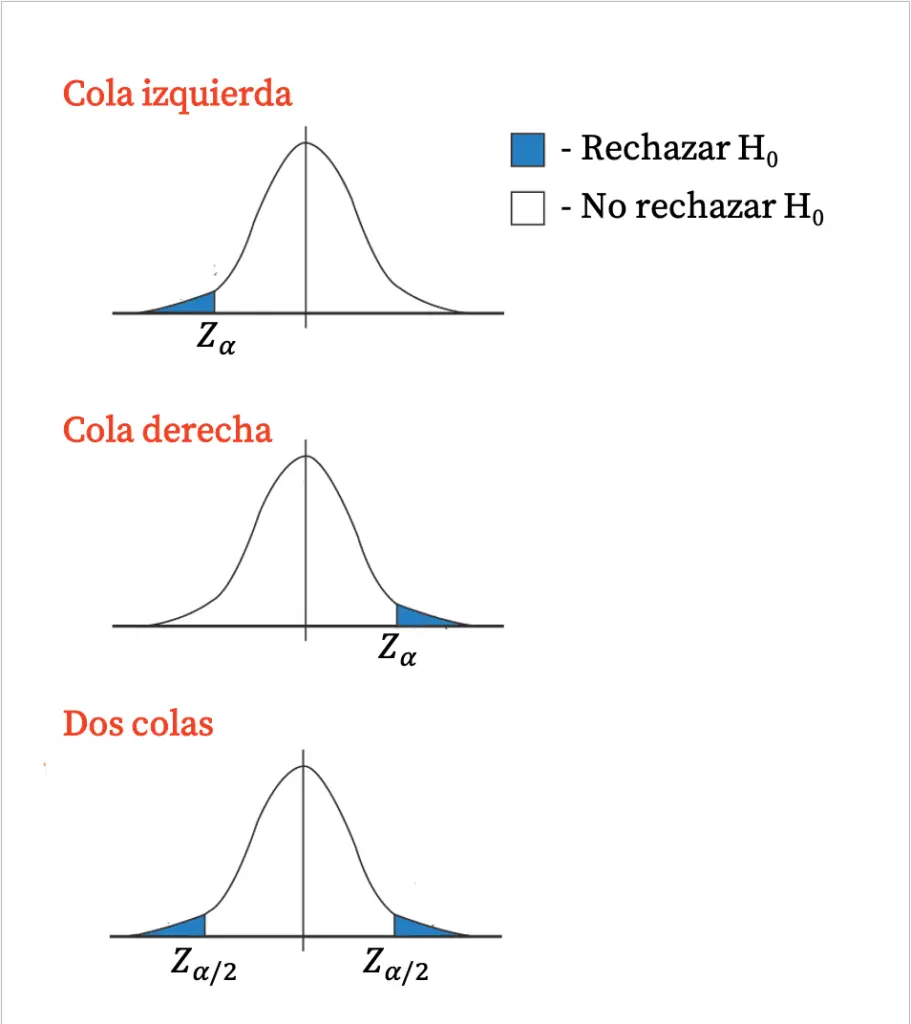
En general, las pruebas unilaterales tienen un valor crítico, ya que la región de rechazo es una sola cola de la distribución. Por otro lado, las pruebas bilaterales tienen dos valores críticos, porque la región de rechazo son las dos colas de la distribución.
En los intervalos de confianza, los valores críticos son los puntos de la distribución de referencia que marcan los límites del intervalo de confianza.
Cómo calcular el valor crítico
A continuación veremos cómo se calculan los valores críticos más usuales. Tanto el valor crítico de Z como el valor crítico de t se calculan para el intervalo de confianza para la media, la única diferencia es que el valor crítico de Z se calcula cuando se conoce la desviación típica de la población y, en cambio, el valor crítico de t se usa cuando solo se saben los datos de una muestra.
Valor crítico de Z
El valor crítico de Z se utiliza para determinar los límites del intervalo de confianza para la media. En concreto, solo se usa si conoce la desviación típica de la población.
Para calcular el valor crítico de Z se debe buscar en la tabla de la distribución normal estándar el valor correspondiente a la probabilidad de la mitad del nivel de significación.
Por ejemplo, si queremos determinar un intervalo de confianza para la media con un nivel de confianza del 95%, implica que el nivel de significación es del 5%. En consecuencia, tenemos que ver en la tabla de la distribución normal estándar qué valor corresponde a una probabilidad del 2,5%, ya que el intervalo de confianza para la media es bilateral.
![\begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-8427c95ebc909f8b082c47cd6ee62655_l3.svg "Rendered by QuickLaTeX.com")
A continuación puedes ver una tabla con los valores críticos de Z más utilizados:
| Nivel de confianza (1-α) | Nivel de significación (α) | Valor crítico (Z α/2) |
|---|---|---|
| 0,80 | 0,20 | 1,282 |
| 0,85 | 0,15 | 1,440 |
| 0,90 | 0,10 | 1,645 |
| 0,95 | 0,05 | 1,960 |
| 0,99 | 0,01 | 2,576 |
| 0,995 | 0,005 | 2,807 |
| 0,999 | 0,001 | 3,291 |
Valor crítico de t
El valor crítico de t se usa para hallar los límites del intervalo de confianza para la media cuando se desconoce la desviación típica de la población.
Para calcular el valor crítico de t se debe buscar en la tabla de la distribución t de Student el valor correspondiente a la probabilidad de la mitad del nivel de significación, teniendo en cuenta que los grados de libertad de la distribución t de Student son una unidad menos que el tamaño de la muestra.
Por ejemplo, si queremos hallar el intervalo de confianza con un nivel de confianza del 95% y el tamaño muestral es 8, tenemos que ir a la tabla de la distribución t de Student y ver qué valor corresponde a t0,025|7.
![\begin{array}{c}t_{\alpha/2| n-1}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 7}=2,365\end{array}](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-dcc22d369107cf7c6333d1bebafdaccd_l3.svg "Rendered by QuickLaTeX.com")
El valor crítico en el contraste de hipótesis
El valor crítico también se puede usar en el contraste de hipótesis para rechazar la hipótesis nula (y aceptar la hipótesis alternativa) o rechazar la hipótesis alternativa (y aceptar la hipótesis nula).
- Si el valor de la distribución del estadístico de prueba correspondiente al p-valor está dentro del intervalo marcado por los valores críticos, no se rechaza la hipótesis nula (se rechaza la hipótesis alternativa).
- Si el valor de la distribución del estadístico de prueba correspondiente al p-valor está fuera del intervalo marcado por los valores críticos, se rechaza la hipótesis nula (se acepta la hipótesis alternativa).
