En este post se explica qué es la distribución normal estándar y para qué sirve. También encontrarás las propiedades de la distribución normal estándar, la tabla con sus valores característicos y, además, un ejercicio resuelto.
Índice
¿Qué es la distribución normal estándar?
La distribución normal estándar, también llamada distribución normal unitaria, es el caso más simple de una distribución normal. En concreto, la distribución normal estándar es una distribución normal con valores de media y desviación estándar iguales a 0 y 1 respectivamente.
Por lo tanto, la distribución normal estándar se define como N(0,1), donde el primer parámetro es la media de la distribución y el segundo parámetro es su desviación estándar (o desviación típica).
![\displaystyle N(0,1) \ \color{orange}\bm{\longrightarrow}\color{black}\begin{cases} \mu=0\\[2ex]\sigma=1\end{cases}](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-ac4a0fb95aad0d42a73d0601500f7e40_l3.svg "Rendered by QuickLaTeX.com")
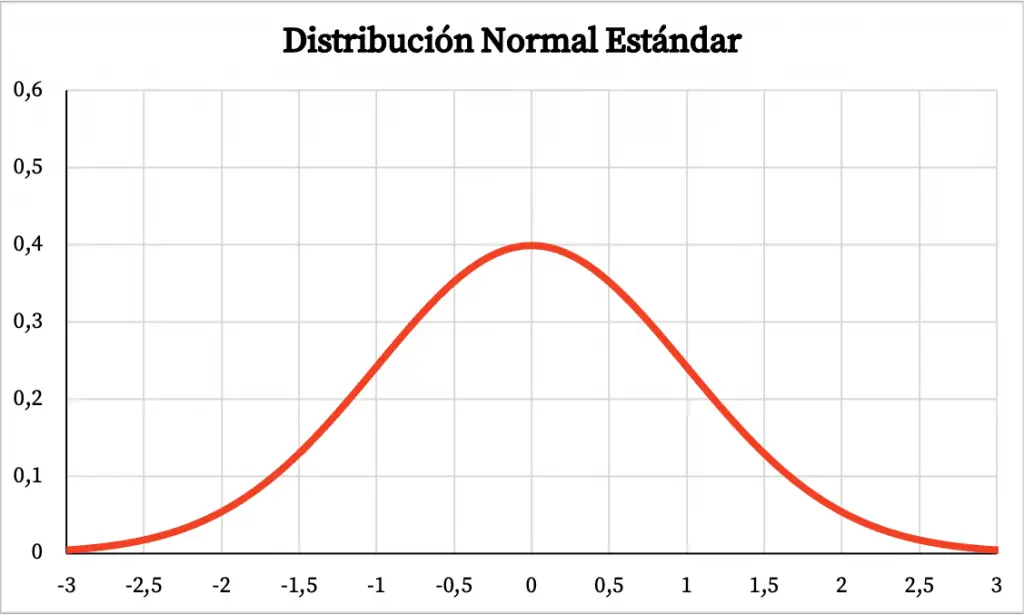
De modo que la gráfica de la distribución normal estándar es la siguiente:
Fórmula de la distribución normal estándar
Para transformar cualquier distribución normal en una distribución normal estándar, se debe restar la media de la distribución normal a todos sus valores y luego dividir por la desviación estándar de la distribución normal.
Así que la fórmula de la distribución normal estándar es la siguiente:
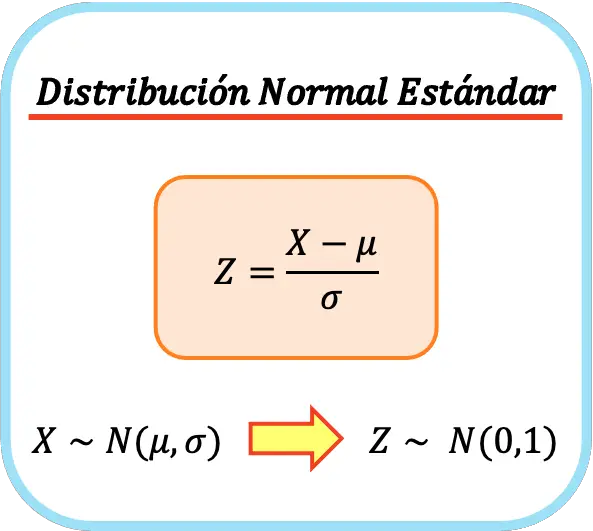
De este modo, la media aritmética y la desviación estándar de la nueva variable serán 0 y 1 respectivamente, por lo que obtendremos una distribución normal estándar. A este proceso también se le llama tipificación de una variable o normalización de una variable.
Tabla de la distribución normal estándar
La tabla de una distribución normal estándar es una tabla que contiene las probabilidades de que un valor observado esté por debajo de un valor dado de la distribución normal estándar.
Además, como la función de una distribución normal depende de su media y su desviación típica, la tabla de la distribución normal estándar también se usa, por extensión, para determinar las probabilidades de cualquier distribución normal. Para ello, se tipifica la distribución normal en una distribución normal estándar y luego se mira en la tabla qué probabilidad le corresponde.
Así pues, los valores de la tabla de la distribución normal estándar son los siguientes:
Ejemplo de la distribución normal estándar
Ahora que ya sabemos la definición de la distribución normal estándar y cuál es su fórmula, a continuación tienes un ejemplo resuelto para acabar de entender el concepto.
- Una variable aleatoria continua sigue una distribución normal de media 45 y desviación estándar 15, ¿cuál es la probabilidad de obtener un valor menor o igual que 58?
![N(45,15)\ \color{orange}\bm{\longrightarrow}\color{black}\ P[X\leq 58]= \ \color{orange}\bm{?}\color{black}](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-80eac52558b81ada09288188e1d7abd0_l3.svg "Rendered by QuickLaTeX.com")
Para hallar la probabilidad de una distribución normal tenemos que usar su tabla característica pero, para ello, primero debemos llevar a cabo el proceso de tipificación para obtener la distribución normal estándar. Así pues, utilizamos la fórmula de la distribución normal estándar:
De modo que restamos la media al valor de la probabilidad y luego dividimos entre la desviación estándar
![\displaystyle P[X\leq 58]=P\left[Z\leq\frac{58-45}{15}\right]=P[Z\leq 0,87]](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-7667761e6ccd9b721d47b6dba566315f_l3.svg "Rendered by QuickLaTeX.com")
Una vez hemos tipificado la variable, vamos a la tabla de probabilidades de la distribución normal estándar (vista más arriba) para ver a qué probabilidad corresponde el valor de 0,87:
![\displaystyle P[Z\leq 0,87]=0,8078](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-cf06df63ce799de5029282381c3ff7dc_l3.svg "Rendered by QuickLaTeX.com")
Por lo tanto, la probabilidad de obtener un valor igual o más pequeño que 58 es del 80,78%.
Características de la distribución normal estándar
La distribución normal estándar tiene las siguientes características:
- La distribución normal estándar es una distribución simétrica centrada en el 0.
- Al igual que una distribución normal, la gráfica de la distribución normal estándar tiene forma de campana y la mayor parte del área de la gráfica se encuentra alrededor de la media.
- Por lo tanto, la media, la moda y mediana de una distribución normal tienen el mismo valor, que es 0.
- La distribución normal estándar tiene un máximo en z=0.
- Asimismo, la distribución normal estándar tiene dos puntos de inflexión, en z=-1 y z=+1.
- A partir de la regla empírica, se sabe que el 68% de los valores se encuentran de una distribución normal estándar entre +1 y -1, el 95% de los valores entre +2 y -2 y el 99,7% de los valores entre +3 y -3.
