En este post se explica qué es el teorema de Bayes y para qué sirve en probabilidad y estadística. Así pues, encontrarás cuál es la fórmula del teorema de Bayes, ejemplos resueltos del teorema de Bayes y cuáles son las aplicaciones de este teorema.
Índice
¿Qué es el teorema de Bayes?
En la teoría de la probabilidad, el teorema de Bayes es una ley que sirve para calcular la probabilidad de un evento cuando se conoce información a priori sobre dicho suceso.
En concreto, el teorema de Bayes relaciona matemáticamente la probabilidad del evento A dado el evento B con la probabilidad de B dado A.
Por ejemplo, si se sabe de antemano la probabilidad de que una persona le duela la cabeza cuando tiene gripe, se puede determinar con el teorema de Bayes la probabilidad de que una persona tenga gripe cuando le duele la cabeza.
El teorema de Bayes tiene muchas aplicaciones, por ejemplo, se utiliza en medicina, en economía o en tecnología para calcular las probabilidades de algunos eventos que están condicionadas por otros eventos. Más abajo entraremos en detalle en las diferentes aplicaciones del teorema de Bayes.
El teorema de Bayes fue inventado por el matemático inglés Thomas Bayes (1702-1761), aunque fue publicado póstumamente en 1763.
Fórmula del teorema de Bayes
El teorema de Bayes dice que dado un espacio muestral formado por un conjunto de sucesos mutuamente excluyentes {A1, A2,…, Ai,…, An} cuyas probabilidades no son nulas y otro evento B, se puede relacionar matemáticamente la probabilidad condicional de Ai dado el evento B con la probabilidad condicional de B dado Ai.
Así pues, la fórmula del teorema de Bayes, también conocida como regla de Bayes, es la siguiente:

Donde:
 es la probabilidad condicional del evento Ai dado el evento B, denominada probabilidad a posteriori.
es la probabilidad condicional del evento Ai dado el evento B, denominada probabilidad a posteriori. es la probabilidad condicional del evento B dado el evento Ai.
es la probabilidad condicional del evento B dado el evento Ai. es la probabilidad de que ocurra el evento Ai, denominada probabilidad a priori.
es la probabilidad de que ocurra el evento Ai, denominada probabilidad a priori.
Fíjate que el denominador de la fórmula del teorema de Bayes corresponde a la probabilidad total del evento B.
Ejemplo del teorema de Bayes
Una vez hemos visto la definición del teorema de Bayes y cuál es su fórmula, vamos a ver un ejemplo resuelto de cómo se calcula una probabilidad con el teorema de Bayes para entender mejor el concepto.
- Una tienda de electrónica vende tres marcas de televisores: X, Y, Z. Se estima que el 20% de las ventas son televisores de la marca X, el 50% de la marca Y y el 30% de la marca Z. El 5% de los televisores de la marca X son defectuosos, el 3% de los televisores de la marca Y son defectuosos y el 4% de los televisores de la marca Z son defectuosos. Dado un televisor defectuoso, ¿cuál es la probabilidad de que sea de la marca de televisores Z?
El enunciado del ejercicio nos da las probabilidades de que un cliente compre cada marca de televisores:
- Evento A1: Un cliente compra un televisor de la marca X → P(A1)=0,20
- Evento A2: Un cliente compra un televisor de la marca Y → P(A2)=0,50
- Evento A3: Un cliente compra un televisor de la marca Z → P(A3)=0,30
Además, el enunciado también nos proporciona la probabilidad que un televisor sea defectuoso de cada marca:
Evento B: El televisor es defectuoso
- B|A1: Dado un televisor de la marca X, el televisor es defectuoso → P(B|A1)=0,05
- B|A2: Dado un televisor de la marca Y, el televisor es defectuoso → P(B|A2)=0,03
- B|A3: Dado un televisor de la marca Z, el televisor es defectuoso → P(B|A3)=0,04
De modo que el árbol de probabilidad de todos los eventos que nos interesan es el siguiente:
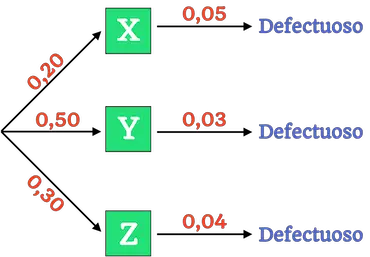
Entonces, para calcular la probabilidad de que dado un televisor defectuoso este sea de la marca Z, tenemos que usar la fórmula del teorema de Bayes:

Utilizando la terminología utilizada en este ejemplo, la fórmula de Bayes queda de la siguiente manera:

Por lo tanto, el cálculo de la probabilidad de que dado un televisor defectuoso este sea de la marca Z es el siguiente:
![Rendered by QuickLaTeX.com \begin{aligned}P(A_3|B)&=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}\\[2ex]&=\cfrac{0,04\cdot 0,30}{0,05\cdot 0,20+0,03\cdot 0,50+0,04\cdot 0,30}\\[2ex]&=0,32\end{aligned}](http://www.probabilidadyestadistica.net/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)
En conclusión, la probabilidad de que si un televisor es defectuoso este sea de la marca Z es del 32%.
Aplicaciones del teorema de Bayes
Las aplicaciones del teorema de Bayes son muchas, algunas de ellas son:
- Pruebas médicas: el teorema de Bayes se usa frecuentemente en medicina para determinar la probabilidad de acierto de las pruebas diagnósticas. Por ejemplo, en el caso de una prueba de detección del VIH, se puede utilizar el teorema para calcular la probabilidad de que una persona tenga realmente el virus dado un resultado positivo en la prueba.
- Análisis financiero: en finanzas se usa el teorema de Bayes para calcular la probabilidad de que ciertos eventos económicos, como un aumento o una bajada en el valor de las acciones, ocurran dado un conjunto de variables económicas.
- Estudio de mercado: el teorema de Bayes permite determinar, por ejemplo, la probabilidad de que una persona compre un producto cuando ha visto un anuncio de ese producto.
- Pronóstico del tiempo: los modelos meteorológicos también utilizan el teorema de Bayes para encontrar la probabilidad de que dada una predicción meteorológica en función de los datos observados esta se acabe cumpliendo. De esta forma se mejora la precisión de las previsiones climáticas.
- Seguridad informática: en ciberseguridad, el teorema de Bayes puede aplicarse para determinar la probabilidad de que una actividad sospechosa sea verdaderamente un ataque al sistema informático.
Ejercicios resueltos del teorema de Bayes
Ejercicio 1
Se estima que el 1% de la población tiene una cierta enfermedad. Una prueba para detectar esta enfermedad tiene una precisión del 95% para los casos positivos y del 90% para los casos negativos. Si una persona seleccionada al azar da positivo en la prueba, ¿cuál es la probabilidad de que realmente tenga la enfermedad?
El enunciado del ejercicio nos proporciona las siguientes probabilidades:
A1: La persona tiene la enfermedad → P(A1)=0,01
A2: La persona no tiene la enfermedad → P(A2)=0,99
B: La prueba da positivo
B|A1: La prueba da positivo cuando la persona tiene la enfermedad → P(B|A1)=0,95
B|A2: La prueba da positivo cuando la persona no tiene la enfermedad → P(B|A2)=1-0,90=0,10
Entonces, para calcular la probabilidad de que una persona seleccionada aleatoriamente tenga realmente la enfermedad cuando da positivo en la prueba se debe aplicar la regla de Bayes:


Así pues, sustituimos los valores en la fórmula y hacemos el cálculo de la probabilidad:
![Rendered by QuickLaTeX.com \begin{aligned}P(A_1|B)&=\cfrac{P(B|A_1)\cdot P(A_1)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)}\\[2ex]&=\cfrac{0,95\cdot 0,01}{0,95\cdot 0,01+0,10\cdot 0,99}\\[2ex]&=0,0876\end{aligned}](http://www.probabilidadyestadistica.net/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)
En definitiva, la probabilidad de que una persona escogida al azar dé positivo en la prueba y efectivamente tenga la enfermedad es del 8,76%.
Ejercicio 2
Se estima que la probabilidad de que una acción en la bolsa suba en un día es del 40%, que se mantenga estable es del 10% y que baje es del 50%. Además, se sabe que cuando el mercado sube hay un 90% de probabilidades de que un analista financiero lo prediga correctamente, cuando se mantiene estable la probabilidad de que predicción sea correcta es del 75% y cuando baja la probabilidad de predicción correcta es del 85%. Si un analista predice que el mercado bajará, ¿cuál es la probabilidad de que realmente baje?
En este caso, enunciado del ejercicio nos proporciona las siguientes probabilidades:
A1: El mercado sube en un día → P(A1)=0,40
A2: El mercado se mantiene estable en un día → P(A2)=0,10
A3: El mercado sube en un día → P(A3)=0,50
B: El analista predice que el mercado bajará
B|A1: El analista predice correctamente que el mercado subirá → P(B|A1)=0,90
B|A2: El analista predice correctamente que el mercado se mantiene estable → P(B|A2)=0,75
B|A3: El analista predice correctamente que el mercado bajará → P(B|A3)=0,85
Para determinar la probabilidad de que un analista haga la predicción de que el mercado bajará y sea correcta debemos emplear la fórmula del teorema de Bayes:


Sustituimos los valores de las probabilidades en la fórmula de Bayes y hacemos el cálculo de la probabilidad:
![Rendered by QuickLaTeX.com \begin{aligned}P(A_3|B)&=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}\\[2ex]&=\cfrac{0,85\cdot 0,50}{0,90\cdot 0,40+0,75\cdot 0,10+0,85\cdot 0,50}\\[2ex]&=0,4942\end{aligned}](http://www.probabilidadyestadistica.net/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)
Por lo tanto, la probabilidad de que un analista acierte cuando dice que el mercado de valores bajará es del 49,42%.

Gracias por el articulo.
Me resulto fácil de leer
¡Muchas gracias Juan!
me sirvió de muchisimo la explicación y los ejercicios de práctica; muchas gracias!!
¡Manuel me alegro de que te resulte útil la página! ¡Gracias!
Gracias por el artículo, lo forma de presentarlo hace que se entienda, comprenda y aprenda de manera fácil, estaba teniendo inconvenientes para interpretar el concepto central.
ME AYUDO MUCHISIMO A COMPRENDER GRACIASSSS
😊😊😊😊