En este artículo encontrarás cuál es la regla empírica en estadística y cuál es su fórmula. Además, podrás ver un ejercicio resuelto paso a paso sobre la regla empírica.
Índice
¿Qué es la regla empírica?
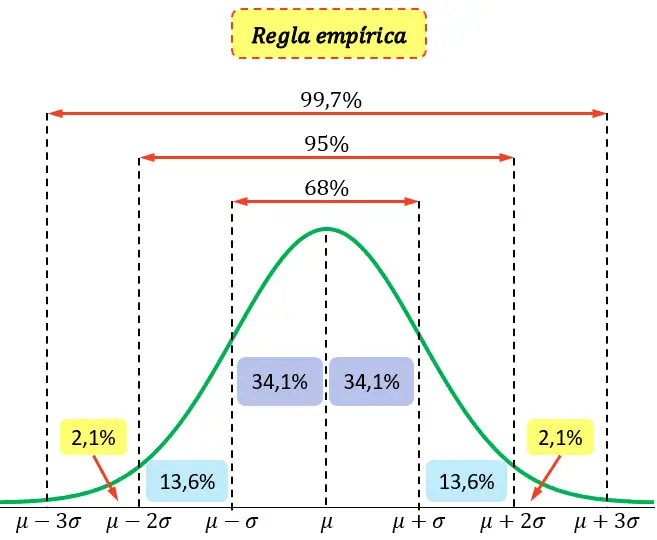
En estadística, la regla empírica, también llamada regla 68-95-99,7, es una regla que define el porcentaje de valores de una distribución normal que se encuentran a tres desviaciones estándar de la media.
Así pues, la regla empírica establece que:
- El 68% de los valores se encuentran a una desviación estándar de la media.
- El 95% de los valores se encuentran a dos desviaciones estándar de la media.
- El 99,7% de los valores se encuentran a tres desviaciones estándar de la media.
Fórmula de la regla empírica
La regla empírica también puede expresarse mediante las siguientes fórmulas:
Donde 
es una observación de una variable aleatoria regida por una distribución normal, 
es la media de la distribución y 
su desviación estándar.
Ejemplo de la regla empírica
Ahora que ya sabemos la definición de la regla empírica y cuál es su fórmula, vamos a ver un ejemplo resuelto sobre cómo calcular los valores representativos de la regla empírica de una distribución normal.
- Sabemos que el número de nacimientos anual en una localidad concreta sigue una distribución normal de media 10.000 y de desviación estándar 1000. Calcula los intervalos característicos de la regla empírica de esta distribución normal.
Tal y como se ha explicado arriba, las fórmulas para calcular los intervalos de la regla empírica son las siguientes:
Por lo tanto, sustituimos los datos del ejercicio en las fórmulas:
Y al hacer los cálculos, los resultados obtenidos son:
Así pues, se concluye que hay una probabilidad del 68,27% de que el número de nacimientos esté en el intervalo [9000,11000], un 95,45% de probabilidades que sea entre [8000,12000] y, por último, un 99,73% de probabilidades de que se encuentre entre [7000,13000].
Tabla de valores de la regla empírica
Aparte de los valores de 68, 95 y 99,7, también se pueden hallar más valores de probabilidades mediante la desviación estándar. A continuación puedes ver una tabla con las probabilidades para una distribución normal:
| Rango | Probabilidad |
|---|---|
| μ ± 0.5σ | 0,382924922548026 |
| μ ± 1σ | 0,682689492137086 |
| μ ± 1.5σ | 0,866385597462284 |
| μ ± 2σ | 0,954499736103642 |
| μ ± 2.5σ | 0,987580669348448 |
| μ ± 3σ | 0,997300203936740 |
| μ ± 3.5σ | 0,999534741841929 |
| μ ± 4σ | 0,999936657516334 |
| μ ± 4.5σ | 0,999993204653751 |
| μ ± 5σ | 0,999999426696856 |
| μ ± 5.5σ | 0,999999962020875 |
| μ ± 6σ | 0,999999998026825 |
| μ ± 6.5σ | 0,999999999919680 |
| μ ± 7σ | 0,999999999997440 |
Todos estos valores numéricos de la tabla provienen de la función de probabilidad acumulada de la distribución normal.
