En este artículo se explica cómo calcular la desviación estándar relativa. Encontrarás qué es la desviación estándar relativa, cuál es su fórmula, y un ejercicio resuelto paso a paso.
Índice
¿Qué es la desviación estándar relativa?
La desviación estándar relativa es una medida estadística que indica la dispersión de un conjunto de datos respecto a su media. La desviación estándar relativa se calcula dividiendo la desviación estándar de los datos entre su promedio.
La desviación estándar relativa se expresa en forma de porcentaje y su valor siempre será positivo.
La interpretación de la desviación estándar relativa sirve para mostrar la dispersión de una muestra de datos. Cuanto mayor sea el valor de la desviación estándar relativa, significa que más dispersos son los datos. Y cuanto menor sea la desviación estándar relativa, quiere decir que más cerca están los datos de su media.
En general, se usan las siglas RSD como símbolo de la desviación estándar relativa (del inglés Relative Standard Deviation).
Fórmula de la desviación estándar relativa
La desviación estándar relativa es igual a la desviación estándar entre la media multiplicado por 100. Por lo tanto, para calcular la desviación estándar relativa primero se debe determinar la desviación estándar y la media aritmética, luego dividir las dos métricas estadísticas y, por último, multiplicar por 100.
Es decir, la fórmula de la desviación estándar relativa es la siguiente:
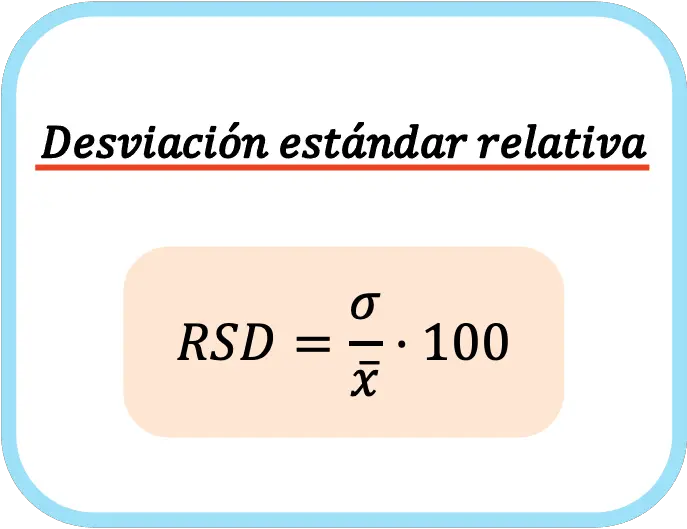
En el cálculo de la desviación estándar relativa se multiplica por cien para expresar el valor en forma de porcentaje.
Ejemplo del cálculo de la desviación estándar relativa
Después de ver la definición de la desviación estándar relativa y su fórmula, a continuación puedes ver un ejemplo resuelto de cómo se calcula la desviación estándar relativa.
- Calcula la desviación estándar relativa del siguiente conjunto de datos estadísticos:
4, 1, 3, 9, 12, 2, 5, 8, 3, 6
Primero de todo, tenemos que encontrar la desviación estándar de los datos:
![]()
En segundo lugar, calculamos la media aritmética de los datos:
![]()
Una vez sabemos la desviación estándar y la media aritmética de la serie de datos, utilizamos la fórmula de la desviación estándar relativa.
![]()
Y, finalmente, sustituimos los valores calculados en la fórmula y hacemos el cálculo de la desviación estándar relativa:
![]()
