▷ Contraste de hipótesis

En este post se explica qué es un contraste de hipótesis en estadística. Así pues, encontrarás cómo se hace un contraste de hipótesis, los diferentes tipos de contrastes de hipótesis y los posibles errores que se pueden cometer al realizar un contraste de hipótesis.

Índice

¿Qué es un contraste de hipótesis?

Un contraste de hipótesis es un procedimiento que sirve para rechazar o no una hipótesis estadística. En un contraste de hipótesis se juzga si el valor de un parámetro poblacional es compatible con lo observado en una muestra de dicha población.

Es decir, en un contraste de hipótesis se analiza una muestra estadística y, a partir de los resultados obtenidos, se determina si se rechaza o se acepta una hipótesis establecida previamente.

Ten en cuenta que, en general, de un contraste de hipótesis no se puede deducir con total certeza que una hipótesis es falsa o verdadera, sino que simplemente se rechaza o no se rechaza una hipótesis según los resultados obtenidos. De manera que en los contrastes de hipótesis siempre se puede cometer un error aunque exista evidencia estadística que indique que la decisión tomada sea la más probable.

En estadística, un contraste de hipótesis también se conoce como test de hipótesis, prueba de hipótesis o prueba de significación.

La teoría de los contrastes de hipótesis fue establecida por el estadístico inglés Ronald Fisher y se continuó elaborando posteriormente por Jerzy Neyman y Egon Pearson.

Hipótesis nula e hipótesis alternativa

Un contraste de hipótesis está formado por dos tipos de hipótesis estadísticas:

Hipótesis nula (H₀): es la hipótesis que sostiene que la suposición inicial que se tiene respecto a un parámetro poblacional es falsa. Por lo tanto, la hipótesis nula es aquella hipótesis que se pretende rechazar.

Hipótesis alternativa (H₁): es la hipótesis de la investigación que se pretende probar que es cierta. Es decir, la hipótesis alternativa es una suposición previa que tiene el investigador y para intentar demostrar que es verdadera llevará a cabo el contraste de hipótesis.

En la práctica, la hipótesis alternativa se formula antes que la hipótesis nula, ya que es la suposición que se pretende corroborar analizando estadísticamente una muestra de datos. Luego se formula la hipótesis nula simplemente contradiciendo la hipótesis alternativa.

Tipos de contrastes de hipótesis

Los contrastes de hipótesis se pueden clasificar en dos tipos distintos:

Contraste de hipótesis bilateral (o contraste de hipótesis de dos colas): la hipótesis alternativa del contraste de hipótesis afirma que el parámetro poblacional es «diferente a» un valor concreto.
Contraste de hipótesis unilateral (o contraste de hipótesis de una cola): la hipótesis alternativa del contraste de hipótesis afirma que el parámetro poblacional es «mayor que» (cola derecha) o «menor que» (cola izquierda) un valor concreto.

Contraste de hipótesis bilateral

$\begin{cases}H_0: \mu=\mu_0\\[2ex]H_1:\mu\neq\mu_0\end{cases}$

Contraste de hipótesis unilateral (cola derecha)

$\begin{cases}H_0: \mu\leq \mu_0\\[2ex]H_1:\mu>\mu_0\end{cases}$

Contraste de hipótesis unilateral (cola izquierda)

$\begin{cases}H_0: \mu\geq\mu_0\\[2ex]H_1:\mu<\mu_0\end{cases}$

Región de rechazo y región de aceptación de un contraste de hipótesis

Como veremos detalladamente más abajo, el contraste de hipótesis consiste en calcular un valor característico de cada tipo de prueba de hipótesis, dicho valor se llama estadístico del contraste de hipótesis. Así pues, una vez se ha calculado el estadístico del contraste, se debe observar en cuál de la siguientes dos regiones cae para llegar a una conclusión:

Región de rechazo (o región crítica): es la zona de la gráfica de la distribución de referencia del contraste de hipótesis que implica rechazar la hipótesis nula (y aceptar la hipótesis alternativa).
Región de aceptación: es la zona de la gráfica de la distribución de referencia del contraste de hipótesis que implica aceptar la hipótesis nula (y rechazar la hipótesis alternativa).

En definitiva, si el estadístico del contraste cae en la región de rechazo, se rechaza la hipótesis nula y se acepta la hipótesis alternativa. Por el contrario, si el estadístico del contraste cae en la región de aceptación, se acepta la hipótesis nula y se rechaza la hipótesis alternativa.

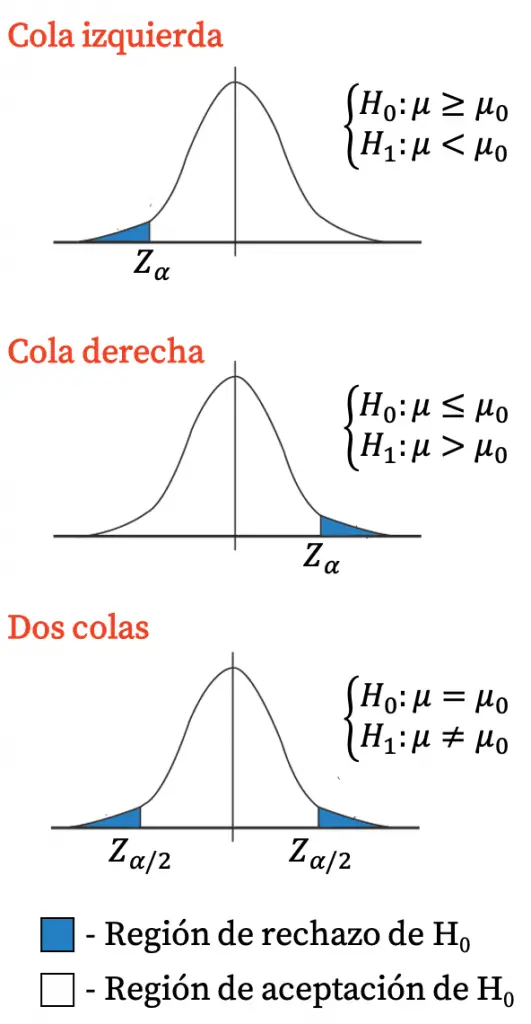
Los valores que establecen los límites de la región de rechazo y de la región de aceptación se llaman valores críticos, asimismo, el intervalo de valores que define la región de rechazo se llama intervalo de confianza. Y ambos valores dependen del nivel de significación escogido.

➤ Ver: Nivel de significación alfa

Por otro lado, la decisión de rechazar o aceptar la hipótesis nula también se puede realizar comparando el p-valor (o valor p) obtenido del contraste de hipótesis con el nivel de significación elegido.

➤ Ver: ¿Qué es el p-valor?

Cómo hacer un contraste de hipótesis

Para hacer un contraste de hipótesis se deben seguir los siguientes pasos:

Plantear la hipótesis nula y la hipótesis alternativa del contraste de hipótesis.
Establecer el nivel de significación alfa (α) deseado.

Calcular el estadístico del contraste de hipótesis.
Determinar los valores críticos del contraste de hipótesis para averiguar la región de rechazo y la región de aceptación del contraste de hipótesis.
Observar si el estadístico del contraste de hipótesis cae en la región de rechazo o en la región de aceptación.

Si el estadístico cae en la región de rechazo, se rechaza la hipótesis nula (y se acepta la hipótesis alternativa). Pero si el estadístico cae en la región de aceptación, se acepta la hipótesis nula (y se rechaza la hipótesis alternativa).

➤ Ver: Contraste de hipótesis para la media
➤ Ver: Contraste de hipótesis para la proporción
➤ Ver: Contraste de hipótesis para la varianza

Errores de un contraste de hipótesis

En un contraste de hipótesis, al rechazar una hipótesis y aceptar la otra hipótesis del contraste, se puede cometer uno de los siguientes dos errores:

Error tipo I: es el error cometido al rechazar la hipótesis nula cuando en realidad es verdadera.
Error tipo II: es el error cometido al aceptar la hipótesis nula cuando en realidad es falsa.

Por otro lado, la probabilidad de cometer cada tipo de error se llama de la siguiente manera:

Probabilidad alfa (α): es la probabilidad de cometer el error de tipo I.
Probabilidad beta (β): es la probabilidad de cometer el error de tipo II.

Asimismo, la potencia del contraste de hipótesis se define como la probabilidad de rechazar la hipótesis nula (H₀) cuando esta es falsa, o dicho de otra forma, es la probabilidad de escoger la hipótesis alternativa (H₁) cuando esta es cierta. Por lo tanto, la potencia del contraste de hipótesis es igual a 1-β.

Estadísticos de contrastes de hipótesis

El estadístico de un contraste de hipótesis es el valor de la distribución de referencia del contraste de hipótesis que sirve para determinar si se rechaza o no la hipótesis nula. Si el estadístico del contraste cae en la región de rechazo se rechaza la hipótesis nula (y se acepta la hipótesis alternativa), por otro lado, si el estadístico del contraste cae en la región de aceptación se acepta la hipótesis nula (y se rechaza la hipótesis alternativa).

El cálculo del estadístico del contraste de hipótesis depende del tipo de contraste, así pues, a continuación se muestra la fórmula para calcular el estadístico de cada tipo de contraste de hipótesis.

Contraste de hipótesis para la media

La fórmula del estadístico del contraste de hipótesis para la media con varianza conocida es la siguiente:

$\displaystyle Z=\frac{\overline{x}-\mu}{\displaystyle \frac{\sigma}{\sqrt{n}}}$

Donde:

$Z$ es el estadístico del contraste de hipótesis para la media.
$\overline{x}$ es la media muestral.
$\mu$ es el valor de la media propuesto.

$\sigma$ es la desviación estándar de la población.
$n$ es el tamaño de la muestra.

Una vez se ha calculado el estadístico del contraste de hipótesis de hipótesis para la media, se debe interpretar el resultado para rechazar o no la hipótesis nula:

Si el contraste de hipótesis para la media es de dos colas, se rechaza la hipótesis nula si el valor absoluto del estadístico es mayor que el valor crítico Z_α/2.
Si el contraste de hipótesis para la media corresponde a la cola derecha, se rechaza la hipótesis nula si el estadístico es mayor que el valor crítico Z_α.
Si del contraste de hipótesis para la media corresponde a la cola izquierda, se rechaza la hipótesis nula si el estadístico es menor que el valor crítico -Z_α.

$\begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |Z|>Z_{\alpha/2} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z>Z_{\alpha} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z<-Z_{\alpha} \text{ se rechaza } H_0\end{array}$

En este caso, los valores críticos se obtienen de la tabla de la distribución normal estandarizada.

Por otro lado, la fórmula del estadístico del contraste de hipótesis para la media con varianza desconocida es la siguiente:

$\displaystyle t=\frac{\overline{x}-\mu}{\displaystyle \frac{s}{\sqrt{n}}}$

Donde:

$t$ es el estadístico del contraste de hipótesis para la media, el cual está definido por una distribución t Student.

$\overline{x}$ es la media de la muestra.
$\mu$ es el valor de la media propuesto.
$s$ es la desviación estándar de la muestra.

$n$ es el tamaño de la muestra.

Igual que antes, se debe interpretar el resultado calculado del estadístico del contraste con el valor crítico para rechazar o no la hipótesis nula:

Si el contraste de hipótesis para la media es de dos colas, se rechaza la hipótesis nula si el valor absoluto del estadístico es mayor que el valor crítico t_α/2|n-1.

Si el contraste de hipótesis para la media corresponde a la cola derecha, se rechaza la hipótesis nula si el estadístico es mayor que el valor crítico t_α|n-1.
Si el contraste de hipótesis para la media corresponde a la cola izquierda, se rechaza la hipótesis nula si el estadístico es menor que el valor crítico -t_α|n-1.

$\begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |t|>t_{\alpha/2|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t>t_{\alpha|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t<-t_{\alpha|n-1} \text{ se rechaza } H_0\end{array}$

Cuando la varianza es desconocida, los valores críticos del contraste se obtienen de la tabla de la distribución t Student.

Contraste de hipótesis para la proporción

La fórmula del estadístico del contraste de hipótesis para la proporción es la siguiente:

$\displaystyle Z=\frac{\widehat{p}-p}{\displaystyle\sqrt{\frac{p(1-p)}{n}}}$

Donde:

$Z$ es el estadístico de la prueba de hipótesis para la proporción.
$\widehat{p}$ es la proporción muestral.

$p$ es el valor de la proporción propuesto.
$n$ es el tamaño muestral.
$\displaystyle\sqrt{\frac{p(1-p)}{n}}$ es la desviación estándar de la proporción.

Ten presente que no basta con calcular el estadístico de la prueba de hipótesis para la proporción, sino que luego se debe interpretar el resultado:

Si el contraste de hipótesis para la proporción es de dos colas, se rechaza la hipótesis nula si el valor absoluto del estadístico es mayor que el valor crítico Z_α/2.
Si el contraste de hipótesis para la proporción corresponde a la cola derecha, se rechaza la hipótesis nula si el estadístico es mayor que el valor crítico Z_α.

Si el contraste de hipótesis para la proporción corresponde a la cola izquierda, se rechaza la hipótesis nula si el estadístico es menor que el valor crítico -Z_α.

$\begin{array}{l}H_1: p\neq p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |Z|>Z_{\alpha/2} \text{ se rechaza } H_0\\[3ex]H_1: p> p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z>Z_{\alpha} \text{ se rechaza } H_0\\[3ex]H_1: p< p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z<-Z_{\alpha} \text{ se rechaza } H_0\end{array}$

Recuerda que los valores críticos se pueden obtener fácilmente de la tabla de la distribución normal estándar.

Contraste de hipótesis para la varianza

La fórmula para calcular el estadístico del contraste de hipótesis para la varianza es la siguiente:

$\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

Donde:

$\chi^2$ es el estadístico del contraste de hipótesis para la varianza, el cual tiene una distribución chi-cuadrado.
$n$ es el tamaño muestral.
$s^2$ es la varianza de la muestra.

$\sigma^2$ es la varianza de la población propuesta.

Para interpretar el resultado del estadístico, se debe comparar el valor obtenido con el valor crítico de la prueba.

Si el contraste de hipótesis para la varianza es de dos colas, se rechaza la hipótesis nula si el estadístico es mayor que el valor crítico $\chi_{1-\alpha/2|n-1}^2$ o si el valor crítico es menor que $\chi_{\alpha/2|n-1}$ .

Si el contraste de hipótesis para la varianza corresponde a la cola derecha, se rechaza la hipótesis nula si el estadístico es mayor que el valor crítico $\chi_{1-\alpha|n-1}^2$ .
Si el contraste de hipótesis para la varianza corresponde a la cola izquierda, se rechaza la hipótesis nula si el estadístico es menor que el valor crítico $\chi_{\alpha|n-1}$ .

$\begin{array}{l}H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha/2|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si }\chi^2<\chi^2_{\alpha/2|n-1}\text{ se rechaza } H_0 \\[3ex]H_1: \sigma^2> \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2< \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2<\chi^2_{\alpha|n-1}\text{ se rechaza } H_0\end{array}$

Los valores críticos del contraste de hipótesis para la varianza se obtienen de la tabla de la distribución chi-cuadrado. Ten en cuenta que los grados de libertad de la distribución chi-cuadrado son el tamaño de la muestra menos 1.

¿Qué es un contraste de hipótesis?

Hipótesis nula e hipótesis alternativa

Tipos de contrastes de hipótesis

Región de rechazo y región de aceptación de un contraste de hipótesis

Cómo hacer un contraste de hipótesis

Errores de un contraste de hipótesis

Estadísticos de contrastes de hipótesis

Contraste de hipótesis para la media

Contraste de hipótesis para la proporción

Contraste de hipótesis para la varianza

Deja un comentario Cancelar respuesta