▷ ¿Qué es la matriz de covarianza? (fórmula y ejemplo)

En este artículo se explica qué es la matriz de covarianza y cuál es su fórmula. Encontrarás cómo hacer la matriz de covarianza junto con un ejemplo resuelto, y las propiedades de las matrices de covarianza.

Índice

¿Qué es la matriz de covarianza?

La matriz de covarianza es una matriz cuadrada cuyos elementos son las varianzas y las covarianzas de las variables de estudio. De manera que los elementos de la diagonal principal de la matriz de covarianza son la varianza de cada variable, y los elementos restantes son las covarianzas entre las variables.

En estadística, la matriz de covarianza se utiliza para analizar la relación entre dos o más variables aleatorias. La matriz de covarianza es muy útil porque permite interpretar la correlación entre muchas variables rápidamente, ya que puedes ver los valores de todas las covarianzas de las variables al mismo tiempo.

El símbolo de la matriz de covarianza es la letra griega mayúscula sigma (Σ).

Cómo calcular la matriz de covarianza

Para calcular la matriz de covarianza de varias variables estadísticas se deben hacer los siguientes pasos:

Calcular las varianzas de todas las variables.
Calcular la covarianza de cada par de variables.
Formar la matriz de covarianza:

Se debe poner la varianza de la variable i en la diagonal principal de la matriz, concretamente en la posición i,i.
Se debe poner la covarianza entre las variables i y j en la posición i,j de la matriz.

Por lo tanto, la fórmula de la matriz de covarianza es la siguiente:

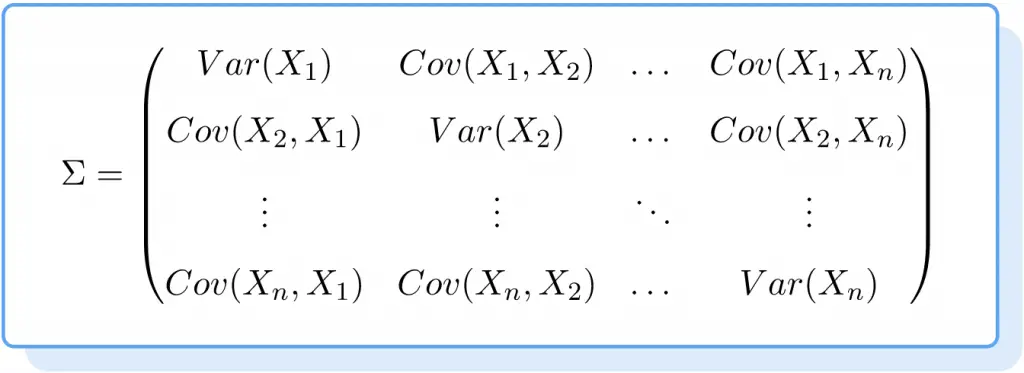
Ejemplo de matriz de covarianza

Después de ver la definición de la matriz de covarianza, a continuación tienes un ejercicio resuelto paso a paso para que veas cómo se hace este tipo de matriz.

Calcula la matriz de covarianza de las variables X, Y y Z, cuyos valores son:

X: 4, 7, 12, 5, 7
Y: 9, 15, 19, 6, 8
Z: 7, 2, 4, 6, 3

Lo primero que debemos hacer es determinar las varianzas de todas las variables:

$Var(X)=7,6$

$Var(Y)=23,44$

$Var(Z)=3,44$

➤ Ver: calculadora de la varianza

En segundo lugar, hallamos la covarianza entre cada par de variables:

$Cov(X,Y)=11,2$

$Cov(X,Z)=-2,6$

$Cov(Y,Z)=-4,36$

➤ Ver: calculadora de la covarianza

Y una vez tenemos todas las varianzas y covarianzas calculadas, solo queda hacer la matriz de covarianza. Para ello, ponemos los valores de las varianzas en la diagonal principal de la matriz y los valores de las covarianzas en su posición correspondiente:

$\Sigma=\begin{pmatrix}Var(X)&Cov(X,Y)&Cov(X,Z)\\[1.5ex]Cov(Y,X)&Var(Y)&Cov(Y,Z)\\[1.5ex]Cov(Z,X)&Cov(Z,Y)&Var(Z)\end{pmatrix}$

$\Sigma=\begin{pmatrix}7,6&11,2&-2,6\\[1.5ex]11,2&23,44&-4,36\\[1.5ex]-2,6&-4,36&3,44\end{pmatrix}$

Como puedes ver, al representar las varianzas y covarianzas en una matriz resulta muy sencillo hacer la interpretación de las variables. La variable con mayor dispersión es Y (23,44), por otro lado, las variables X e Y tienen una relación directa, mientras que las variables X y Z (y en consecuencia Y y Z) tienen una relación inversa.

Fíjate que la matriz de covarianza siempre es simétrica, ya que la covarianza entre dos variables no depende del orden de las variables. Por ejemplo, $Cov(X,Y)$ es igual a $Cov(Y,X).$

Además, la matriz de covarianza siempre será una matriz cuadrada y su dimensión será equivalente al número de variables. En este caso teníamos tres variables y por eso es una matriz 3×3, pero si hubiéramos tenido solo dos variables la matriz de covarianza hubiera sido 2×2.

Propiedades de la matriz de covarianza

La matriz de covarianza tiene las siguientes características:

La matriz de covarianza es una matriz cuadrada del orden del número de variables.
La matriz de covarianza es simétrica, lo que significa que la diagonal principal de la matriz es un eje de simetría.
La matriz de covarianza siempre es semidefinida positiva.
El determinante de la matriz de covarianza es igual o mayor que cero.

Matriz de covarianza