En este artículo encontrarás qué es una matriz de correlación, cuál es su fórmula, y cómo se interpreta un matriz de correlación. Además, podrás ver un ejemplo resuelto de la interpretación de una matriz de correlación.
Índice
¿Qué es una matriz de correlación?
La matriz de correlación es una matriz que contiene en la posición i,j el coeficiente de correlación entre las variables i y j.
Por lo tanto, la matriz de correlación es una matriz cuadrada llena de unos en la diagonal principal y el elemento de la fila i y la columna j consiste en el valor del coeficiente de correlación entre la variable i y la variable j.
De manera que la fórmula de la matriz de correlación es la siguiente:
Donde 
es el coeficiente de correlación entre las variables 
y 
Entonces, para poder hallar la matriz de correlación de un conjunto de datos es imprescindible que sepas cómo se calcula el coeficiente de correlación. Por si no lo recuerdas, en el siguiente enlace encontrarás cómo se hace junto con una calculadora online:
Una propiedad del coeficiente de correlación es que no importa el orden de las variables para su cálculo, es decir, que el coeficiente de correlación es equivalente al 
En consecuencia, la matriz de correlación es simétrica.
![\displaystyle R=\begin{pmatrix}1&r_{12}&r_{13}&\dots&r_{1n}\\[1.1ex] r_{12}&1&r_{23}&\dots&r_{2n}\\[1.1ex] r_{13}&r_{23}&1&\dots&r_{3n}\\[1.1ex] \vdots &\vdots &\vdots &\ddots &\vdots\\[1.1ex] r_{1n}&r_{2n}&r_{3n}&\dots&1\end{pmatrix}](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-59859390c0c74809d8b4464ee30d3258_l3.svg "Rendered by QuickLaTeX.com")
Para que tenga sentido realizar una matriz de correlación, el conjunto de datos estadísticos debe tener más de dos variables. De lo contrario solamente se debería determinar un coeficiente de correlación y la matriz de correlación carecería de significado.
Cómo hacer una matriz de correlación
Vista la definición de la matriz de correlación, vamos a ver cómo se hace este tipo de matriz estadística:
- Calcular el coeficiente de correlación de cada pareja de variables. Ten en cuenta que el orden de las variables no altera al resultado, por lo que solo se debe calcular una vez por cada pareja de variables.
- Hacer una matriz cuadrada de la misma dimensión que el número de variables de la serie de datos. Dicha matriz será la matriz de correlación.
- Poner un 1 en cada elemento de la diagonal principal de la matriz de correlación.
- Poner el coeficiente de correlación de las variables i,j en las posiciones i,j y j,i.
- Una vez la matriz de correlación ya está hecha, solo queda interpretar sus valores.
Ten presente que simplemente realizar la matriz de correlación no es suficiente, sino que luego debes interpretar sus valores y entender qué significan. En el siguiente apartado se explica cómo hacer una interpretación de una matriz de correlación.
Interpretación de la matriz de correlación
Para interpretar correctamente la matriz de correlación, hay que tener en cuenta que el valor del coeficiente de correlación puede ir desde -1 hasta +1:
- r=-1: las dos variables tienen una correlación perfecta negativa, por lo que se puede trazar una recta con pendiente negativa en la que se encuentren todos los puntos.
- -1<r<0: la correlación entre las dos variables es negativa, por lo tanto, cuando una variable aumenta la otra disminuye. Cuanto más cerca esté el valor de -1 significa que más relacionadas negativamente están las variables.
- r=0: la correlación entre las dos variables es muy débil, de hecho, la relación lineal entre ellas es nula. Esto no significa que las variables sean independientes, ya que podrían tener una relación no lineal.
- 0<r<1: la correlación entre las dos variables es positiva, cuanto más cerca esté el valor de +1 más fuerte es la relación entre las variables. En este caso, una variable tiende a incrementar su valor cuando la otra también aumenta.
- r=1: las dos variables tienen una correlación perfecta positiva, es decir, tienen una relación lineal positiva.
Entonces, para interpretar la matriz de correlación se debe hacer una interpretación de cada coeficiente de correlación y comparar los distintos resultados.
De esto modo, podrás ver cuáles son las variables que están más relacionadas entre sí, qué variables son más importantes, qué variables no tienen prácticamente ninguna relación con las demás, etc.
Ejemplo de matriz de correlación
Para acabar de entender en qué consiste la matriz de correlación y cómo se interpreta, en este apartado analizaremos un ejemplo de una matriz de correlación:
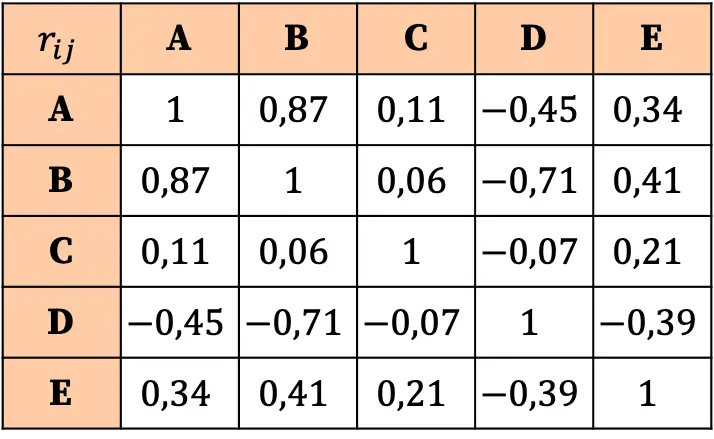
La interpretación de la matriz de correlación se basa en los valores de los coeficientes. Así pues, podemos ver que la correlación más fuerte es la relación entre la variable A y la variable B, ya que su correspondiente coeficiente es el mayor (0,87).
Por otro lado, la variable C prácticamente no tiene ninguna correlación con ninguna variable, ya que todos sus coeficientes son muy cercanos a cero y por tanto son muy débiles. Entonces, para simplificar el análisis, podríamos incluso considerar eliminar esta variable del estudio estadístico.
Asimismo, todas las relaciones de la variable D con las otras variables son negativas, lo que significa que la correlación entre la variable D y las otras variables es inversa. Esto no implica que se deba eliminar la variable, sino que simplemente la variable D está correlacionada negativamente.
Como puedes ver, la matriz de correlación es muy útil para resumir los datos y hacer un análisis global de la relación entre las diferentes variables del conjunto de datos.