▷ Límites de Control

En este post se explica qué es un límite de control y cuáles son los diferentes límites de control que tiene un gráfico de control. También podrás ver cómo se calculan los límites de control y, además, un ejemplo resuelto en el que se determinan los límites de control de un proceso.

Índice

¿Qué son los límites de control?

Los límites de control son las líneas horizontales de un gráfico de control que sirven para determinar si un proceso está controlado o no.

Un gráfico de control tiene dos límites de control: el límite de control superior y el inferior, que delimitan la zona de control por arriba y por abajo respectivamente.

Así pues, los límites de control son valores que se usan para indicar la zona de control de un proceso. Si la medición obtenida de un proceso está dentro de los límites de control, significa que el proceso está controlado. De lo contrario, se debe revisar la máquina o el proceso porque es probable que se haya desviado.

Tipos de límites de control

Los límites de control son:

Límite de Control Superior (LCS): es la línea que indica el valor máximo aceptado en el proceso.
Límite de Control Inferior (LCI): es la línea que indica el valor mínimo aceptado en el proceso.
Línea de Control Central: es la línea que representa el valor medio del gráfico. Cuanto más cerca estén los puntos de esta línea, significa que más estable es el proceso.

Cómo calcular los límites de control

Actualmente, los límites de control de un proceso se suelen calcular mediante un software informático que permite controlar el proceso, no obstante, también es importante que sepas cómo se calculan pues puede que necesites hallarlos de manera manual.

El cálculo de los límites de control de un diagrama de control depende del tipo de gráfico que se quiera realizar, pues los valores cambiarán según si es un gráfico de control para la media o para el rango.

El gráfico de control para la media es un gráfico en el que se evalúa la evolución de la media de un proceso. Así pues, la media de un conjunto de valores se calcula mediante la siguiente fórmula:

$\overline{X}=\cfrac{\displaystyle \sum_{i=1}^n x_i}{n}$

Donde:

$x_i$ es la medida número i.
$n$ es el número de medidas realizadas.

El valor central del gráfico de control para la media lo denotaremos como $\overline{\overline{X}}$ , que es el promedio de las muestras y se calcula con la siguiente expresión:

$\overline{\overline{X}}=\cfrac{\displaystyle \sum_{j=1}^m {\overline{X}_j}}{m}$

Donde:

$\overline{X}_j$ es la media de la muestra j.
$m$ es el número de muestras tomadas.

➤ Ver: Cálculo de la media aritmética

Por otro lado, el valor central del gráfico de control para el rango es el promedio de los rangos de todas las muestras tomadas:

$\overline{R}=\cfrac{\displaystyle \sum_{j=1}^m R_j}{m}$

Donde:

$R_j$ es el rango de la muestra j.
$m$ es el número de muestras tomadas.

➤ Ver: Cálculo del rango estadístico

Entonces, las fórmulas para calcular los límites de control de un gráfico de control son las siguientes:

Gráfico de control X

$\begin{array}{c}LCS=\overline{\overline{X}}+A_2\cdot \overline{R}\\[3ex]LCI=\overline{\overline{X}}-A_2\cdot \overline{R}\end{array}$

Gráfico de control R

$\begin{array}{c}LCS=D_4\cdot \overline{R}\\[3ex]LCI=D_3\cdot\overline{R}\end{array}$

Donde los valores de los parámetros A₂, D₃ y D₄ se pueden encontrar en la siguiente tabla:

Tamaño (n)	A₂	D₃	D₄
2	1,880	0,000	3,267
3	1,023	0,000	2,575
4	0,729	0,000	2,282
5	0,577	0,000	2,115
6	0,483	0,000	2,004
7	0,419	0,076	1,924
8	0,373	0,136	1,864
9	0,337	0,184	1,816
10	0,308	0,223	1,777

Ejemplo del cálculo de límites de control

Una empresa industrial quiere controlar la medida del diámetro de un cilindro para ver si su proceso de producción está bajo control. Para ello, toma una muestra de 5 cilindros cada 15 minutos y mide su diámetro. En la siguiente tabla se muestra el registro de las medidas.

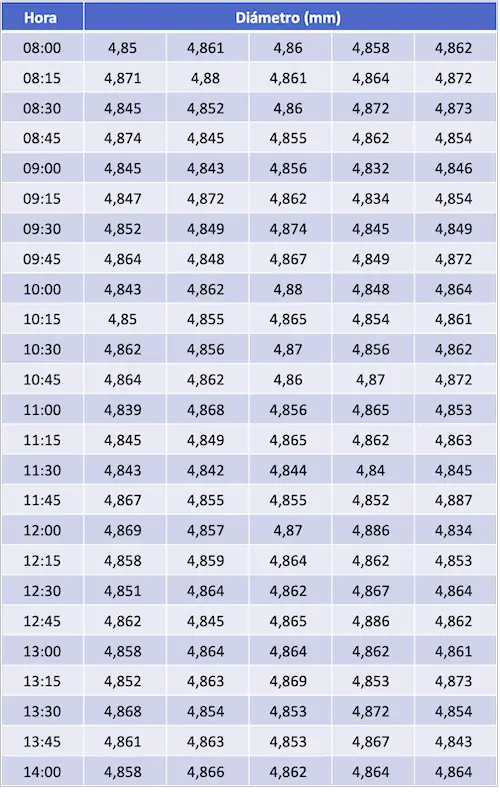
datos del ejemplo del gráfico de control

Para hallar los límites de control primero tenemos que sacar la media aritmética y el rango de cada conjunto de medidas:

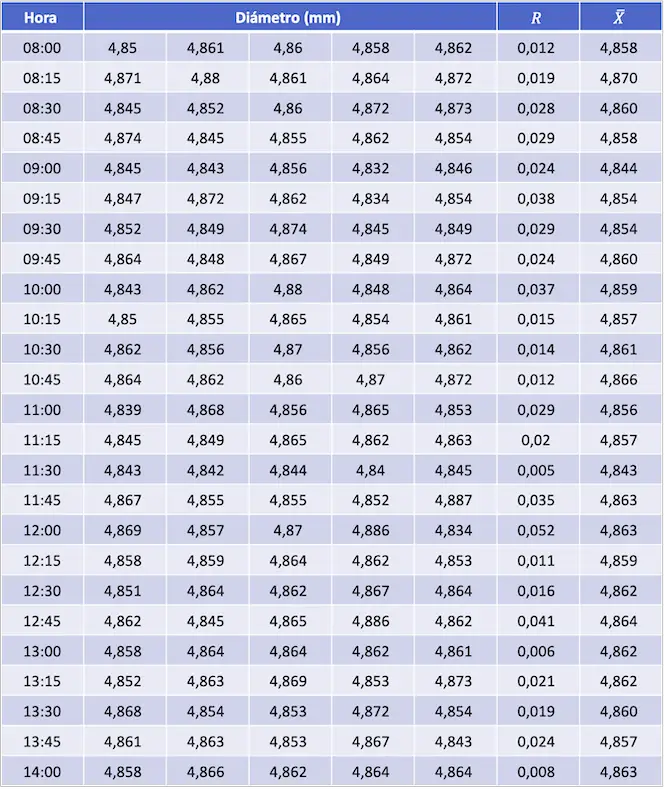
cálculos del ejemplo del gráfico de control

Ahora calculamos el promedio de las medias y de los rangos, que serán los valores centrales del diagrama de control para la media y para el rango respectivamente:

$\overline{\overline{X}}=\cfrac{\displaystyle \sum_{j=1}^m {\overline{X}_j}}{m}=4,8589$

$\overline{R}=\cfrac{\displaystyle \sum_{j=1}^m R_j}{m}=0,0227$

En este caso, cada muestra está formada por 5 medidas, por tanto, los coeficientes de las fórmulas de los límites de control son los siguientes:

$A_2=0,577$

$D_3=0$

$D_4=2,115$

Calculamos los límites de control superiores e inferiores del gráfico de control de la media y del rango:

Límites de control del gráfico de control X

$\begin{array}{c}LCS=\overline{\overline{X}}+A_2\cdot \overline{R}=4,8589+0,577\cdot 0,0227=4,8720\\[3ex]LCI=\overline{\overline{X}}-A_2\cdot \overline{R}=4,8589-0,577\cdot 0,0227=4,8458\end{array}$

Límites de control del gráfico de control R

$\begin{array}{c}LCS=D_4\cdot \overline{R}=2,115\cdot 0,0227=0,0481\\[3ex]LCI=D_3\cdot\overline{R}=0\cdot 0,0227=0\end{array}$

De modo que los gráficos de control del ejercicio son los siguientes:

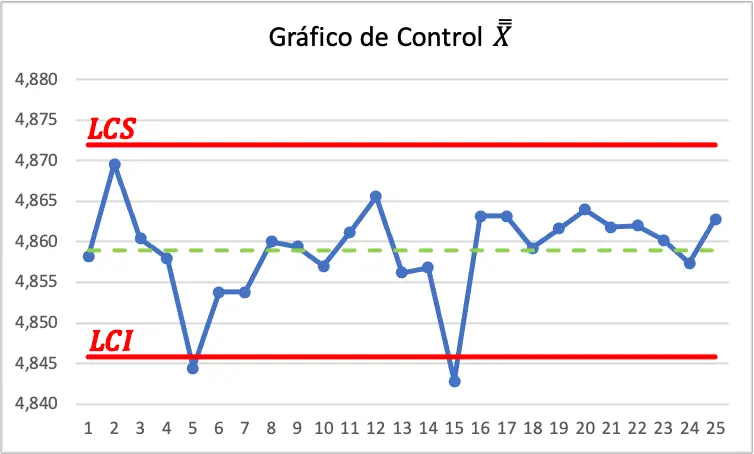
ejemplo del cálculo de los límites de control

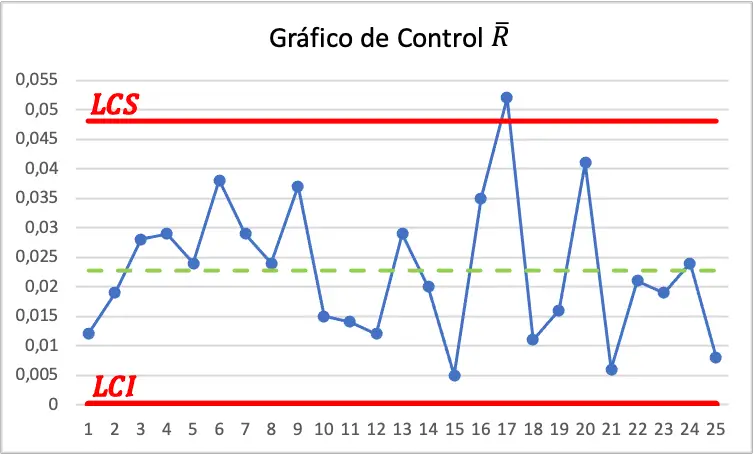
En el primer gráfico de control podemos ver que dos valores están por debajo del límite de control inferior, además, en el segundo gráfico de control también hay un valor por encima del límite de control superior. Por lo tanto, el proceso no está controlado.

¿Qué son los límites de control?

Tipos de límites de control

Cómo calcular los límites de control

Ejemplo del cálculo de límites de control

Deja un comentario Cancelar respuesta