Gráfico de control U

En este artículo te explicamos qué es un gráfico de control U, cuáles son sus características y para qué sirve. Además, podrás ver cómo se hace un gráfico de control U y un ejercicio resuelto paso a paso.

¿Qué es un gráfico de control U?

Un gráfico de control U, o simplemente gráfico U, es un gráfico en el que se representa el número de veces que ocurre un fenómeno por unidad de medida cuando esta es variable.

Por ejemplo, se puede utilizar un gráfico de control U para controlar el número de defectos por metro cuadrado de tela. A menudo no se pueden tomar muestras de tela con la misma superficie, por lo que cada muestra es diferente. Así pues, el gráfico U nos permite estudiar procesos que tienen un tamaño muestral variable.

Es importante destacar que en el gráfico de control U no se representa el número de unidades defectuosas, sino el número de defectos que tiene cada unidad, como en el gráfico C. Por otro lado, en un gráfico de control P o NP se controla la proporción y el número de productos defectuosos. Más abajo veremos las diferencias entre todos los tipos de gráficos de control.

Ten en cuenta que el modelo matemático de referencia del gráfico de control U es la distribución de Poisson, ya que se estudian el número de ocurrencias de un fenómeno por unidad de medida.

Cómo hacer un gráfico de control U

Ahora que ya sabemos la definición del gráfico de control U, vamos a ver cómo se hace este tipo de gráfico de control:

  1. Tomar muestras: primero se deben tomar diferentes muestras para ver la evolución del fenómeno que se quiere medir. Las muestras deben ser del mismo tamaño, además, se recomienda tomar un mínimo de 20 muestras.
  2. Determinar el número de veces que ocurre el fenómeno por unidad de medida: para cada muestra se debe determinar el número de veces que se repite el fenómeno que se pretende estudiar.
  3. Calcular el valor medio de ocurrencias: utilizando los datos recopilados, se debe calcular el promedio de las veces que ocurre el fenómeno por unidad de medida.

    4. \overline{u}=\cfrac{\text{N\'umero de veces que ocurre el fen\'omeno}}{\text{N\'umero total de unidades de todas las muestras}}

  4. Calcular los límites de control del gráfico U: luego se deben calcular los límites de control del gráfico U mediante las fórmulas mostradas a continuación. Ten presente que el valor de los límites de control varia según el tamaño de la muestra.

    5. \displaystyle LCS_i=\overline{u}+3\sqrt{\frac{\overline{u}}{n_i}

    \displaystyle LCI_i=\overline{u}-3\sqrt{\frac{\overline{u}}{n_i}

    Donde LCS_i y LCI_i son respectivamente el límite de control superior e inferior de la muestra i, \overline{u} es el valor medio de ocurrencias y n_i es el tamaño de la muestra i.

  5. Representar los valores en el gráfico: ahora se deben representar los valores recopilados junto con los límites de control calculados en una gráfica para hacer el gráfico de control U.
  6. Analizar el gráfico de control U: por último, solo falta comprobar que ningún valor del gráfico cae fuera de los límites de control y, por tanto, que el proceso está bajo control. De lo contrario se deberán tomar medidas para corregir el proceso.

Ejemplo de gráfico de control U

  • Una empresa industrial quiere controlar el número de defectos por m2 de tela. En la siguiente tabla se muestran las muestras analizadas y la cantidad de defectos encontrados. Realiza un gráfico de control U para estudiar el número de defectos.

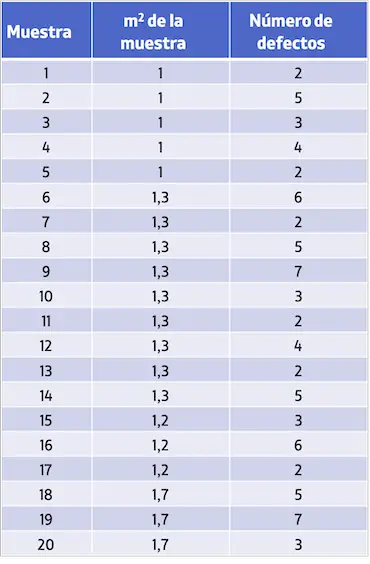
Para poder hacer la gráfica de control U, primero debemos calcular el valor medio del número de defectos por muestra:

\overline{u}=\cfrac{\text{N\'umero de veces que ocurre el fen\'omeno}}{\text{N\'umero total de unidades}}=\cfrac{78}{25,4}=3,07

Ahora tenemos que calcular los límites de control para cada muestra. A modo de ejemplo, a continuación se calcula los límites de control de la primera muestra:

\displaystyle LCS_1=\overline{u}+3\sqrt{\frac{\overline{u}}{n_1}}=3,07+3\sqrt{\frac{3,07}{1}}=8,33

\displaystyle LCI_1=\overline{u}-3\sqrt{\frac{\overline{u}}{n_1}}=3,07-3\sqrt{\frac{3,07}{1}}=-2,19

Todos los límites de control inferiores dan como resultado un número negativo, lo que no tiene sentido. Por lo tanto, fijaremos los límites de control inferiores a 0.

Así pues, los valores de los límites de control de cada muestra son los siguientes:

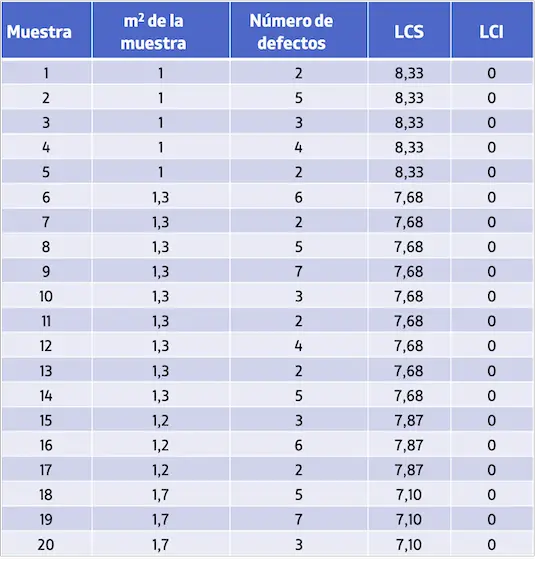
Por último, solo nos queda representar todos los valores en una gráfica para obtener el gráfico de control U:

gráfico de control U

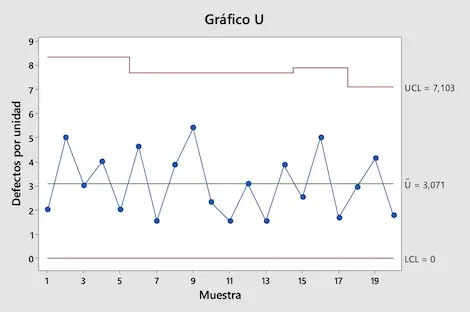
Como puedes ver en el gráfico U que hemos hecho, todos los valores están entre los límites de control. Por lo tanto, se concluye que el proceso de producción está bajo control.

Otros tipos de gráficos de control

Aparte del gráfico U, existen otros tipos de gráficos de control para atributos:

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Scroll al inicio