En este artículo te mostramos qué es un gráfico de control NP y para qué sirve. Además, podrás ver un ejercicio resuelto en el que te explicamos cómo se hace un gráfico de control NP.
Índice
¿Qué es un gráfico de control NP?
Un gráfico de control NP, o simplemente gráfico NP, es un gráfico en el que se representa el número de unidades defectuosas de varias muestras de tamaño constante.
Un gráfico de control NP sirve para controlar que el número de unidades defectuosas de un proceso no está fuera de los límites de control.
Por ejemplo, se puede utilizar un gráfico de control NP para analizar la evolución de productos defectuosos fabricados por un proceso de producción. De este modo podremos saber que hay algún problema en el proceso de producción cuando el número de productos defectuosos supere los límites de control.
Es importante destacar que, a diferencia de un gráfico de control P, el gráfico de control NP no monitoriza la proporción de unidades defectuosas, sino el número de unidades defectuosas. Además, el tamaño de todas las muestras debe ser el mismo.
Cómo hacer un gráfico de control NP
Los pasos que debes seguir para hacer un gráfico de control NP son los siguientes:
- Tomar muestras: en primer lugar, debes tomar diferentes muestras para ver la evolución del número de unidades defectuosas en el gráfico. Las muestras deben tener el mismo tamaño. Además, se recomienda tomar como mínimo 20 muestras y que el tamaño muestral sea mayor que 50.
- Contar el número de unidades defectuosas: para cada muestra, se debe determinar el número de unidades con al menos un defecto.
- Calcular el valor medio de la proporción: a partir de todos los elementos estudiados, debes calcular la proporción total de unidades defectuosas.
- Calcular los límites de control del gráfico NP: para cada muestra analizada, debes hallar sus límites de control utilizando las siguientes fórmulas:
- Representar los valores en el gráfico: ahora debes representar en una gráfica los valores del número de defectos obtenidos junto con los límites de control calculados en el paso anterior.
- Analizar el gráfico de control NP: por último, solo falta comprobar que ningún valor cae fuera de los límites de control del gráfico y que, por tanto, el proceso está bajo control. De lo contrario se deberán tomar medidas para corregir el proceso de producción.
Donde 
y 
son respectivamente el límite de control superior e inferior, 
es el valor medio de la proporción de defectos y 
es el tamaño de las muestras.
Ejemplo de gráfico de control NP
A continuación vamos a ver cómo se hace un gráfico de control NP mediante un ejemplo resuelto paso a paso.
- Una empresa industrial ha recogido muestras de 100 unidades y ha analizado cuántas piezas defectuosas había en cada muestra, puedes ver los valores registrados en la siguiente tabla. Realiza un gráfico de control NP con los datos obtenidos.
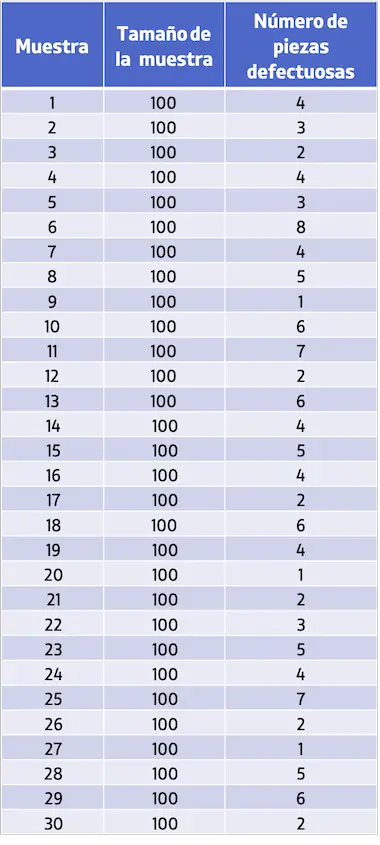
Como puedes ver, todas las muestras examinadas tienen el mismo tamaño y, además, el tamaño muestral es mayor que 50 unidades, por lo tanto, se cumplen las características para poder hacer un gráfico de control NP.
Así pues, lo primero que debemos calcular para hacer la gráfica NP es el promedio de unidades defectuosas. Para ello, basta con aplicar la siguiente fórmula:
Ahora calculamos los límites de control del gráfico NP con las fórmulas que hemos visto más arriba:
![\begin{aligned}\displaystyle LCS&=n\overline{p}+3\sqrt{n\overline{p}(1-\overline{p})}\\[2ex]&=100\cdot 0,039+3\sqrt{100\cdot 0,039(1-0,039)}\\[2ex]&=9,76\end{aligned}](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-e4e80d9af16465c4259b0f7cf3746b13_l3.svg "Rendered by QuickLaTeX.com")
![\begin{aligned}\displaystyle LCI&=n\overline{p}-3\sqrt{n\overline{p}(1-\overline{p})}\\[2ex]&=100\cdot 0,039-3\sqrt{100\cdot 0,039(1-0,039)}\\[2ex]&=-1,9\end{aligned}](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-aa6e060fb0ddf63e4722319c9df52caa_l3.svg "Rendered by QuickLaTeX.com")
El límite de control inferior ha salido negativo, lo que no tiene ningún sentido pues no se pueden fabricar unidades defectuosas negativas. Por lo tanto, fijamos el límite de control inferior en 0.
Una vez ya hemos calculado los límites de control, representamos todos los valores en el gráfico de control NP:
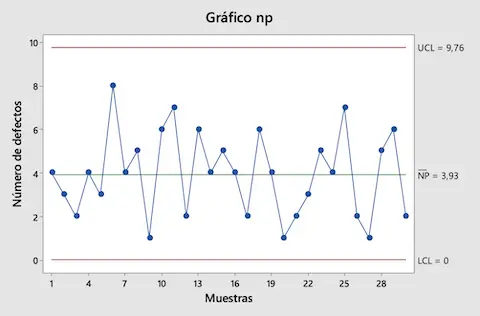
Como puedes ver en el gráfico NP, todos los valores recopilados de las muestras están entre los límites de control, por lo que se concluye que el proceso de producción está bajo control.
Otros tipos de gráficos de control
Aparte del gráfico de control NP, en gestión de calidad existen otros tipos de gráficos de control para atributos:
- Gráfico de control P: se controla la proporción de productos defectuosos.
- Gráfico de control C: se controla el número de defectos que ocurren.
- Gráfico de control U: se controla el número de defectos como en el gráfico C, pero el tamaño de la muestra es variable.