En este artículo encontrarás qué son las distribuciones simétricas, ejemplos de distribuciones simétricas y cómo determinar si una distribución es simétrica o asimétrica.
Índice
¿Qué es una distribución simétrica?
En estadística, una distribución simétrica es una distribución que tiene el mismo número de valores a la izquierda de la media que a la derecha de la media. Es decir, en una distribución simétrica la media es un eje de simetría.
Por ejemplo, la distribución normal es una distribución simétrica.
En todas las distribuciones simétricas la media es igual a la mediana. Pero si además la distribución es unimodal (la moda estadística es un único valor), la media, la mediana y la moda son equivalentes.
Lógicamente, para entender bien en qué consiste una distribución simétrica debes tener claro qué es la media, la mediana y la moda. Puedes repasar qué significan estos conceptos estadísticos aquí:
Ejemplos de distribuciones simétricas
Vista la definición de distribución simétrica, a continuación se muestra un ejemplo de este tipo de distribuciones:
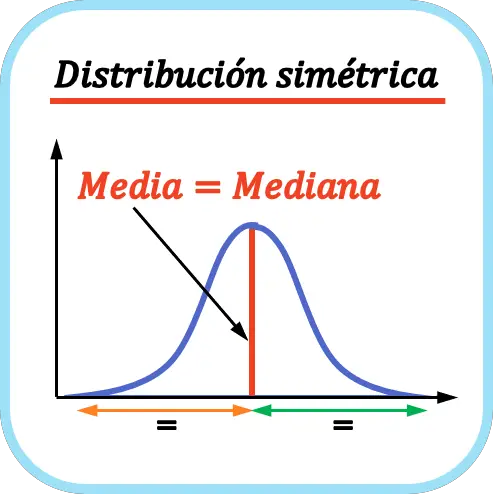
Tal y como se aprecia en la gráfica, la distribución es simétrica porque la media está justo en medio de todos los datos, es decir, la cola de la izquierda de la curva es igual que la cola de la derecha. En este caso la media, la mediana y la moda son iguales porque la moda es unimodal.
Dos ejemplos claros de dos tipos de distribuciones de probabilidad diferentes que son simétricas son la distribución normal y la distribución uniforme, ya que tienen el mismo número de valores a la izquierda y a la derecha de la media.
Por otro lado, una distribución también puede ser simétrica y ser bimodal, o dicho de otra forma, tener dos modas. Fíjate en el siguiente ejemplo:
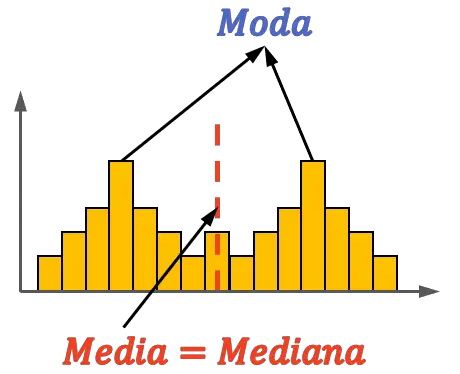
Como puedes ver en este otro ejemplo, una distribución bimodal también puede ser simétrica, pues puede tener la media y la mediana en el centro independientemente de los otros valores. Sin embargo, en este caso la moda no tiene por qué ser igual a la media y a la moda.
Otros tipos de distribuciones según su simetría
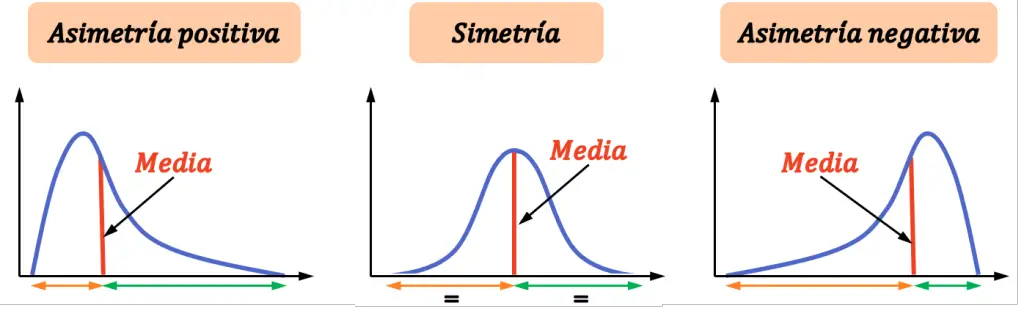
Aparte de las distribuciones que tienen simetría, existen dos tipos más de distribuciones que presentan asimetría.
- Distribución simétrica: la distribución tiene el mismo número de valores a la izquierda que a la derecha de la media.
- Distribución asimétrica positiva: la distribución tiene más valores diferentes a la derecha de la media que a su izquierda.
- Distribución asimétrica negativa: la distribución tiene más valores diferentes a la izquierda de la media que a su derecha.
Cómo saber si una distribución es simétrica
Para determinar si una distribución es simétrica o no, se debe calcular el coeficiente de asimetría de Pearson, cuya fórmula es:
Donde 
es el coeficiente de Pearson, 
la media aritmética, 
la moda (estadística) y 
la desviación típica.
Así pues, dependiendo del signo del coeficiente de asimetría de Pearson, la distribución será simétrica o asimétrica:
- Si el coeficiente de asimetría de Pearson es positivo, significa que la distribución es asimétrica positiva.
- Si el coeficiente de asimetría de Pearson es negativo, significa que la distribución es asimétrica negativa.
- Si el coeficiente de asimetría de Pearson es igual a cero, significa que la distribución es simétrica.
Sin embargo, el coeficiente de Pearson solo se puede calcular si la distribución es unimodal, en caso contrario debes utilizar el coeficiente de asimetría de Fisher, cuya fórmula es la siguiente:
Donde la media aritmética, la desviación estándar y 
el número total de datos.
La interpretación del coeficiente de asimetría Fisher es idéntica al coeficiente de Pearson: si es positivo significa que la distribución es asimétrica positiva, si es negativo la distribución es asimétrica negativa, y si es nulo implica que la distribución es simétrica.
