▷ Regresión lineal simple

En este artículo se explica qué es la regresión lineal simple en estadística y cómo se hace. Asimismo, encontrarás un ejercicio resuelto de la regresión lineal simple y, además, una calculadora online de la regresión lineal simple.

Índice

¿Qué es la regresión lineal simple?

La regresión lineal simple es un modelo estadístico usado para relacionar una variable independiente X con una variable dependiente Y. Es decir, en una regresión lineal simple solo hay dos variables (la variable explicativa X y la variable respuesta Y) y se intenta aproximar la relación que hay entre ambas variables.

Por lo tanto, la regresión lineal simple sirve para encontrar una ecuación que relacione dos variables de una manera lineal. Lógicamente, la relación entre las dos variables debe ser lineal, sino se debe utilizar otro tipo de modelo de regresión.

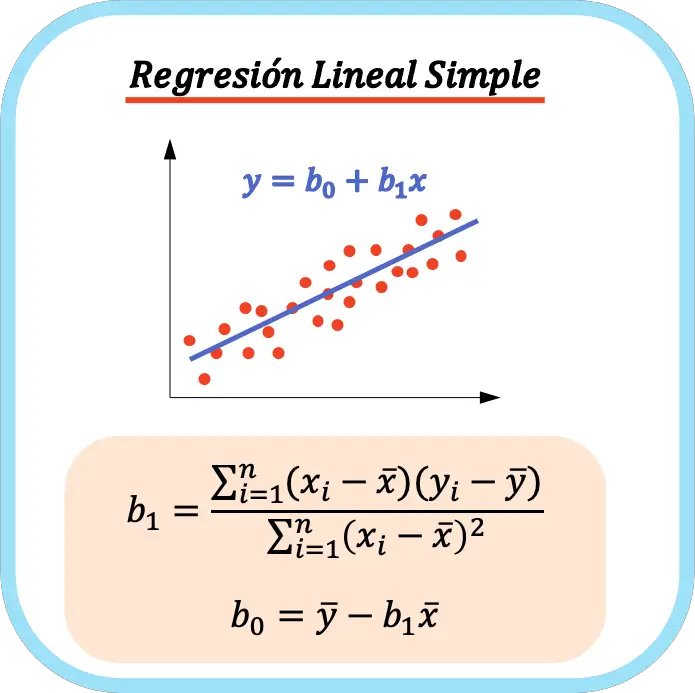
La ecuación de un modelo de regresión lineal simple está formada por dos coeficientes: la constante de la ecuación (b₀) y el coeficiente de la correlación entre las dos variables (b₁). Por lo tanto, la ecuación de un modelo de regresión lineal simple es y=b₀+b₁x.

$y=b_0+b_1x$

La ecuación de una regresión lineal simple se representa gráficamente como una línea recta, por lo que el coeficiente b₀ es la ordenada en el origen y el coeficiente b₁ es la pendiente de la recta.

Fórmulas de la regresión lineal simple

Las fórmulas para calcular los coeficientes de una regresión lineal simple son las siguientes:

👉 Puedes usar la calculadora que hay más abajo para calcular los coeficientes de una regresión lineal simple de cualquier conjunto de datos.

Evidentemente, la ecuación resultante del modelo de regresión lineal simple no podrá acertar el valor exacto de todas las observaciones, ya que este modelo simplemente trata de encontrar una ecuación que aproxime la relación entre las dos variables. Así pues, se define como residuo a la diferencia entre el valor real y el valor estimado por el modelo de la regresión lineal.

$e_i=y_i-\widehat{y}_i$

Ten en cuenta que el objetivo de un modelo de regresión lineal simple es minimizar los cuadrados de los residuos, es decir, la regresión lineal simple se basa en el criterio de los mínimos cuadrados.

Ejemplo resuelto de una regresión lineal simple

Para acabar de entender el método de la regresión lineal simple, a continuación tienes un ejemplo resuelto paso a paso en el que se calcula la ecuación de un modelo de regresión lineal simple de un conjunto de datos estadísticos.

Después de realizar un examen de estadística, se ha preguntado a cinco estudiantes cuántas horas de estudio dedicaron al examen, los datos se muestran en la tabla de abajo. Realiza un modelo de regresión lineal simple de los datos estadísticos recopilados para relacionar linealmente las horas de estudio con la nota obtenida.

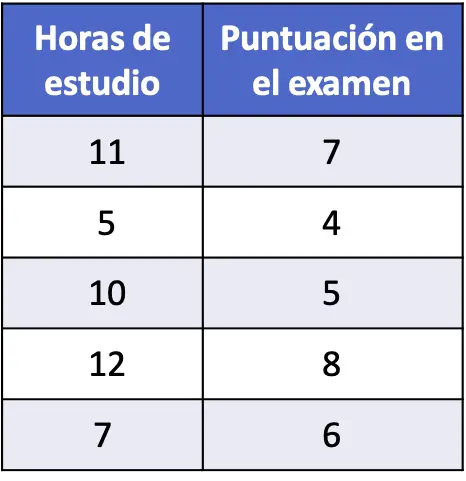
Para hacer un modelo de regresión lineal simple tenemos que determinar los coeficientes b₀ y b₁ de la ecuación y, para ello, tenemos que utilizar las fórmulas vistas en el apartado de arriba.

No obstante, para poder aplicar las fórmulas de la regresión lineal simple primero tenemos que calcular la media de la variable independiente y la media de la variable dependiente:

$\begin{array}{c}\overline{x}=\cfrac{11+5+10+12+7}{5}=9\\[4ex]\overline{y}=\cfrac{7+4+5+8+6}{5}=6\end{array}$

Ahora que ya sabemos las medias de las variables, calculamos el coeficiente b₁ del modelo usando su fórmula correspondiente:

$\begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[10ex] b_1=\cfrac{\begin{array}{c}(11-9)(7-6)+(5-9)(4-6)+(10-9)(5-6)+\\+(12-9)(8-6)+(7-9)(6-6)\end{array}}{(11-9)^2+(5-9)^2+(10-9)^2+(12-9)^2+(7-9)^2}\\[6ex]b_1=0,4412\end{array}$

Por último, calculamos el coeficiente b₀ del modelo empleando su fórmula correspondiente:

$\begin{array}{l}b_0=\overline{y}-b_1\overline{x}\\[3ex]b_0=6-0,4412\cdot 9 \\[3ex]b_0=2,0294\end{array}$

En definitiva, la ecuación del modelo de regresión lineal simple del problema es la siguiente:

$y=2,0294+0,4412x$

A continuación puedes ver la representación gráfica de la muestra de datos junto con la recta del modelo de regresión lineal simple:

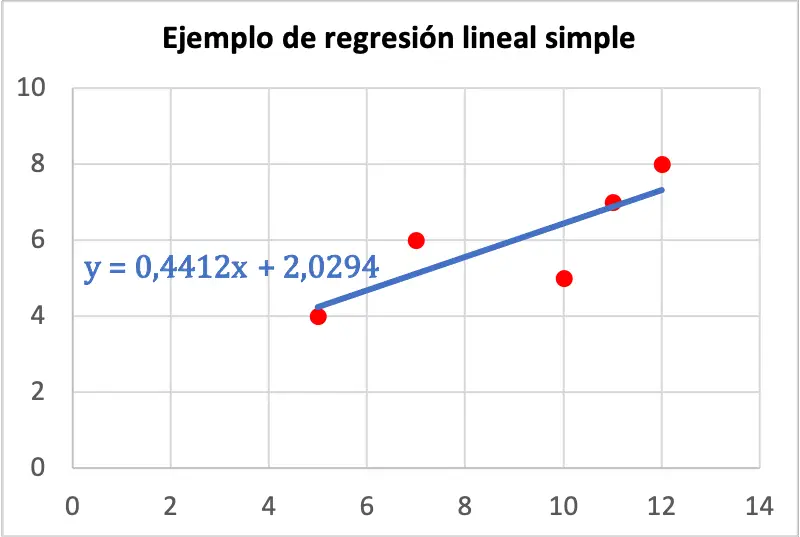
Para terminar, una vez hemos calculado la ecuación del modelo de regresión lineal simple, solo nos queda interpretar el resultado obtenido. Para ello, es imprescindible calcular el coeficiente de determinación del modelo de regresión, puedes ver cómo se hace buscando el artículo correspondiente en nuestra página web.

Supuestos de la regresión lineal simple

Para poder hacer una regresión lineal simple, se deben cumplir las siguientes hipótesis:

Independencia: los residuos observados deben ser independientes entre sí. Una manera común de garantizar la independencia del modelo es añadiendo aleatoriedad en el proceso de muestreo.
Homocedasticidad: debe haber homogeneidad en las varianzas de los residuos, es decir, la variabilidad de los residuos debe ser constante.

Normalidad: los residuos deben estar distribuidos normalmente, o dicho de otra forma, deben seguir una distribución normal de media 0.
Linealidad: la relación entre la variable independiente y la variable dependiente debe ser lineal.

Calculadora de la regresión lineal simple

Introduce una muestra de datos en la siguiente calculadora para ajustar un modelo de regresión lineal simple entre dos variables. Debes separar las parejas de datos, de manera que en el primer recuadro solo haya los valores de la variable independiente X y en el segundo recuadro únicamente estén los valores de la variable dependiente Y.

Los datos deben separase por un espacio e introducirse usando el punto como separador decimal.

Regresión lineal simple y múltiple

Finalmente, veremos cuál es la diferencia entre la regresión lineal simple y la regresión lineal múltiple, ya que son dos tipos de regresiones lineales que se utilizan frecuentemente en estadística.

La regresión lineal múltiple permite relacionar matemáticamente dos o más variables explicativas con una variable respuesta. Es decir, en la regresión lineal múltiple se hace un modelo en el que hay dos o más variables independientes.

Por lo tanto, la diferencia entre la regresión lineal simple y la regresión lineal múltiple es el número de variables independientes. En la regresión lineal simple solo hay una variable independiente, en cambio, en la regresión lineal múltiple hay dos o más variables independientes.

➤ Ver: Regresión lineal múltiple

Regresión lineal simple