En este post se explica en qué consiste la ley de Benford. Además, podrás ver cómo se descubrió la ley de Benford y cuáles son las aplicaciones de esta ley estadística.
Índice
¿Qué es la ley de Benford?
La ley de Benford, también llamada ley del primer dígito, es una ley estadística que dice que la probabilidad de que la primera cifra de un dato sea 1 es mayor que la probabilidad de que sea cualquier otro número.
Es decir, la ley de Benford dice que de un conjunto de datos numéricos que existen en la vida real, el número 1 es el número que más se repite como primera cifra de los datos.
Además, cuanto más grande sea el número, menos probable es de que este se encuentre en la primera posición. Por lo tanto, la primera cifra es más probable que sea un 1 que un 2, pero el 2 es más probable que el 3, el 3 es más probable que el 4 y así sucesivamente.
La ley de Benford recibe este nombre en honor al estadounidense Frank Benford. Aunque no fue él quien la inventó, Benford popularizó esta regla estadística. Más abajo veremos cuál es el origen de la ley de Benford.
Fórmula de la ley de Benford
La ley de Benford establece que la probabilidad de que la primera cifra sea un determinado número es igual al logaritmo de uno más uno partido por dicho número.
De modo que la fórmula de la ley de Benford es la siguiente:
![\begin{array}{c}\displaystyle P[X=d]=\log_{10}\left(1+\frac{1}{d}\right)\\[4ex]d=1,2,3,\ldots ,9\end{array}](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-d5f343d96429729f0ccf99c20b36f63f_l3.svg "Rendered by QuickLaTeX.com")
Por lo tanto, a partir de la fórmula de la ley de Benford se puede deducir la probabilidad para cada número de que sea la primera cifra de un dato. En la siguiente tabla puedes ver los porcentajes de todas las probabilidades:
| Dígito | Probabilidad de que sea la primera cifra |
|---|---|
| 1 | 30,1% |
| 2 | 17,6% |
| 3 | 12,5% |
| 4 | 9,7% |
| 5 | 7,9% |
| 6 | 6,7% |
| 7 | 5,8% |
| 8 | 5,1% |
| 9 | 4,6% |
Asimismo, a continuación puedes ver un histograma en el que se representan gráficamente todas las probabilidades de la ley de Benford:
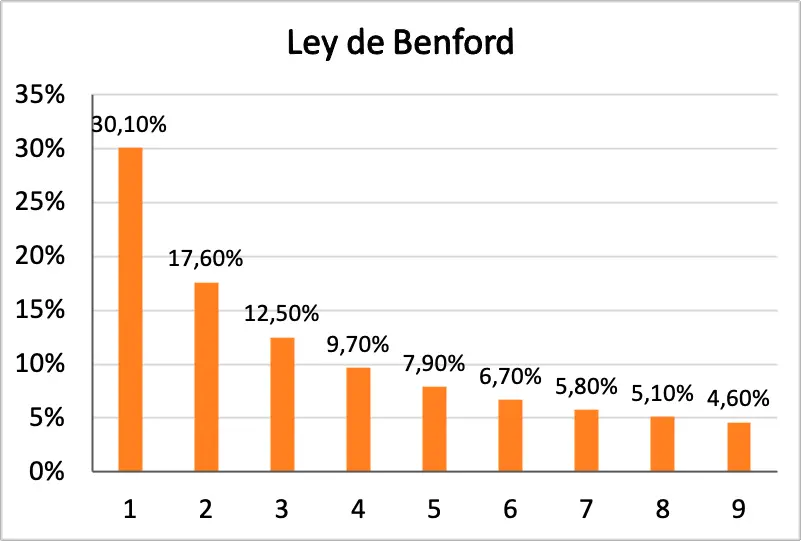
Historia de la ley de Benford
En 1881 el matemático Simon Newcomb dedujo la ley de Benford al descubrir que las primeras páginas de las tablas de los logaritmos estaban considerablemente más usadas que las páginas finales. Lo que significaba que los primeros dígitos de los números no son equiprobables, sino que el 1 era más frecuente que el 2, el 2 más frecuente que el 3, y así sucesivamente hasta el 9.
No obstante, Newcomb no dejo ninguna evidencia estadística de que se cumpliera esta regla, simplemente hizo una deducción a partir del desgaste de las tablas logarítmicas.
Más adelante, concretamente en 1938, el físico Frank Benford hizo la misma observación y, además, realizó un experimento para comprobarlo empíricamente. Sobre un conjunto de datos estadísticos de 20229 valores tomados de 20 muestras diferentes, hizo un estudio sobre cuál era el primer dígito de cada dato. De modo que, a partir de los resultados, demostró que la ley de Benford se cumplía y dedujo la fórmula que permitía calcular la probabilidad de que la primera cifra fuese un determinado número (hemos visto dicha fórmula más arriba).
En definitiva, aunque la ley de Benford la descubrió por primera vez Simon Newcomb, recibe el nombre de Frank Benford porque fue él quien comprobó esta ley estadística.
Aplicaciones de la ley de Benford
La ley de Benford es una ley estadística que tiene aplicaciones en ámbitos muy diferentes. Por ejemplo, la ley de Benford se utiliza mucho en economía, también en biología e, incluso, en política.
En economía, la ley de Benford se usa a menudo a para detectar la manipulación de los datos, ya que si un conjunto de datos no cumple con la ley de Benford es un indicio de que los datos han sido manipulados. Por ejemplo, esta ley se emplea para detectar posibles casos de fraude fiscal.
Cabe destacar que la ley de Benford no sirve para demostrar la veracidad de fenómenos aleatorios, ya que los resultados son equiprobables. Así pues, no se puede utilizar la regla de Benford para comprobar los resultados de la lotería.
Por otro lado, en genética se puede usar la ley de Benford para analizar las diferencias de longitud del genoma entre distintos tipos de organismos.
Por último, también se ha intentado detectar el fraude electoral aplicando la ley de Benford, a pesar de que la utilidad en este caso ha sido cuestionada.
