En este artículo se explica qué es la distribución de Weibull y para qué sirve. Además, podrás ver la representación gráfica de la distribución de Weibull y cuáles son las propiedades de este tipo de distribución de probabilidad.
Índice
¿Qué es la distribución de Weibull?
La distribución de Weibull es una distribución de probabilidad continua que queda definida por dos parámetros característicos: el parámetro de forma α y el parámetro de escala λ.
En estadística, la distribución de Weibull se usa principalmente para el análisis de supervivencia. Asimismo, la distribución de Weibull tiene muchas aplicaciones en diferentes ámbitos. Más abajo entraremos en detalle en el uso de la distribución de Weibull.
![]()
Dependiendo del autor, la distribución de Weibull también se puede parametrizar con tres parámetros. Entonces, se añade un tercer parámetro llamado valor umbral, el cual indica la abscisa en la que empieza la gráfica de la distribución.
La distribución de Weibull recibe el nombre del sueco Waloddi Weibull, quien la describió en detalle en 1951. No obstante, la distribución de Weibull fue descubierta por Maurice Fréchet en 1927 y aplicada por primera vez por Rosin y Rammler en 1933.
Gráfica de la distribución de Weibull
Una vez hemos visto la definición de la distribución de Weibull, vamos a ver cómo varia su representación gráfica en función de los valores de sus parámetros.
A continuación puedes ver varios ejemplos de cómo varia la gráfica de la función de densidad de la distribución de Weibull según el valor del parámetro de forma y el parámetro de escala.
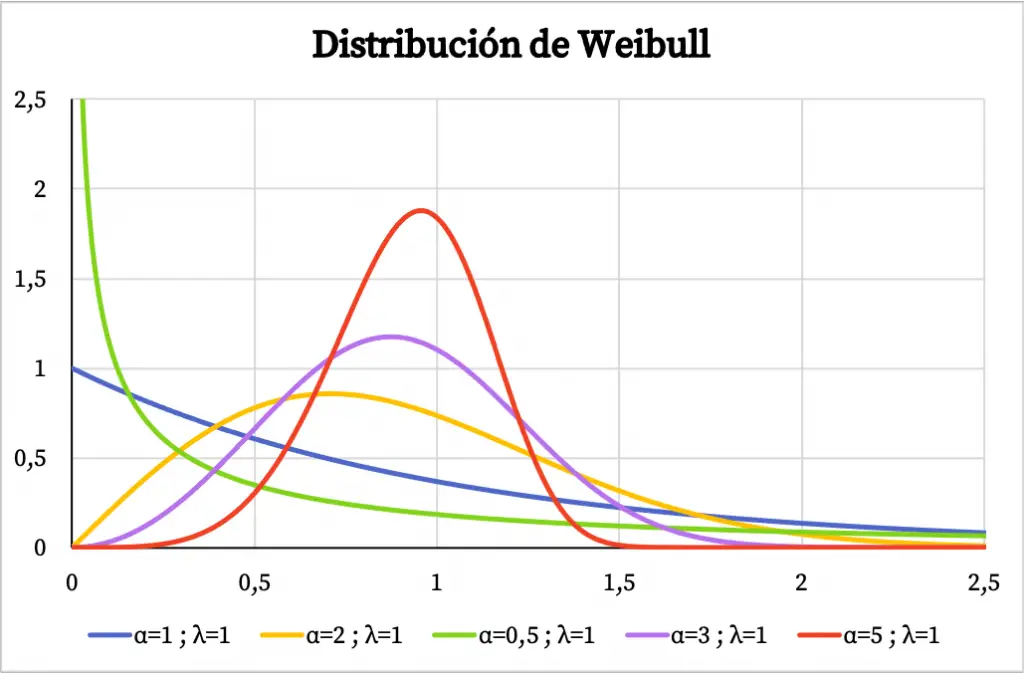
Cuando se utiliza la distribución de Weibull para modelar la tasa de fallos de un sistema en función del tiempo, el valor del parámetro de forma α significa lo siguiente:
- α<1: la tasa de fallos decrece con el tiempo.
- α=1: la tasa de fallos es constante en el tiempo.
- α>1: la tasa de fallos crece con el tiempo.
Por otro lado, en el siguiente gráfico puedes ver representada la función de probabilidad acumulada de la distribución de Weibull según sus valores característicos.
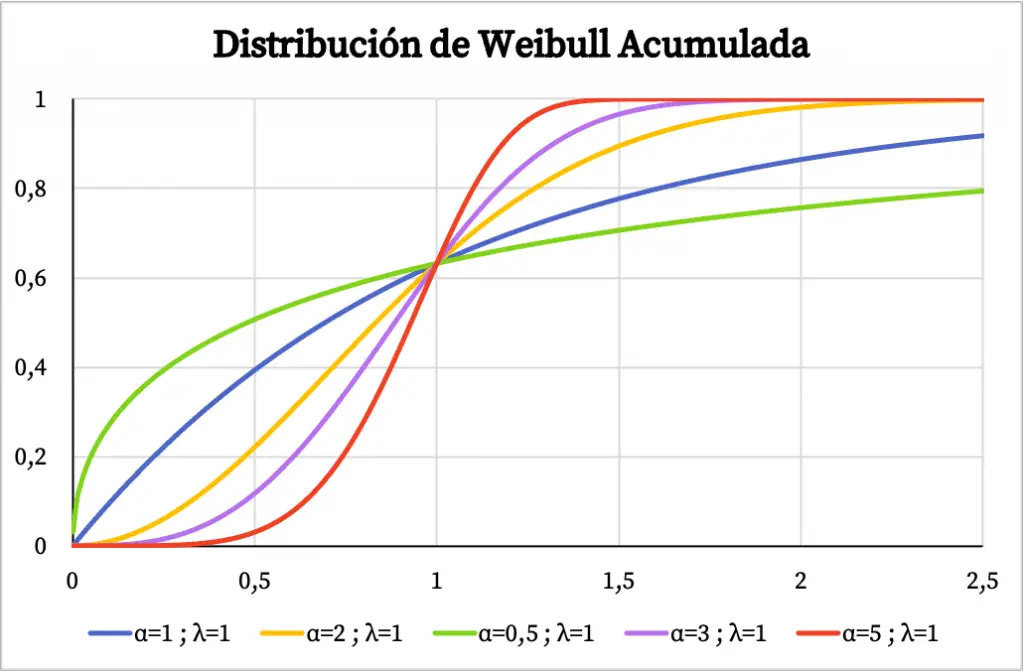
Características de la distribución de Weibull
La distribución de Weibull tiene las siguientes características:
- La distribución de Weibull tiene dos parámetros característicos que definen su gráfica: el parámetro de forma α y el parámetro de escala λ. Ambos parámetros son números reales positivos.
![Rendered by QuickLaTeX.com \begin{array}{c}\alpha >0\\[2ex]\lambda >0\\[2ex]\text{Weibull}(\alpha,\lambda)\end{array}](http://www.probabilidadyestadistica.net/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)
- La distribución de Weibull solo acepta valores de abscisas positivos.
![]()
- La media de la distribución de Weibull se calcula con la siguiente fórmula:
![Rendered by QuickLaTeX.com \displaystyle E[X]=\frac{1}{\lambda}\;\Gamma\left(1+\frac{1}{\alpha}\right)](http://www.probabilidadyestadistica.net/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)
- Por otro lado, la fórmula para hallar la varianza de la distribución de Weibull es la siguiente:
![Rendered by QuickLaTeX.com \displaystyle Var(X)=\frac{1}{\lambda^2}\left[\Gamma\left(1+\frac{2}{\alpha}\right)-\Gamma^2\left(1+\frac{1}{\alpha}\right)\right]](http://www.probabilidadyestadistica.net/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)
- La moda de una variable aleatoria que sigue una distribución de Weibull con α>1 se puede determinar mediante la siguiente expresión:

- La fórmula de la función de densidad de la distribución de Weibull es la siguiente:
![]()
- Asimismo, la fórmula de la función de probabilidad acumulada de la distribución de Weibull es la siguiente:
![]()
- El coeficiente de asimetría de la distribución de Weibull se calcula aplicando la siguiente fórmula:

- Por último, la fórmula que permite determinar el coeficiente de curtosis de la distribución de Weibull es la siguiente:

Donde ![]()
Aplicaciones de la distribución de Weibull
La distribución de Weibull tiene muchas aplicaciones, entre ellas destacan:
- En estadística aplicada, se utiliza la distribución de Weibull en el análisis de supervivencia.
- En ingeniería, se usa la distribución de Weibull para modelar funciones relacionadas con el tiempo de fabricación.
- En sistemas de radar, para simular la dispersión de la señal recibida.
- En el sector de los seguros, para modelar el tamaño de las pérdidas.
- En meteorología, por ejemplo, para modelar la frecuencia de las diferentes velocidades del viento.
