En este post se explica qué es la distribución de Pareto en estadística y para qué sirve. Asimismo, podrás ver la gráfica de la distribución de Pareto y las propiedades de este tipo de distribución de probabilidad.
Índice
¿Qué es la distribución de Pareto?
La distribución de Pareto es una distribución de probabilidad continua que se usa en estadística para modelizar el principio de Pareto. Por lo tanto, la distribución de Pareto es una distribución de probabilidad que tiene unos pocos valores cuya probabilidad de ocurrencia es mucho mayor que el resto de valores.
Recuerda que la ley de Pareto, también llamada regla del 80-20, es un principio estadístico que dice que la mayor parte de la causa de un fenómeno es debida a una pequeña parte de la población.
La distribución de Pareto tiene dos parámetros característicos: el parámetro de escala xm y el parámetro de forma α.
Originalmente, la distribución de Pareto se usaba para describir la distribución de la riqueza de la población, ya que la mayor parte era debida a una pequeña proporción de la población. Pero actualmente la distribución de Pareto tiene muchas aplicaciones, por ejemplo, en los controles de calidad, en economía, en ciencia, en el ámbito social, etc.
La distribución de Pareto recibe este nombre en honor al economista Vilfredo Pareto, que fue quien formuló la distribución. No obstante, se le conoce más por el diagrama de Pareto.
Gráfica de la distribución de Pareto
Ahora que ya sabemos al definición de la distribución de Pareto, vamos a ver varios ejemplos de distribuciones de Pareto representadas gráficamente.
Así pues, a continuación puedes cómo es la gráfica de la función de densidad de la distribución de Pareto según sus valores característicos:
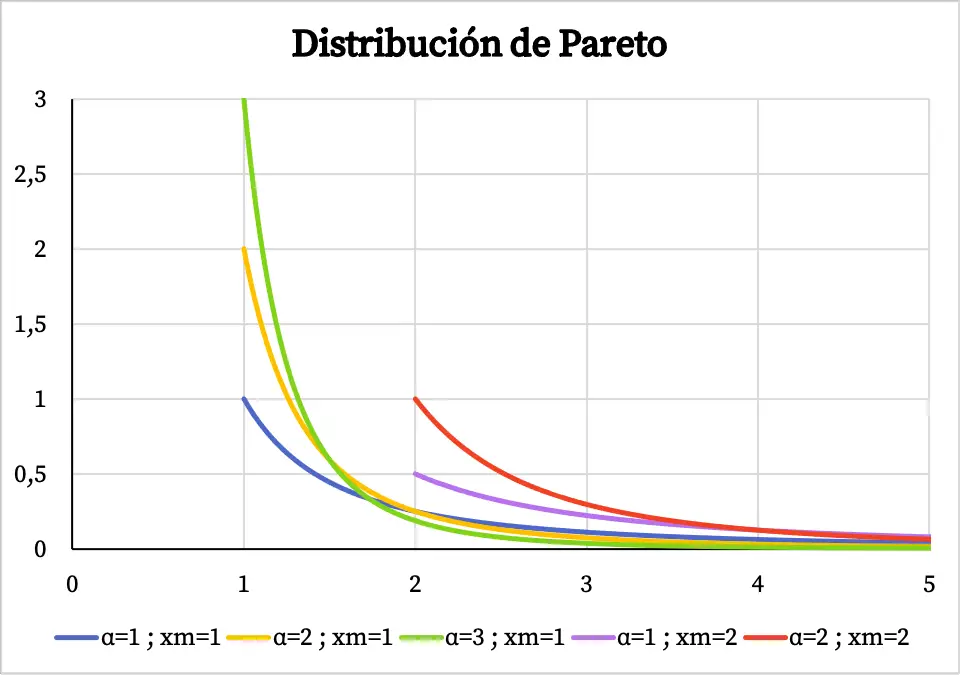
Fíjate que el dominio de la distribución de Pareto va desde el valor xm hasta +∞, por eso antes del valor de xm no existe la función de densidad.
Por otro lado, la gráfica de la función de probabilidad acumulada de la distribución de Pareto es la siguiente:
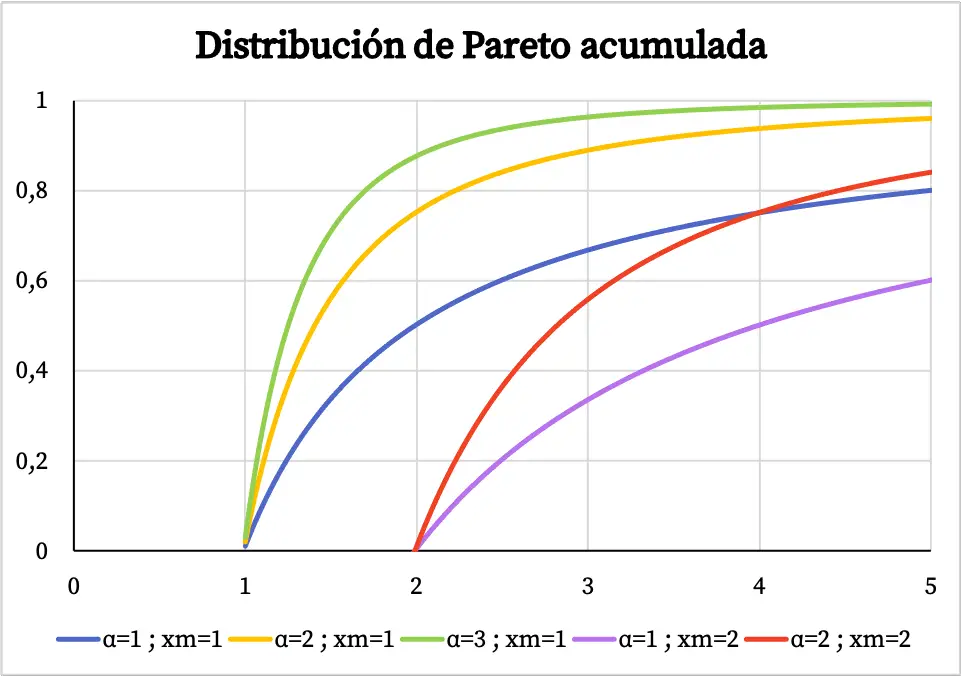
Características de la distribución de Pareto
A continuación se muestran las características más importantes de la distribución de Pareto relacionadas con la teoría de la probabilidad y la estadística.
- La distribución de Pareto tiene dos parámetros característicos que definen su curva: el parámetro de escala xm y el parámetro de forma α.
- El dominio de la distribución de Pareto son todos los números reales desde el parámetro de escala hasta más infinito.
- Si α es mayor que 1, la media de la distribución de Pareto es igual al producto de α por xm partido por α menos 1.
![E[X]=\cfrac{\alpha\cdot x_m}{\alpha-1}\quad\text{para } \alpha>1](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-bdaa15f35c3a3a052c952a3b18efc908_l3.svg "Rendered by QuickLaTeX.com")
- La varianza de la distribución de Pareto depende de los dos parámetros característicos de la distribución y se calcula con la siguiente fórmula:
- La mediana de la distribución de Pareto se puede determinar con la siguiente expresión:
![\displaystyle Me=x_\mathrm{m}\cdot \sqrt[\alpha]{2}](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-f9a558566cd8d12c86a8666ad9bddd6d_l3.svg "Rendered by QuickLaTeX.com")
- La moda de la distribución de Pareto es equivalente al parámetro de escala xm de la distribución.
- La fórmula de la función de densidad de la distribución de Pareto es la siguiente:
![\displaystyle P[X=x]=\frac{\alpha\cdot x_m^\alpha}{x^{\alpha+1}}\quad\text{para }x\geq x_m](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-15bcfdf78b636585860b15b05db0093f_l3.svg "Rendered by QuickLaTeX.com")
- Asimismo, la fórmula de la función de probabilidad acumulada de la distribución de Pareto es la siguiente:
![\displaystyle P[X\leq x]=1-\left(\frac{x_\mathrm{m}}{x}\right)^\alpha](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-5826c1b319c73a6a64ed850fe71b9975_l3.svg "Rendered by QuickLaTeX.com")
- El coeficiente de asimetría de la distribución de Pareto depende solamente del parámetro de forma α y su expresión es:
- El coeficiente de curtosis de la distribución de Pareto también varia en función del valor del parámetro α y se calcula mediante la siguiente fórmula:
La capacidad de aprender es infinita, gracias por la oportunidad.
¡Toda la razón Jorge! ¡Gracias por comentar!