En este artículo se explica qué es la bondad de ajuste en estadística. Asimismo, se muestra cómo medir la bondad de ajuste de un modelo de regresión y, además, podrás ver un ejercicio resuelto de la bondad de ajuste.
Índice
¿Qué es la bondad de ajuste?
En estadística, la bondad de ajuste es el grado de ajuste de un modelo de regresión a la muestra de datos. Es decir, la bondad de ajuste de un modelo de regresión se refiere al nivel de acoplamiento entre el conjunto de observaciones y los valores obtenidos mediante la regresión.
Por lo tanto, cuanto mayor sea la bondad de ajuste de un modelo de regresión, significa que mejor explica los datos estudiados. Así pues, nos interesa que el modelo estadístico esté cuanto más ajustado mejor.
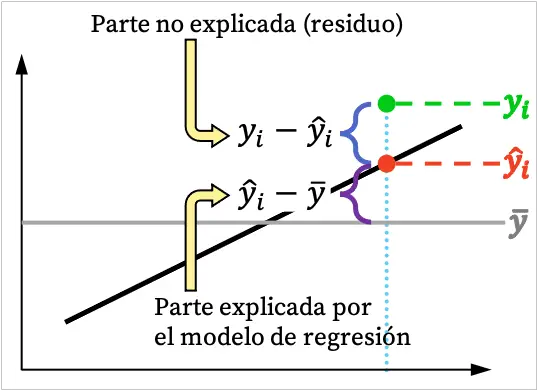
Como puedes ver en la imagen anterior, generalmente el valor de una observación no se puede explicar totalmente mediante el modelo de regresión. Pero, lógicamente, cuanto más pueda explicar el modelo de regresión del conjunto de datos, mejor ajustado estará el modelo. En definitiva, nos interesa un modelo de regresión lo más ajustado posible.
Bondad de ajuste de un modelo de regresión
Para determinar la bondad de ajuste de un modelo de regresión se suele utilizar el coeficiente de determinación, que es un coeficiente estadístico que indica el porcentaje explicado por el modelo de regresión. Así pues, cuanto mayor sea el coeficiente de determinación de un modelo, más ajustado estará el modelo a la muestra de datos.
![]()
No obstante, cabe destacar que cuantas más variables tenga un modelo de regresión, mayor será su coeficiente de determinación. Por eso también se suele utilizar el coeficiente de determinación ajustado para medir la calidad del ajuste de un modelo. El coeficiente de determinación ajustado es una variación del coeficiente anterior que indica el porcentaje explicado por el modelo de regresión penalizando por cada variable explicativa incluida en el modelo.
![]()
Por lo tanto, es mejor usar el coeficiente de determinación ajustado para comparar dos modelos que tienen un número de variables diferentes, ya que tiene en cuenta el número de variables incluidas en el modelo.
Por último, cabe destacar que también se puede emplear la prueba chi cuadrado para medir la calidad del ajuste de un modelo de regresión, aunque normalmente se suelen utilizar los valores de los dos coeficientes anteriores.
Ejemplo resuelto de la bondad de ajuste
Para terminar, vamos a ver un ejercicio resuelto de la bondad de ajuste para acabar de asimilar este concepto estadístico.
- Con la misma serie de datos, se realizan dos modelos de regresión lineales diferentes cuyos resultados puedes ver en la siguiente table ¿Cuál es el modelo que más nos conviene utilizar?
| Modelo de regresión 1 | Modelo de regresión 2 | |
|---|---|---|
| Coeficiente de determinación | 57% | 64% |
| Coeficiente de determinación ajustado | 49% | 43% |
| Número de variables explicativas | 3 | 7 |
En este caso, suponemos que los dos modelos cumplen con los supuestos previos de los modelos de regresión lineales y, por tanto, solo debemos analizar la bondad de ajuste de los modelos.
El modelo de regresión 2 tiene un coeficiente de determinación mayor que el modelo de regresión 1, por lo que a priori parece un modelo de regresión mejor pues es capaz de explicar mejor la muestra de datos.
Sin embargo, el modelo de regresión 2 tiene 7 variables independientes en el modelo, mientras que el modelo de regresión 1 solamente tiene 3. De modo que el modelo 2 será mucho más complicado y más difícil de interpretar que el primer modelo.
Además, si nos fijamos en el coeficiente de determinación ajustado, el cual tiene en cuenta el número de variables del modelo, el modelo de regresión 1 tiene un coeficiente de determinación ajustado mayor que el modelo de regresión 2.
En conclusión, es mejor utilizar el modelo de regresión 1, ya que su coeficiente de determinación ajustado es mayor que el del modelo de regresión 2. Aunque el modelo de regresión 2 tiene un coeficiente de determinación sin ajustar mayor, esto se debe a que se han incluido muchas más variables en el modelo, lo que hace aumentar el valor de dicho coeficiente pero dificulta la interpretación del modelo y, seguramente, provoque que la predicción de un valor nuevo sea peor.
Para comparar modelos con diferentes números de variables, es mejor utilizar el coeficiente de determinación ajustado porque penaliza por cada variable añadida al modelo. Como has podido ver en este ejemplo, según el coeficiente de determinación sin ajustar es mejor el modelo de regresión 2, no obstante, gracias al coeficiente de determinación ajustado podemos saber que el modelo de regresión 1 es en realidad mejor.
