▷ Análisis de la Varianza (ANOVA)

En este artículo se explica qué es el análisis de la varianza, también conocido como ANOVA, en estadística. Así pues, encontrarás cómo hacer un análisis de la varianza, en qué consiste la tabla ANOVA y un ejercicio resuelto paso a paso. Además, se muestran cuáles son los supuestos previos que se deben cumplir para poder realizar un análisis de la varianza y, por último, cuáles son las ventajas y las desventajas del análisis ANOVA.

Índice

¿Qué es el análisis de la varianza (ANOVA)?

En estadística, el análisis de la varianza, también llamado ANOVA (del inglés Analysis of Variance), es una técnica que permite comparar las varianzas entre las medias de diferentes muestras.

El análisis de la varianza (ANOVA) sirve para analizar si existe alguna diferencia entre las medias de más de dos poblaciones. De manera que el análisis de la varianza permite determinar si las medias poblacionales de dos o más grupos son diferentes analizando la variabilidad entre las medias de las muestras.

Por lo tanto, la hipótesis nula del análisis de la varianza es que las medias de todos los grupos analizados son iguales. Mientras que la hipótesis alternativa sostiene que al menos una de las medias es diferente.

$\begin{cases}H_0: \mu_1=\mu_2=\ldots=\mu_k=\mu\\[2ex]H_1: \exists \mu_i\neq \mu \quad i=1,2,\ldots, k\end{cases}$

Así pues, el análisis de la varianza es especialmente útil para comparar la media de más de dos grupos, ya que con este tipo de análisis se pueden estudiar las medias de todos los grupos a la vez, en lugar de ir comparando las medias por parejas. Más abajo veremos cuáles son las ventajas y las desventajas del análisis de la varianza.

Tabla ANOVA

El análisis de la varianza se resume en una tabla llamada tabla ANOVA cuyas fórmulas son las siguientes:

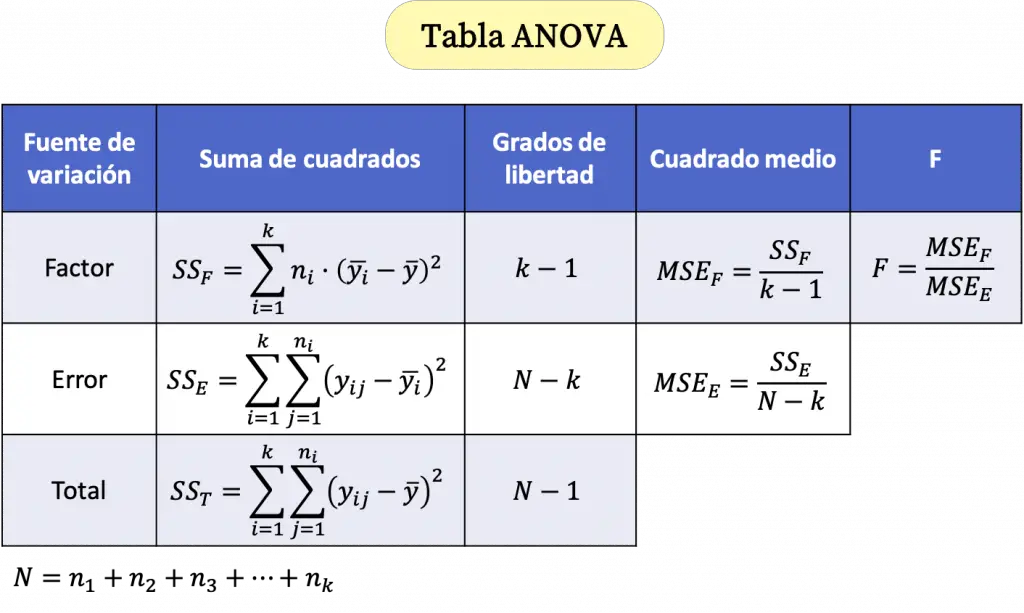
fórmulas del análisis de la varianza o ANOVA

Donde:

$n_i$ es el tamaño de la muestra i.
$N$ es el número total de observaciones.

$k$ es el número de grupos diferentes del análisis de la varianza.
$y_{ij}$ es el valor j del grupo i.
$\overline{y}_{i}$ es la media del grupo i.

$\overline{y}$ es la media de todos los datos analizados.

Ejemplo de un análisis de la varianza (ANOVA)

Para acabar de entender el concepto del ANOVA, vamos a ver cómo se hace un análisis de la varianza resolviendo un ejemplo paso a paso.

Se lleva a cabo un estudio estadístico para comparar las puntuaciones que sacan cuatro alumnos en tres asignaturas diferentes (A, B y C). En la siguiente tabla se detallan las puntuaciones obtenidas por cada alumno en un test cuya puntuación máxima es 20. Realiza un análisis de la varianza para comparar las notas obtenidas por cada alumno en cada asignatura.

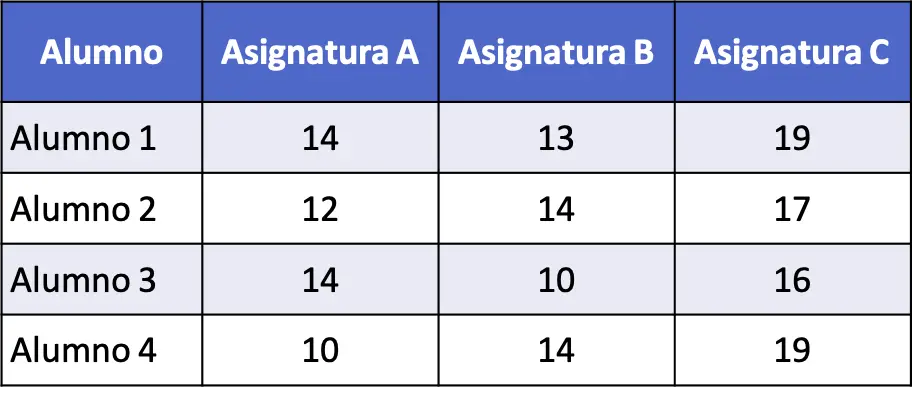
La hipótesis nula de este análisis de la varianza es que la media de las puntuaciones de las tres asignaturas son iguales. Por otro lado, la hipótesis nula es que alguna de estas medias es diferente.

$\begin{cases}H_0: \mu_A=\mu_B=\mu_C=\mu\\[2ex]H_1: \exists \mu_i\neq \mu \quad i=A, B, C\end{cases}$

Para llevar a cabo el análisis de la varianza, lo primero que debemos hacer es calcular la media de cada asignatura y la media total de los datos:

$\overline{y}_A=\cfrac{14+12+14+10}{4}=12,5$

$\overline{y}_B=\cfrac{13+14+10+14}{4}=12,75$

$\overline{y}_C=\cfrac{19+17+16+19}{4}=17,75$

$\overline{y}=\cfrac{14+12+14+10+13+14+10+14+19+17+16+19}{12}=14,33$

Una vez sabemos el valor de las medias, calculamos las sumas de los cuadrados utilizando las fórmulas del análisis de la varianza (ANOVA) vistas más arriba:

$\begin{aligned}\displaystyle SS_F&=\sum_{i=1}^k n_i(\overline{y}_i-\overline{y})^2\\[2ex] SS_F&= 4\cdot (12,5-14,33)^2+4\cdot (12,75-14,33)^2+4\cdot (17,75-14,33)^2\\[2ex] SS_F&=70,17\end{aligned}$

$\begin{aligned}\displaystyle SS_E=&\sum_{i=1}^k\sum_{j=1}^{n_i} (y_{ij}-\overline{y}_i)^2\\[2ex] \displaystyle SS_E=\ &(14-12,5)^2+(12-12,5)^2+(14-12,5)^2+(10-12,5)^2+\\&+(13-12,75)^2+(14-12,75)^2+(10-12,75)^2+(14-12,75)^2+\\&+(19-17,75)^2+(17-17,75)^2+(16-17,75)^2+(19-17,75)^2\\[2ex] SS_E=\ &28,50\end{aligned}$

$\begin{aligned}\displaystyle SS_T=&\sum_{i=1}^k\sum_{j=1}^{n_i} (y_{ij}-\overline{y})^2\\[2ex] \displaystyle SS_T= \ &(14-14,33)^2+(12-14,33)^2+(14-14,33)^2+(10-14,33)^2+\\&+(13-14,33)^2+(14-14,33)^2+(10-14,33)^2+(14-14,33)^2+\\&+(19-14,33)^2+(17-14,33)^2+(16-14,33)^2+(19-14,33)^2\\[2ex] SS_T= \ &98,67\end{aligned}$

Luego determinamos los grados de libertad del factor, del error y del total:

$GL_F=k-1=3-1=2$

$GL_E=N-k=12-3=9$

$GL_F=N-1=12-1=11$

Ahora calculamos los errores cuadráticos medios dividiendo las sumas de los cuadrados del factor y del error entre sus respectivos grados de libertad:

$MSE_F=\cfrac{SS_F}{GL_F}=\cfrac{70,17}{2}=35,08$

$MSE_R=\cfrac{SS_R}{GL_R}=\cfrac{28,50}{9}=3,17$

Y, finalmente, calculamos el valor del estadístico F dividiendo los dos errores calculados en el paso anterior:

$F=\cfrac{MSE_F}{MSE_R}=\cfrac{35,09}{3,17}=11,08$

En definitiva, la tabla ANOVA de los datos del ejemplo quedaría de la siguiente manera:

ejemplo de análisis de la varianza (ANOVA)

Una vez se han calculado todos los valores de la tabla ANOVA, solo falta interpretar los resultados obtenidos. Para ello, se debe hallar la probabilidad de obtener un valor mayor que el estadístico F en una distribución F de Snedecor con los grados de libertad correspondientes, es decir, debemos determinar el p-valor de la prueba:

$P[F>11,08]=0,004$

Por lo tanto, si tomamos un nivel de significación α=0,05 (el más habitual), tenemos que rechazar la hipótesis nula y aceptar la hipótesis alternativa, pues el p-valor de la prueba es menor que el nivel de significación. Esto quiere decir que como mínimo alguna de las medias de los grupos estudiados es diferente a las otras.

$0,004 < 0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \text{Se rechaza } H_0$

Cabe destacar que actualmente existen varios programas informáticos que permiten realizar un análisis de la varianza en tan solo unos segundos. No obstante, también es importante saber la teoría que hay detrás de los cálculos.

Supuestos del análisis de la varianza (ANOVA)

Para poder hacer un análisis de la varianza (ANOVA) se deben cumplir los siguientes requisitos:

Independencia: los valores observados son independientes entre sí. Una manera de garantizar la independencia de las observaciones es añadiendo aleatoriedad en el proceso de muestreo.

Homocedasticidad: debe haber homogeneidad en las varianzas, es decir, la variabilidad de los residuos es constante.
Normalidad: los residuos deben estar distribuidos normalmente, o dicho de otra forma, deben seguir una distribución normal.
Continuidad: la variable dependiente debe ser continua.

Tipos de análisis de la varianza (ANOVA)

Existen tres tipos de análisis de la varianza (ANOVA):

Análisis de la varianza de un factor (One-way ANOVA): en el análisis de la varianza solo hay un factor, es decir, solo hay una variable independiente.
Análisis de la varianza de dos factores (Two-way ANOVA): el análisis de la varianza tiene dos factores, por lo tanto, se analizan dos variables independientes y la interacción entre ellas.

Análisis multivariante de la varianza (MANOVA): en el análisis de la varianza hay más de una variable dependiente. Se pretende determinar si las variables independientes modifican su valor al variar las variables dependientes.

Ventajas y desventajas del análisis de la varianza (ANOVA)

Para terminar, veremos cuándo nos conviene utilizar el análisis de la varianza y, asimismo, cuáles son las limitaciones de este tipo de análisis estadístico.

La principal ventaja del análisis de la varianza (ANOVA) es que permite comparar más de dos grupos a la vez. A diferencia de la prueba t, en la que solo se puede analizar la media de una o dos muestras, el análisis de la varianza sirve para determinar si múltiples poblaciones tienen la misma media o no.

No obstante, el análisis de la varianza no nos dice cuál es el grupo del estudio que tiene una media distinta, solamente nos permite averiguar si hay alguna media significativamente diferente o si todas las medias son similares.

Asimismo, otra desventaja del análisis de la varianza es que se deben cumplir cuatro supuestos previos (vistos arriba) para poder realizar el análisis ANOVA, de lo contrario, las conclusiones extraídas pueden ser erróneas. Por lo tanto, siempre se debe verificar que el conjunto de datos estadísticos cumplen con estos cuatro requisitos.

Análisis de la varianza (ANOVA)