En este post encontrarás cómo calcular el promedio ponderado junto con un ejercicio resuelto. Además, podrás hallar el promedio ponderado de cualquier conjunto de datos con una calculadora online.
Índice
¿Qué es el promedio ponderado?
El promedio ponderado es una medida estadística que sirve para determinar un valor medio de un conjunto de datos otorgando a cada dato una importancia diferente.
El promedio ponderado se calcula sumando los productos de cada dato por su peso y luego dividiendo entre la suma de todos los pesos. No obstante, el promedio ponderado también se puede hallar mediante porcentajes, más abajo veremos en detalle cómo se calcula el promedio ponderado.
Fórmula del promedio ponderado
El promedio ponderado es igual al sumatorio de los productos de cada dato por su ponderación dividido por el sumatorio de todas las ponderaciones.
Por lo tanto, la fórmula del promedio ponderado es la siguiente:
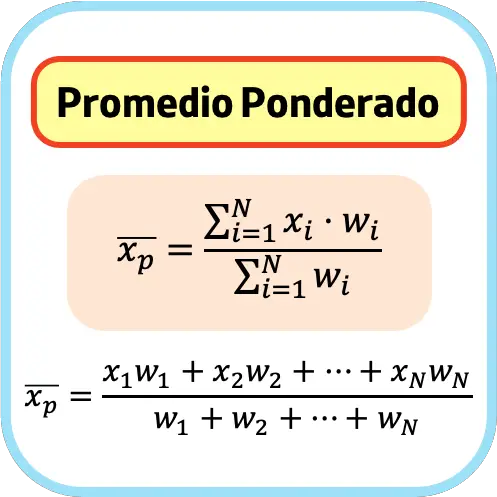
Donde:
es el promedio ponderado.- es el dato i de la serie de datos.
- es el peso o ponderación del dato i.
es el promedio ponderado.
es el dato i de la serie de datos.
es el peso o ponderación del dato i.👉 Puedes usar la calculadora que hay más abajo para calcular el promedio ponderado de cualquier conjunto de datos.
Así pues, cuanto más grande sea el peso de un dato, más importancia se le está otorgando en el cálculo del promedio ponderado. De manera que cuanto mayor sea el peso de un dato, más influirá en el resultado del promedio ponderado.
Cuando los pesos están expresados en forma de porcentaje la suma de todos los pesos da como resultado 1, por lo tanto, en este caso para sacar el promedio ponderado podemos simplemente multiplicar cada dato por su porcentaje correspondiente.
Por ejemplo, el promedio ponderado se utiliza para calcular la nota final de un estudiante. Para ello simplemente se debe multiplicar cada una de sus notas obtenidas en los diferentes exámenes por el porcentaje que vale cada examen respecto a la puntuación final.
Ejemplo del cálculo del promedio ponderado
- Un alumno de un instituto ha sacado las siguientes notas en la asignatura de matemáticas: un 7 en el examen parcial que cuenta 30%, un 9 en el trabajo en grupo que vale un 20%, un 6 en los ejercicios entregados en clase con una ponderación del 10%, y un 8 en el examen final que tiene un peso del 40%. ¿Cuál es su nota final de la asignatura?
Para determinar la nota del alumno debemos hallar el promedio ponderado con los valores que nos da el enunciado del problema. Para ello, aplicamos la fórmula del promedio ponderado:
La nota de cada entregable es el valor estadístico y su porcentaje corresponde al peso que tiene dicho valor. Por lo tanto, sustituimos los valores y los pesos en la fórmula y hacemos el cálculo del promedio ponderado:
En este caso, como las ponderaciones están expresadas en forma de porcentaje, podríamos haber multiplicado directamente cada nota por su porcentaje. A continuación tienes hecho este cálculo, así puedes comprobar que se obtiene el mismo resultado:
Calculadora del promedio ponderado
Introduce los datos de cualquier muestra estadística y sus respectivos pesos en la siguiente calculadora para calcular su promedio ponderado.
Introduce en el primer recuadro los datos estadísticos y en el segundo recuadro sus respectivos pesos, debes escribir los pesos en el mismo orden que los datos y en formato decimal. Todos los números deben separase por un espacio e introducirse usando el punto como separador decimal.
Promedio ponderado y promedio aritmético
Calcular el promedio ponderado y el promedio aritmético se hace de manera similar. En el cálculo del promedio ponderado se multiplica cada dato por su peso y luego se divide entre la suma de los pesos, por otro lado, en el promedio aritmético se suman todos los datos y se divide entre el número total de datos.
Por lo tanto, la diferencia entre el promedio ponderado y el promedio aritmético es que en el promedio ponderado cada dato tiene una importancia diferente, en cambio, en el promedio aritmético todos los datos tienen la misma importancia.
Ten en cuenta que si todos los pesos son iguales, el promedio ponderado es equivalente al promedio aritmético. A continuación tienes la demostración matemática:
![\begin{aligned}\overline{x_p}&=\cfrac{x_1\cdot w+x_2\cdot w+x_3\cdot w+\dots+x_N\cdot w}{w+w+w+\dots +w}\\[2ex]&= \cfrac{w\cdot (x_1+x_2+\dots+x_N)}{N\cdot w}=\\[2ex] &= \cfrac{x_1+x_2+\dots+x_N}{N}=\overline{x}\end{aligned}](https://www.probabilidadyestadistica.net/wp-content/ql-cache/quicklatex.com-9e5e91ad52039389f3f336e43f94aed1_l3.svg "Rendered by QuickLaTeX.com")