▷ Gráfico de control X-R

En este artículo encontrarás qué son los gráficos de control X-R y para qué sirven en estadística. También te explicamos cómo se hace un gráfico de control X-R y, además, podrás ver un ejemplo resuelto paso a paso.

Índice

¿Qué es un gráfico de control X-R?

El gráfico de control X-R, o simplemente gráfico X-R, es un gráfico que muestra la variación del valor de la media y el rango de una característica. Principalmente, el gráfico de control X-R se usa para controlar la media y el rango de un proceso de producción.

Así pues, en gestión de calidad el gráfico de control X-R permite analizar la evolución y comprobar que está bajo control una característica crítica de calidad, como por ejemplo la dimensión de una pieza o la temperatura de un horno.

En realidad, el gráfico de control X-R se divide en dos gráficos diferentes: el gráfico X y el gráfico R. El gráfico X sirve para controlar la media del proceso, mientras que el gráfico R se usa para monitorear el rango. Es por eso que el gráfico de control X-R también se llama gráfico de control de medias y rangos.

Ten en cuenta que el gráfico de control X-R es un tipo de gráfico de control por variables, pues permite controlar una característica continua.

Cómo hacer un gráfico de control X-R

Para hacer un gráfico de control X-R debes seguir los siguientes pasos:

Tomar muestras: en primer lugar, se deben tomar diferentes muestras de valores de la característica que se quiere controlar para hacer su seguimiento. Las muestras deben ser del mismo tamaño y se recomienda tomar un mínimo de 20 muestras.
Calcular la media: para cada muestra, se debe calcular el promedio de los valores registrados.

$\overline{X}=\cfrac{\displaystyle \sum_{i=1}^n x_i}{n}$

Calcular el promedio de las medias: después de determinar la media de cada muestra, se debe calcular el valor medio de todas las medias. Este será el valor central del gráfico X.

$\overline{\overline{X}}=\cfrac{\displaystyle \sum_{j=1}^m {\overline{X}_j}}{m}$

Calcular el rango: para cada muestra, debes hallar rango estadístico restando el valor máximo menos el valor mínimo.

$R=\text{M\'ax}-\text{M\'in}$

Calcular el promedio de los rangos: tras hallar el rango de cada muestra, se debe calcular el promedio de todos los rangos. Este será el valor central del gráfico R.

$\overline{R}=\cfrac{\displaystyle \sum_{j=1}^m R_j}{m}$

Calcular los límites de control del gráfico X-R: a partir de los valores calculados en los pasos anteriores, se deben calcular los límites de control del gráfico X y del gráfico R utilizando las siguientes fórmulas:

Gráfico de control X:

$\begin{array}{c}LCS=\overline{\overline{X}}+A_2\cdot \overline{R}\\[3ex]LCI=\overline{\overline{X}}-A_2\cdot \overline{R}\end{array}$

Gráfico de control R:

$\begin{array}{c}LCS=D_4\cdot \overline{R}\\[3ex]LCI=D_3\cdot\overline{R}\end{array}$

Donde los valores de los parámetros A₂, D₃ y D₄ los puedes encontrar en la tabla que hay más abajo.

Representar los valores en el gráfico: ahora solo falta representar los valores relacionados con la media en un gráfico y los valores relacionados con el rango en otro gráfico para obtener el gráfico X-R.
Analizar el gráfico de control X-R: por último, se debe comprobar que ningún valor del gráfico X-R cae fuera de los límites de control y que, por tanto, el proceso está bajo control. De lo contrario se deberán tomar medidas para corregir el proceso de producción.

Tamaño (n)	A₂	D₃	D₄
2	1,880	0,000	3,267
3	1,023	0,000	2,575
4	0,729	0,000	2,282
5	0,577	0,000	2,115
6	0,483	0,000	2,004
7	0,419	0,076	1,924
8	0,373	0,136	1,864
9	0,337	0,184	1,816
10	0,308	0,223	1,777

Ejemplo de gráfico de control X-R

Una empresa industrial quiere controlar la medida del diámetro de un cilindro para ver si su proceso de producción está bajo control. Para ello, se toma una muestra de 5 cilindros cada 15 minutos y mide su diámetro, en la siguiente tabla se muestra el registro de las medidas. Realiza un gráfico de control X-R para analizar el parámetro de calidad.

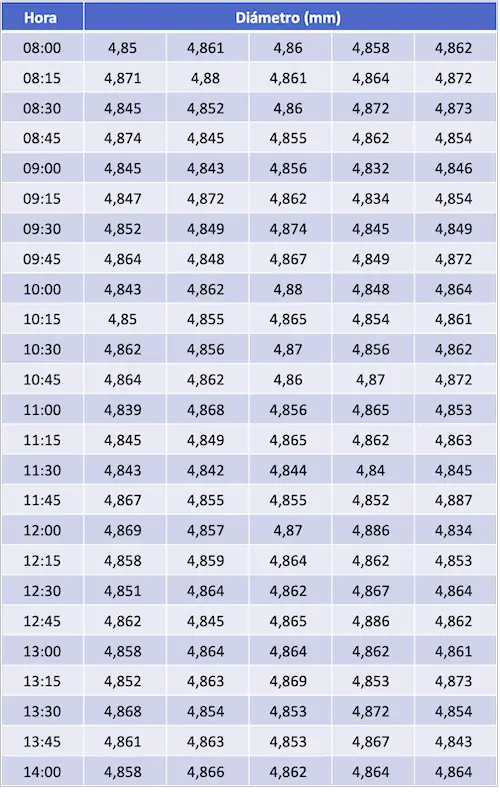
datos del ejemplo del gráfico de control

En primer lugar, tenemos que sacar la media aritmética y el rango de cada conjunto de medidas:

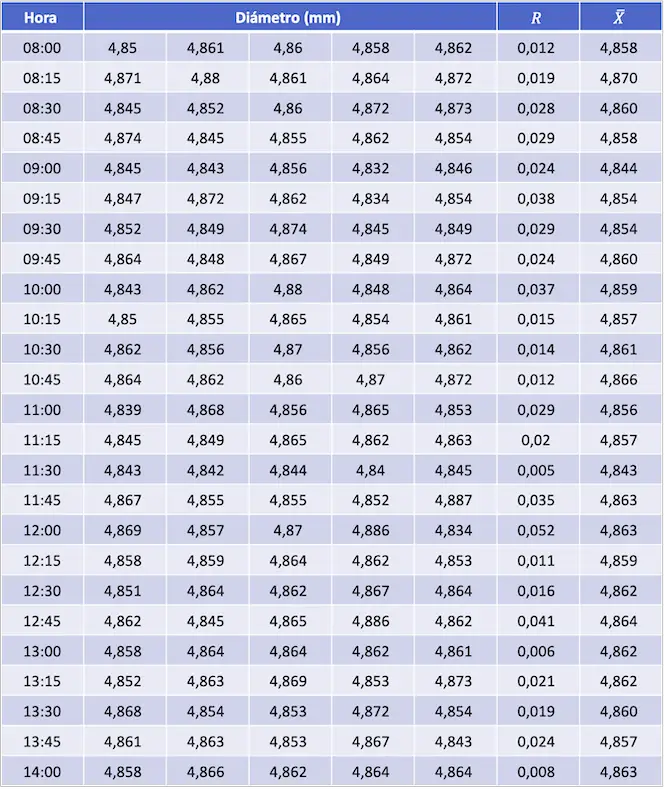
cálculos del ejemplo del gráfico de control

Ahora calculamos el promedio de las medias y de los rangos, que serán los valores centrales del diagrama de control para la media y para el rango respectivamente:

$\overline{\overline{X}}=\cfrac{\displaystyle \sum_{j=1}^m {\overline{X}_j}}{m}=4,8589$

$\overline{R}=\cfrac{\displaystyle \sum_{j=1}^m R_j}{m}=0,0227$

En este caso, cada muestra está formada por 5 medidas, por tanto, los coeficientes de las fórmulas de los límites de control son los siguientes (puedes ver los valores de los coeficientes en la tabla de más arriba):

$A_2=0,577$

$D_3=0$

$D_4=2,115$

Ahora calculamos los límites de control superiores e inferiores del gráfico de control X y R:

Límites de control del gráfico de control X

$\begin{array}{c}LCS=\overline{\overline{X}}+A_2\cdot \overline{R}=4,8589+0,577\cdot 0,0227=4,8720\\[3ex]LCI=\overline{\overline{X}}-A_2\cdot \overline{R}=4,8589-0,577\cdot 0,0227=4,8458\end{array}$

Límites de control del gráfico de control R

$\begin{array}{c}LCS=D_4\cdot \overline{R}=2,115\cdot 0,0227=0,0481\\[3ex]LCI=D_3\cdot\overline{R}=0\cdot 0,0227=0\end{array}$

De modo que el gráfico de control X-R del ejercicio es el siguiente:

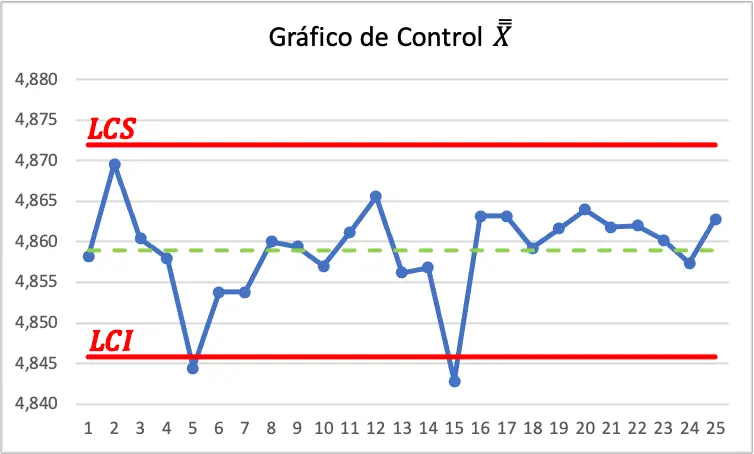
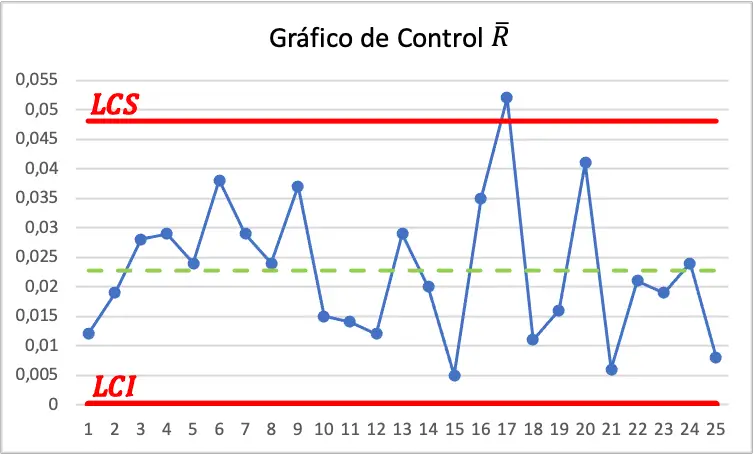
En el gráfico de control X podemos ver que dos valores están por debajo del límite de control inferior, además, en el gráfico de control R también hay un valor por encima del límite de control superior. Por lo tanto, el proceso no está controlado y se deben tomar medidas para disminuir la variabilidad de la media y del rango.

¿Qué es un gráfico de control X-R?

Cómo hacer un gráfico de control X-R

Ejemplo de gráfico de control X-R

Deja un comentario Cancelar respuesta