▷ Distribución Gamma

En este post se explica qué es la distribución gamma y para qué sirve. Así pues, encontrarás la definición de la distribución gamma, sus propiedades y cómo es su representación gráfica.

Índice

¿Qué es la distribución gamma?

La distribución gamma es una distribución de probabilidad continua definida por dos parámetros característicos, α y λ. Es decir, la distribución gamma depende del valor de sus dos parámetros: α es el parámetro de forma y λ es el parámetro de escala.

El símbolo de la distribución gamma es la letra griega mayúscula Γ. Por lo tanto, si una variable aleatoria sigue una distribución gamma se escribe de la siguiente manera:

$X\sim \Gamma(\alpha,\lambda)$

La distribución gamma también se puede parametrizar usando el parámetro de forma k=α y el parámetro inverso de escala θ=1/λ. En cualquier caso, los dos parámetros que definen la distribución gamma son números reales positivos.

En general, la distribución gamma se utiliza para modelar conjuntos de datos que son asimétricos a la derecha, de manera que existe una mayor concentración de datos en la parte izquierda de la gráfica. Por ejemplo, la distribución gamma se usa para modelar la fiabilidad de componentes eléctricos.

Gráfica de la distribución gamma

La gráfica de la distribución gamma depende de los valores de sus parámetros característicos. A continuación puedes ver cómo varia la función de densidad de la distribución gamma según el parámetro de forma y el parámetro de escala.

Por otro lado, abajo puedes ver la gráfica de la función de probabilidad acumulada de la distribución gamma:

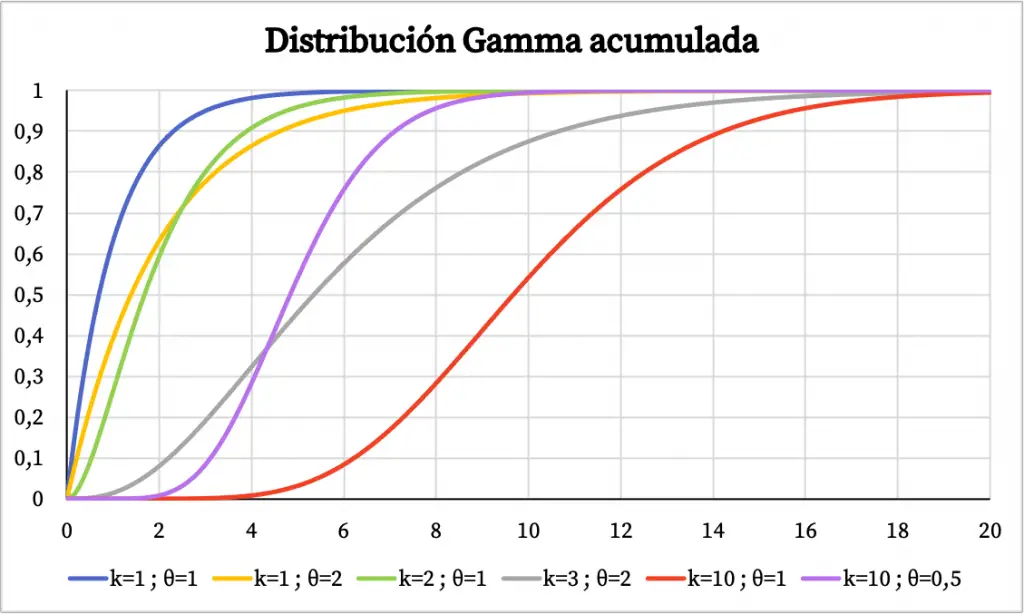
Características de la distribución gamma

A continuación vamos a ver cuáles son las características de la distribución gamma.

La gráfica de la distribución gamma queda definida completamente por sus dos parámetros característicos: α es el parámetro de forma y λ es el parámetro de escala.

$\alpha , \lambda >0$

El dominio de la distribución gamma son todos los números positivos.

$x\in (0,+\infty)$

La media de la distribución gamma es igual al cociente entre el parámetro de forma y el parámetro de escala, esto es, α/λ.

$E[X]=\cfrac{\alpha}{\lambda}$

La varianza de la distribución gamma es equivalente al parámetro de forma partido por el cuadrado del parámetro de escala.

$Var(X)=\cfrac{\alpha}{\lambda^2}$

Para valores de α menores que 1, la moda es 0. Pero si α es igual o mayor que 1, la moda de la distribución gamma se puede calcular con la siguiente fórmula:

$\begin{array}{c}Mo=0 \qquad \text{para } \alpha<1\\[2ex]Mo=\cfrac{\alpha-1}{\lambda} \qquad \text{para } \alpha\geq1\end{array}$

La fórmula de la función de densidad de la distribución gamma es la siguiente:

$\displaystyle f(x)=\frac{\lambda(\lambda x)^{\alpha-1}e^{-\lambda x}}{\Gamma(\alpha)}$

Donde Γ es la función gamma, que se define como:

$\displaystyle \Gamma(\alpha)=\int_0^\infty t^{\alpha-1}e^{-t}dt$

La fórmula de la distribución acumulada de una variable aleatoria definida por una distribución gamma es la siguiente:

$\displaystyle F(x)=\int_0^x\frac{\lambda(\lambda y)^{\alpha-1}e^{-\lambda y}}{\Gamma(\alpha)}\;dy$

Si el parámetro de forma α es 1, entonces la distribución gamma es equivalente a una distribución exponencial con el mismo parámetro de escala λ.

$X\sim \Gamma(1,\lambda) \ \color{orange}\bm{\longrightarrow}\color{black} \ X\sim \text{Exp}(\lambda)$

Cuando el parámetro de escala λ es un medio, entonces la distribución gamma es un caso particular de la distribución chi-cuadrado.

$\displaystyle X\sim \Gamma\left(\frac{n}{2},\frac{1}{2}\right) \text{con } n\in \mathbb{N}\ \color{orange}\bm{\longrightarrow}\color{black} \ X\sim \chi_n^2$

Distribución gamma

¿Qué es la distribución gamma?

Gráfica de la distribución gamma

Características de la distribución gamma

Deja un comentario Cancelar respuesta