En este artículo se explica qué son las distribuciones de frecuencias y cómo se hacen. También encontrarás ejemplos explicados paso a paso de distribuciones de frecuencias y, además, podrás practicar con ejercicios resueltos.
Índice
¿Qué es una distribución de frecuencias?
En estadística, la distribución de frecuencias es una tabla en la que se agrupan los diferentes valores de una muestra en filas y en cada columna se muestra un tipo de frecuencia de cada valor. Por lo tanto, la distribución de frecuencias sirve para mostrar todos los tipos de frecuencias de un conjunto de datos.
En concreto, una distribución de frecuencias incluye la frecuencia absoluta, la frecuencia absoluta acumulada, la frecuencia relativa y la frecuencia relativa acumulada.
Una de las características de las distribuciones de frecuencias es que son muy útiles para resumir una muestra estadística tanto de una variable cuantitativa como de una variable cualitativa.
Cómo hacer una distribución de frecuencias
Para hacer una distribución de frecuencias debes seguir los siguientes pasos:
- Organizar los datos en diferentes categorías y construir una tabla en la que cada fila corresponda a una categoría.
- Calcular la frecuencia absoluta de cada categoría en la segunda columna de la tabla.
- Calcular la frecuencia absoluta acumulada de cada categoría en la tercera columna de la tabla.
- Calcular la frecuencia relativa de cada categoría en la cuarta columna de la tabla.
- Calcular la frecuencia relativa acumulada de cada categoría en la quinta columna de la tabla.
- Opcionalmente, se pueden añadir dos columnas en las que se calculan la frecuencia relativa y la frecuencia relativa acumulada en forma de porcentaje, para ello simplemente debes multiplicar ambas columnas por 100.
Ejemplo de distribución de frecuencias
Una vez hemos visto la definición de distribución de frecuencias y la teoría sobre cómo se construye, en este apartado se resuelve un ejemplo paso a paso.
- Las notas obtenidas en la asignatura de estadística en una clase de 30 alumnos son las siguientes. Construye una distribución de frecuencias del conjunto de datos.
![]()
![]()
![]()
Como todos los números solo pueden ser enteros, se trata de una variable discreta. Por lo tanto, no es necesario agrupar el conjunto de datos en intervalos.
Entonces, para hacer una distribución de frecuencias tenemos que construir una tabla en la que cada valor diferente será una fila y luego tenemos que hallar la frecuencia absoluta de cada valor:
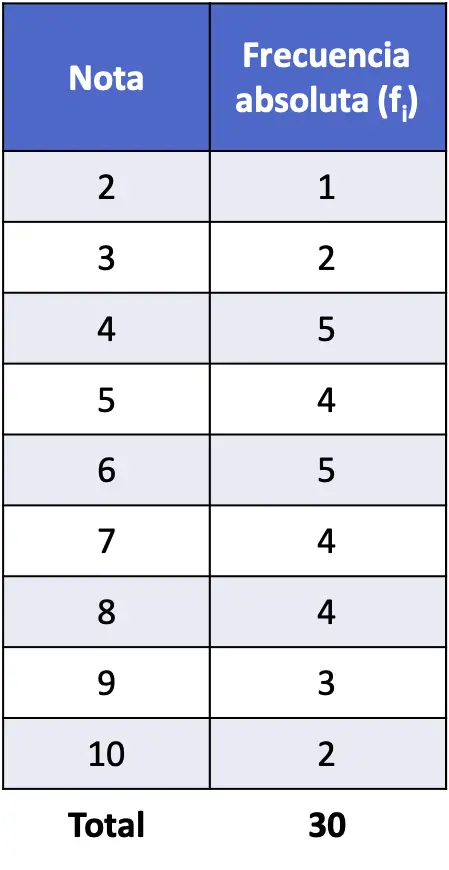
Fíjate que la suma de todas las frecuencias absolutas es equivalente al número total de datos. Si no se cumple esta regla, significa que te has olvidado de contar algún dato.
Ahora que ya sabemos la frecuencia absoluta, tenemos que calcular la frecuencia absoluta acumulada. Para este cálculo tenemos dos opciones: o sumamos la frecuencia absoluta del valor más todas las frecuencias absolutas de los valores menores, o por otro lado, sumamos la frecuencia absoluta del valor más la frecuencia absoluta acumulada del valor anterior.
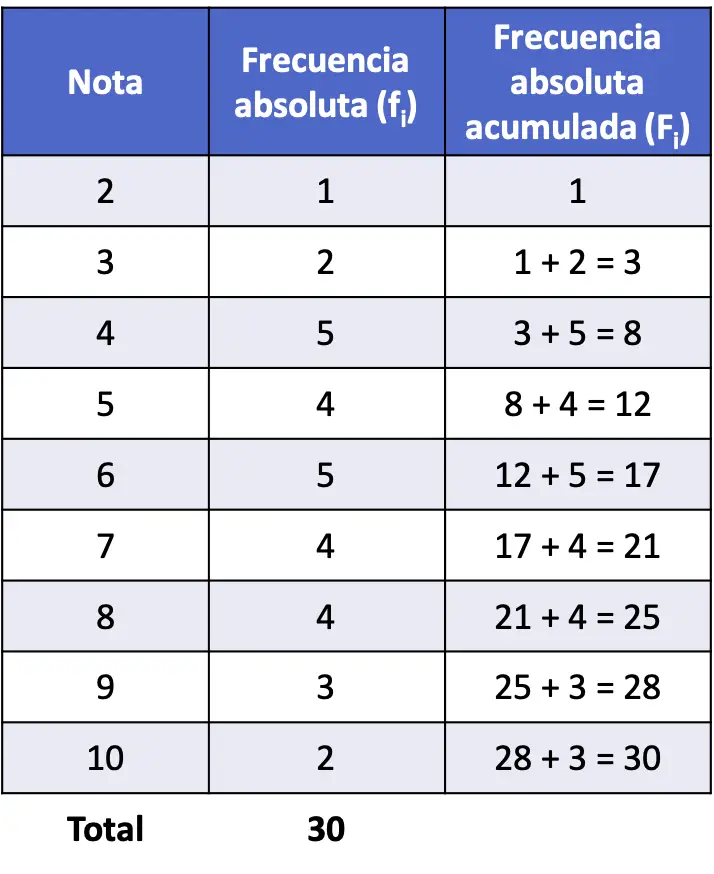
La frecuencia absoluta acumulada del último valor siempre coincide con el número total de datos, puedes utilizar este truco para comprobar que los cálculos están bien.
Luego tenemos que determinar la frecuencia relativa, que se calcula dividiendo la frecuencia absoluta entre el número total de datos (30):
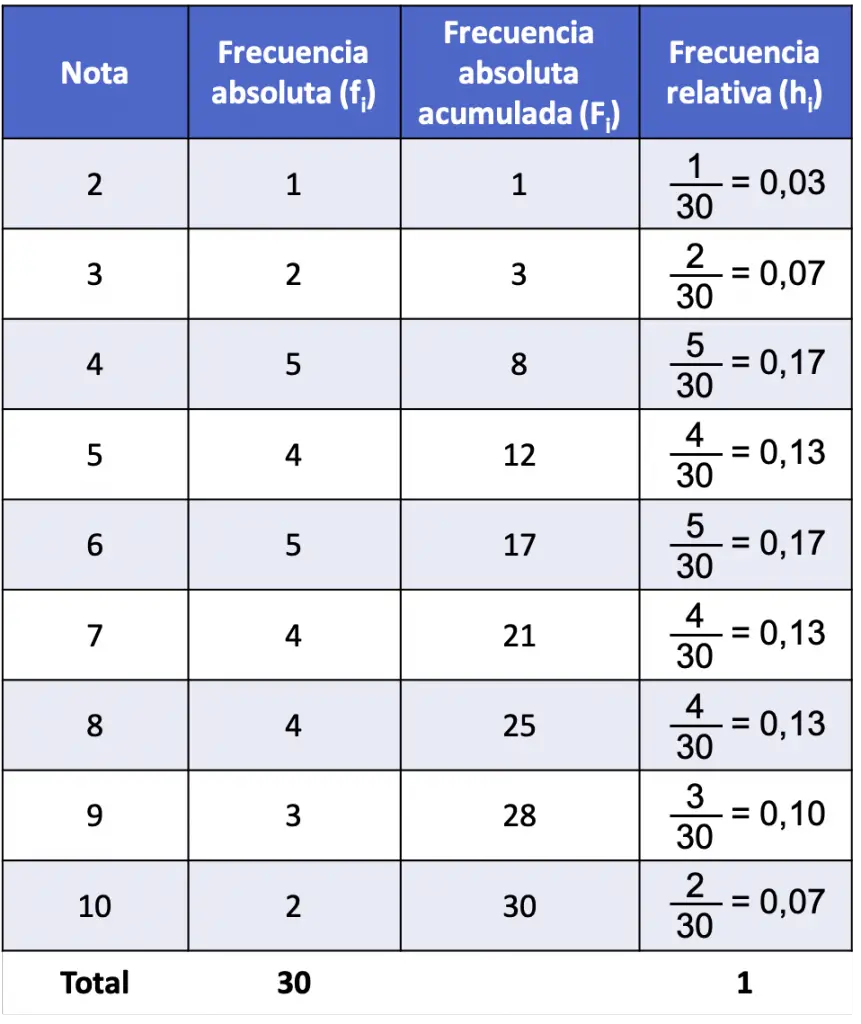
Ten presente que la suma de todas las frecuencias relativas siempre da como resultado 1, de lo contrario, significa que algún cálculo de la distribución de frecuencias está mal.
Por último, solo nos queda sacar la frecuencia relativa acumulada. Para ello, tenemos que sumar la frecuencia relativa del valor en cuestión más todas las frecuencias relativas anteriores o, lo que es lo mismo, la frecuencia relativa acumulada anterior:
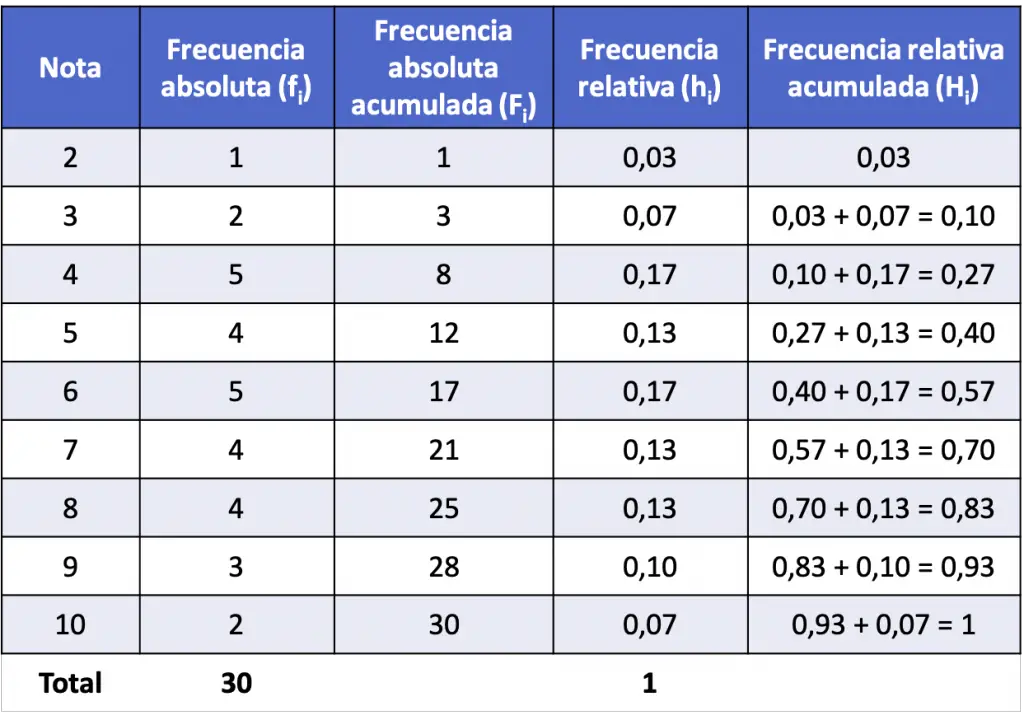
En definitiva, la distribución de frecuencias con todas las frecuencias de los datos del problema es la siguiente:
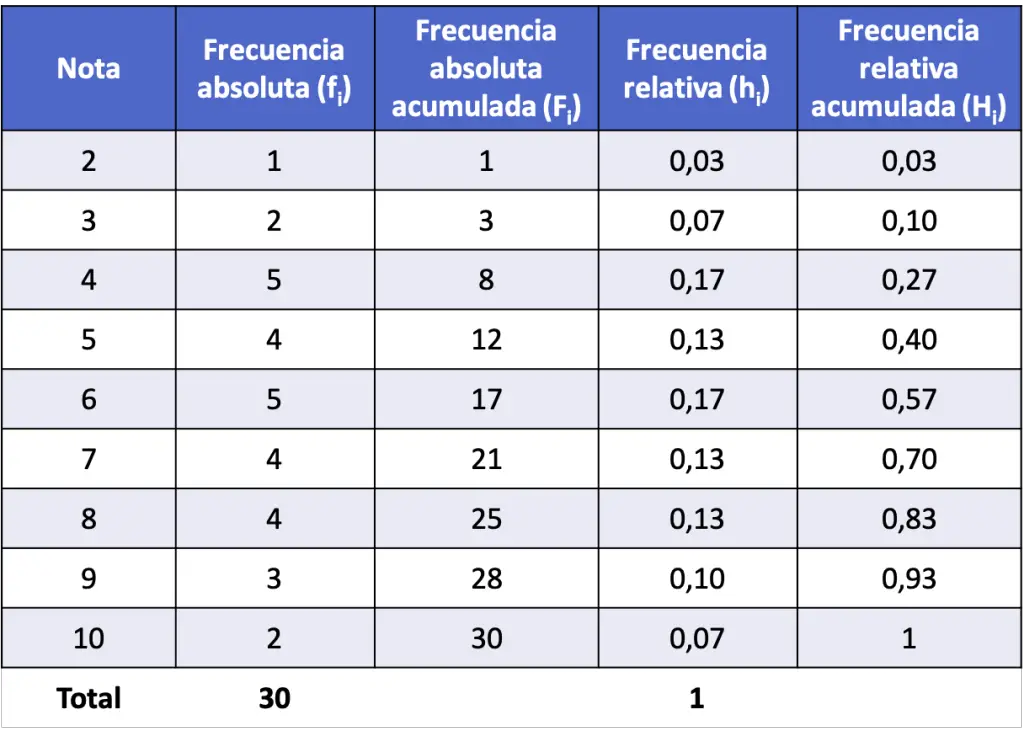
Distribución de frecuencias para datos agrupados
Para hacer una distribución de frecuencias para datos agrupados en intervalos, la única diferencia es que primero se deben agrupar el conjunto de datos en diferentes intervalos, pero el resto de cálculos se hacen de la misma manera que en una distribución de frecuencias sin agrupar los datos.
A modo de ejemplo, seguidamente se resuelve un problema sobre la construcción de una distribución de frecuencias para datos agrupados.
- Se ha medido la altura a 20 personas y se han obtenido los resultados anotados abajo. Elabora una distribución de frecuencias separando los datos en intervalos.
![]()
![]()
Los datos de esta muestra siguen una distribución continua, ya que los números pueden ser decimales y por tanto pueden tomar cualquier valor. En consecuencia, haremos la distribución de frecuencias agrupando los datos en intervalos.
Aunque hay varias reglas matemáticas para crear los intervalos de una muestra, en este caso sencillamente haremos intervalos con una amplitud de 10 décimas.
Así pues, después de calcular todos los tipos de frecuencias para cada intervalo (el procedimiento es el mismo que en el ejemplo de arriba), la distribución de frecuencias con los datos agrupados en intervalos queda de la siguiente manera:
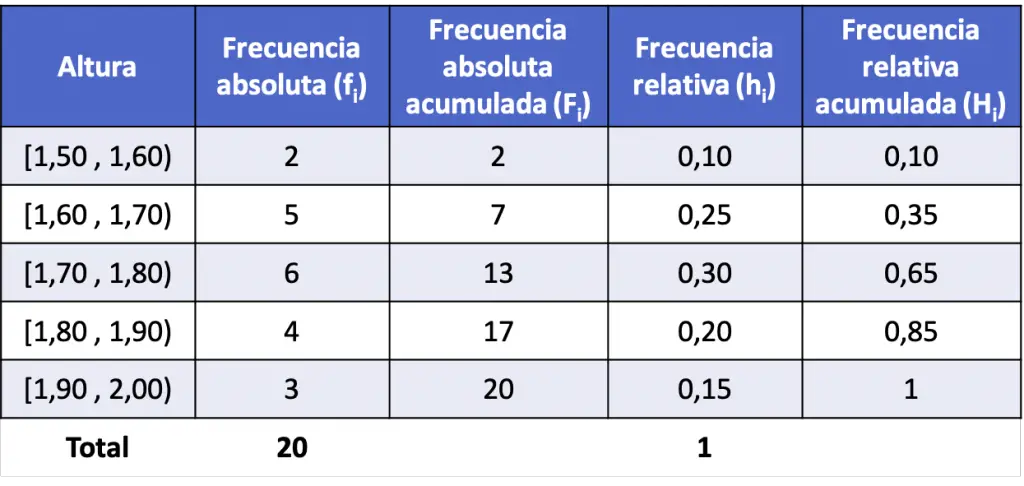
Ejercicios resueltos de distribuciones de frecuencias
Ejercicio 1
Se ha preguntado a 20 personas cuántas veces van al cine al mes y estos han sido los resultados:
![]()
![]()
Realiza una distribución de frecuencias con la muestra de datos obtenida.
La distribución de frecuencias con los cálculos de todos los tipos de frecuencias es la siguiente:
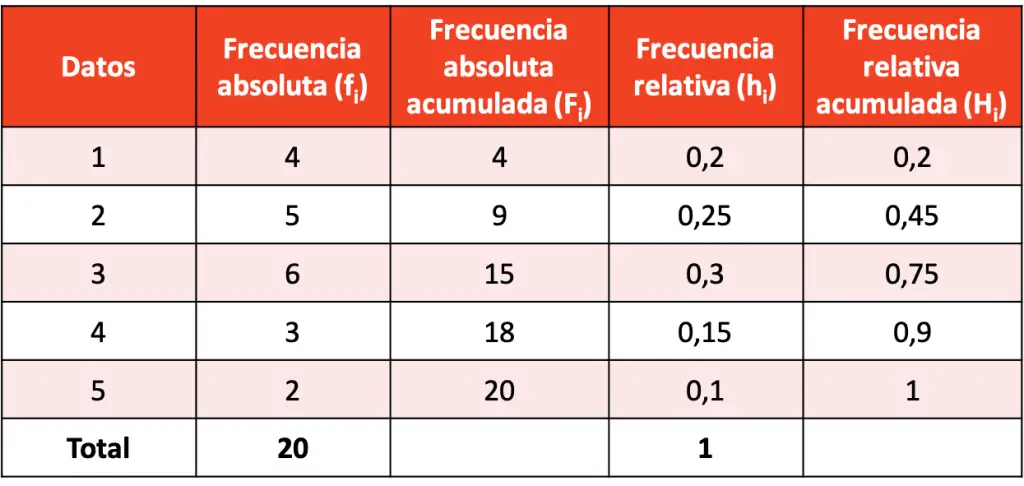
Ejercicio 2
Se quiere hacer un estudio estadístico sobre el peso de los trabajadores de una empresa con 36 empleados. Estos son los pesos de los trabajadores expresados en kilogramos:
![]()
![]()
![]()
![]()
![]()
![]()
Construye una distribución de frecuencias con datos agrupados haciendo intervalos de 5 unidades y que el primer intervalo sea [55,60).
La solución del ejercicio es la siguiente distribución de frecuencias:
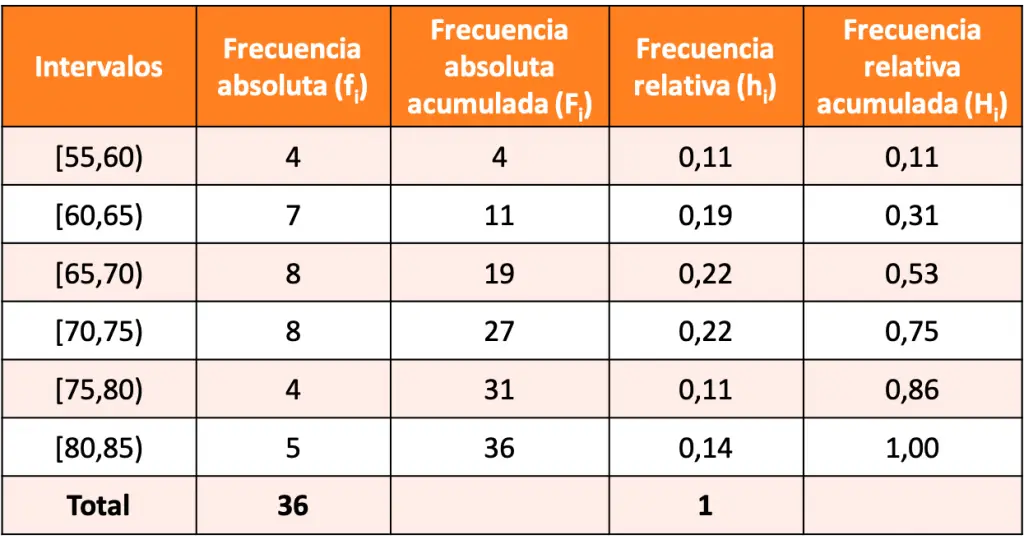

Agradezco el esfuerzo en desarrollar este tipo de información tan a detalle y fácil de comprender, recomendaré su sitio, saludos.
¡Muchas gracias Enrique! ¡Me alegro de que te guste!
MAGNFICO!SIMPLE Y SENCILLO PARA ENTENDER..FELICIDADES
¡Muchas gracias Ismael!